Примеры для самостоятельного решения.
Найти изображения следующих оригиналов:
1) 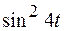 ; ; | 2) 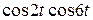 ; ; | 3) 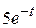 ; ; | 4) 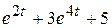 |
Ответы: 1) 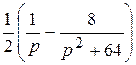 ; ; | 2) 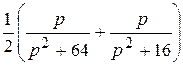 ; ; | 3) 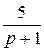 | |
4) 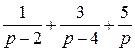 |
Применение теоремы запаздывания для нахождения изображений запаздывающих процессов.
Теорема.Если 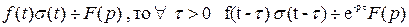 .
.
Т.о., запаздывание оригинала на время 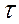 соответствует умножению изображения на
соответствует умножению изображения на 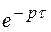 .
.
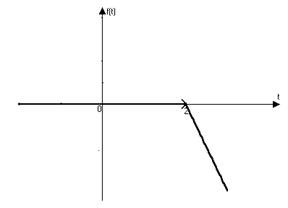
Примеры 1-4. Построить графики и найти изображения следующих оригиналов: 1) 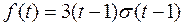
Решение.
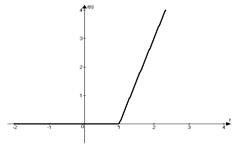 |
Построим график
 Так как
Так как 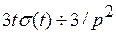 , то
, то 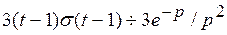 ;
;
2) 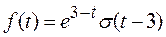
Решение.
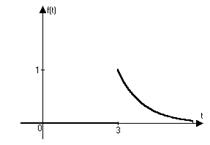 |
Так как
 , то
, то 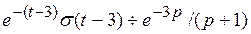 ;
; 3) 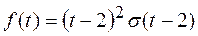

Решение. Так как 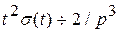 , то
, то 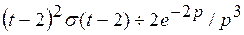 ;
;
4) 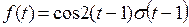
Решение.
Т.к. 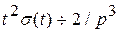
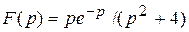
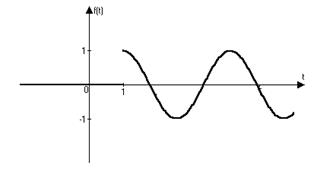
;
Чтобы воспользоваться теоремой запаздывания нужно преобразовать оригинал к удобному для получения изображения виду, т.е.
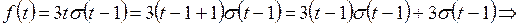
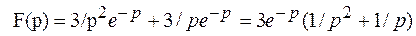 ;
;
5) 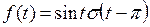
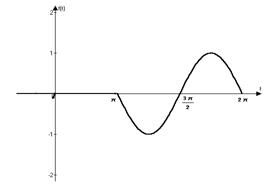 |
Решение. Преобразуем оригинал:
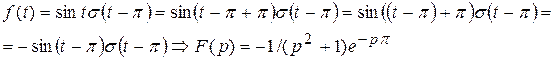
Вопросы для самопроверки
1. Сформулируйте теорему запаздывания.
Примеры 1-4 для самостоятельного решения.
Построить графики и найти изображения следующих оригиналов:
1) 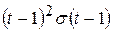 ; ; | 2) 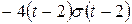 ; ; | 3) 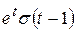 ; ; |
4) 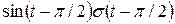 |
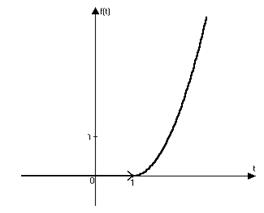 |
Ответы:
1) | 2) |
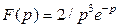 | 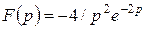 |
| 3) | 4) |

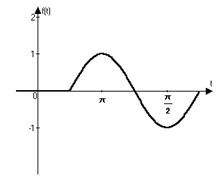 |
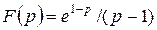 | 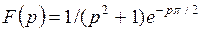 |
Изображение кусочно - непрерывных функций.
Примеры. Построить график оригинала, записать его одним аналитическим выражением, найти изображение.
1) 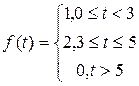
Решение.
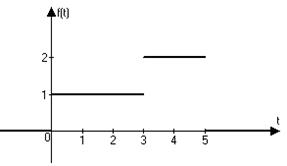
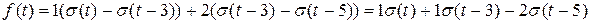
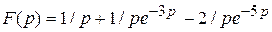 ;
;
2) 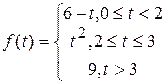
Решение:
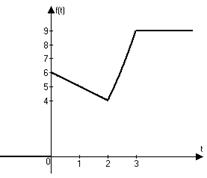
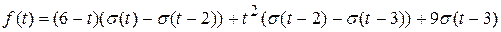
Приведём оригинал к виду, удобному для получения изображения.
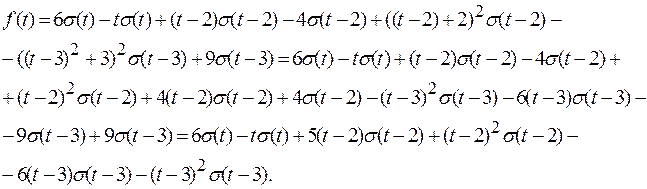 Применяя свойства линейности и теорему запаздывания , получаем
Применяя свойства линейности и теорему запаздывания , получаем
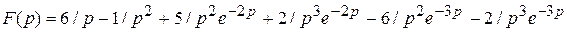 ;
;
3) 
Решение:
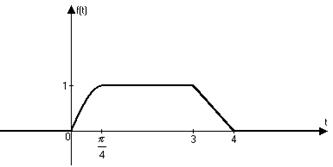
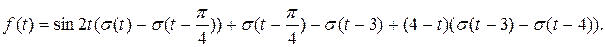 Приведём оригинал к виду, удобному для получения изображения
Приведём оригинал к виду, удобному для получения изображения
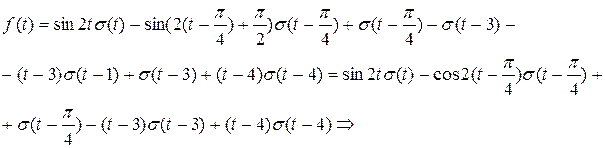
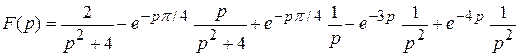 .
.
Примеры 1-4 для самостоятельного решения.
Построить график, записать одним аналитическим выражением, найти изображение.
1) 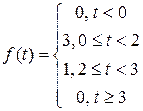 ; ; | 2) 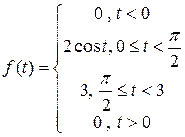 ; ; |
3) 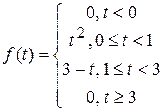 ; ; | 4) 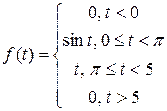 . . |
Ответы:
1) 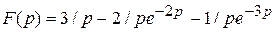 ;
;
2) 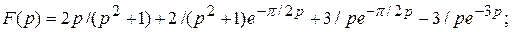
3) 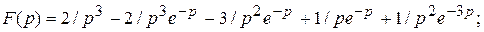
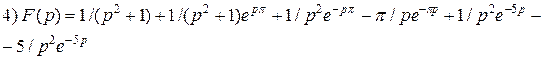
Примеры 5-6. По графику записать оригинал, представить его одним аналитическим выражением, найти изображение.
5)
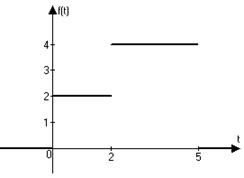
Решение:
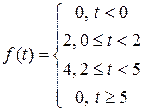
Приведем к виду, удобному для применения свойства линейности и теоремы запаздывания, получаем
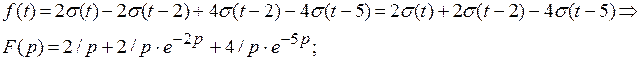 6)
6)
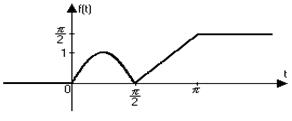
Оригинал: 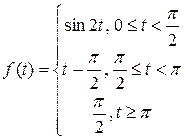
Запишем оригинал одним аналитическим выражением, чтобы применить теорему запаздывания
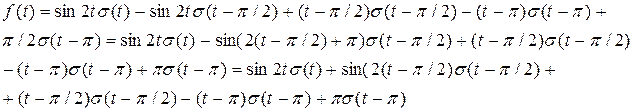 Тогда
Тогда
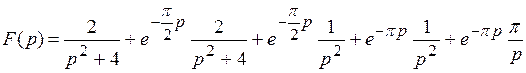 ;
;
Примеры для самостоятельного решения.
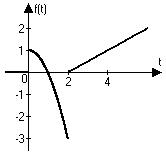
По графику найти оригинал, представить его одним аналитическим выражением и найти изображение.
1) 2)
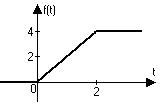
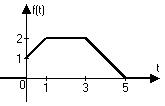
3) 4)
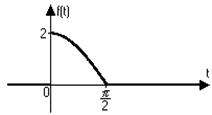
Ответы:
1) 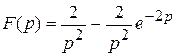 ; 2)
; 2) 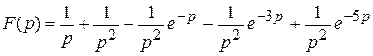 ;
;
3) 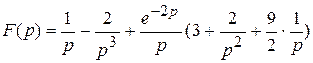 ; 4)
; 4) 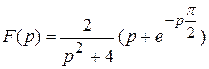
Применение теорем о дифференцировании оригинала и изображения для нахождения изображений.
Теорема о дифференцировании оригинала.
Если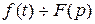 , то
, то 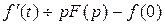 , где
, где 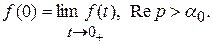
Следствие. Если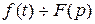 , то
, то 
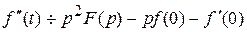 ,
,
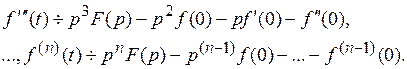
Пример1.
Найти изображение 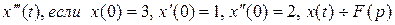
Решение.
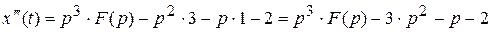
Теорема о дифференцировании изображения.
Если 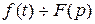 , то
, то  .
.
Следствие. Если 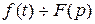 , то
, то 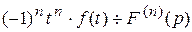 .
.
Пример 2. Найти изображение 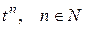 .
.
Решение:
Т. к. 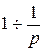 , то
, то 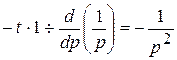 , т.е.
, т.е. 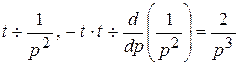 , т.е.
, т.е. 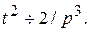 Так как
Так как 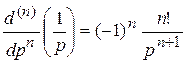 , то
, то 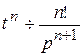 .
.
Пример 3. Найти изображение 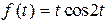 .
.
Решение:
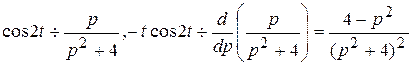 , т.е.
, т.е. 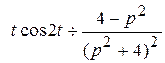 .
.
Пример 4. Найти изображение 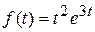 .
.
Решение:
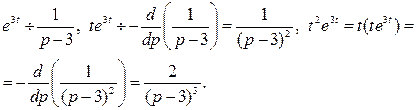
Вопросы для самопроверки
1. Сформулируйте теорему о дифференцировании оригинала
2. Сформулируйте теорему о дифференцировании изображения
Примеры 1-6 для самостоятельного решения.
Найти изображение с помощью теорем о дифференцировании оригинала и изображения.
1) 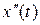 , если
, если 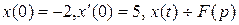 ;
;
2) 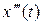 , если
, если 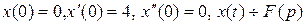 ;
;
3) 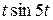 ; 4)
; 4) 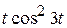 ; 5)
; 5) 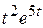 ;6)
;6) 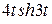 ;
;
Ответы: 1) 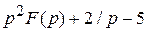 ; 2)
; 2) 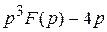 ; 3)
; 3) 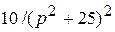 ;
;
4) 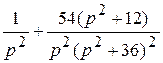 ; 5)
; 5) 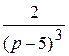 ; 6)
; 6) 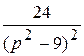 .
.
Изображение интеграла от оригинала.