Задача на подобие треугольников

Отрезки и прямые

Теоретический материл, необходимый для решения задач.

Когда две прямые пересекаются в одной точке, то они образуют четыре угла. При этом они попарно являются вертикальными и смежными.

Вертикальные углы - это углы, которые образованы пересечением двух прямых и не являются прилегающими. Они имеют общую вершину и равны между собой.

Смежные углы - это углы, образованные пересечением двух прямых, имеющие общую сторону, общую вершину и дополняющие друг друга до 180 градусов. Две другие стороны образуют собой прямую линию. Сумма смежных углов равна 180 градусов.

Отрезки в координатной плоскости

В этом уроке содержатся задачи по геометрии, в которых необходимо найти координаты различных точек отрезков, находящихся на координатной плоскости. Приведены решения задач, которые могут вызывать у школьников затруднения при решении.

Задачи об отрезках на координатной плоскости

Задача.
Расстояние между точками A(m;-3) и B(1;5) равно 10. Найдите значение m.

Решение.
Примечание. Вместо знака квадратного корня далее по тексту использовано выражение sqrt(), что следует читать как квадратный корень, подкоренное выражение которого указано в скобках.

Найдем расстояние между этими точками согласно формуле длины отрезка.
sqrt( (x₁-x₂)²+(y₁-y₂)² ),
подставим значения соответствующих координат точек отрезка
sqrt( (m-1)²+(-3-5)² ),
согласно условию, длина отрезка равна 10, получаем
sqrt( (m-1)²+(-3-5)² ) = 10
(m-1)²+(-3-5)² = 100
m²- 2m + 65 = 100
m²- 2m - 35 = 0
решаем полученное квадратное уравнение
D = 144
x₁=7
x₂=-5
Ответ: Возможные значения m 7 и -5

Задача.
Найдите координаты точки, лежащей на оси y и равноудаленной от точек с координатами A(-2;3) и B(6;1).

Решение.
Примечание. Вместо знака квадратного корня далее по тексту использовано выражение sqrt(), что следует читать как квадратный корень, подкоренное выражение которого указано в скобках.

Обозначим искомую точку как С. Поскольку известно, что искомая точка равноудалена от заданных точек А и В, то она находится от заданных координат точек на одном и том же расстоянии. Это означает, что длина отрезка BC равна длине отрезка AC.

BC = AC

Найдем расстояние между этими точками согласно формуле длины отрезка.
sqrt( (x₁-x₂)²+(y₁-y₂)² ),

Учтем, что, поскольку искомая точка С лежит на оси y, то для точки С координата x=0.
AC = sqrt( (-2 - 0)² +(3 - y)² )
BC = sqrt( (0 - 6)² +(y - 1)² )

Поскольку AC=BC, приравняем выражения
sqrt( (-2 - 0)² +(3 - y)² ) = sqrt( (0 - 6)² +(y - 1)² )
(-2 - 0)² +(3 - y)² = (0 - 6)² +(y - 1)²
4 + 9 - 6y + y² = 36 + y² - 2y + 1
- 6y + 2y + y²- y² =36 + 1 - 4 - 9
- 4y = 24
y = -6

Ответ: Координаты искомой точки (0;-6)

Прямые на координатной плоскости

Задача.

Докажите, что точки A(-2;-3), B(2;1) и C(7;6) лежат на одной прямой. Какая из точек лежит между двумя другими?

Решение.

Формула уравнения прямой, проходящих через две точки (x₁;y₁) и (x₂;y₂) имеет вид
( y - y₁ ) / ( y₂ - y₁ ) = (x - x₁) / (x₂-x₁)

Выведем уравнение прямой AB. Применим координаты точек A(-2;-3), B(2;1). Получим:

( y - (-3) ) / ( 1 - (-3) ) = ( x - (-2) ) / ( 2 - (-2))
( y + 3 ) / 4 = ( x + 2 ) / 4
y + 3 = x + 2
y = x - 1

Таким образом, полученному уравнению соответствуют все точки, лежащие на данной прямой. Подставив в уравнение, значение х точки С, получим:

y = 7 - 1 = 6

То есть прямая проходит через точку C(7;6)

Вывод: Все точки A, B, C лежат на одной прямой

Векторы

Примечание. Это часть урока с задачами по геометрии (раздел векторы). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение.

Задача.
Найдите косинусы углов треугольника ABC, если его стороны заданы векторами A(-3;2), B(5;3), C(-4;-3). Определите вид треугольника.

Решение.
Косинус угла между двумя прямыми, на которых лежат векторы равен
|a₁b₁+a₂b₂| / ( sqrt(a₁+a₂) + sqrt(b₁+b₂))

вычислим значения:
cos AB = -(-3*5 + 2 * 3) / ( √13 √34) ≈ 0.428
cos BC = -(5*(-4) + 3 * (-3)) / ( 5 √34) ≈ 0.995
cos AC = -(-3*(-4) + 2 * (-3)) / ( 5 √13 ) ≈ -0.333

Соответственно углы равны приблизительно 64,7 , 5,7 и 109,6 треугольник тупоугольный

Пересекающиеся прямые

Примечание. Текст задачи взят из вопросов посетителей сайта.

Задача.

Один із кутів, що утворилися при перетині двох прямих, дорівнює 40 градусів. Знайдіть інші кути.

Один из углов, которые получились при пересечении двух прямых, равен 40 градусам. Найдите остальные углы.

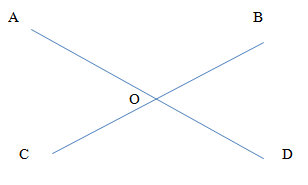
Решение.
Пусть прямые AD и BC пересекаются в O, при этом величина угла AOC по условию задачи равна 40 градусам.

Углы AOC и BOD - вертикальные, соответственно, по свойству вертикальных углов, они равны. Поэтому ∠AOC = ∠BOD = 40 градусов

Углы AOC и DOC - смежные. Согласно основному свойству смежных углов, их сумма равна 180 градусов.
Соответственно, ∠AOC + ∠DOC = 180 градусов, откуда
∠DOC = 180 - 40 = 120 градусов

Углы DOC и AOD - вертикальные, соответственно, ∠DOC = ∠AOD = 120 градусов

Ответ: углы, образованные пересечением двух прямых равны 40, 120, 40 и 120 градусов.

Окружности

Окружность

Примечание. В данном уроке изложены задачи по геометрии об окружности. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Почти наверняка курс будет дополнен.

Задача.
Определить радиус окружности, если она длиннее своего диаметра на 107 сантиметров

Решение.
Обозначим длину окружности как C, а диаметр как D.
Таким образом C - D = 107

Длина окружности равна С = 2πR = πD , поэтому
πD - D = 107
D ( π - 1 ) = 107
D = 107 / ( π - 1 ) ≈ 49,96 см

Откуда радиус окружности R = D / 2 = 107 / 2( π - 1 ) ≈ 24,98 см

Ответ: 107 / 2( π - 1 ) ≈ 24,98 см

Задача.
Разность между радиусами окружностей, одна из которых описана около правильного треугольника, а вторая - вписана, равна m. Определить стороны этого треугольника.

Решение.
Радиус вписанной окружности правильного треугольника, выраженный через его сторону равен
r = √3/6 a
Радиус описанной окружности правильного треугольника, выраженный через его сторону равен
R = √3/3 a

Поскольку R - r = m, то

√3/3 a - √3/6 a = m
a ( √3/3 - √3/6 ) = m
a √3/6 = m
a = 6m / √3

Ответ: 6m / √3

См. также задачи про окружность, описанную вокруг треугольника.

Хорды на окружности

Задача.
Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ.

Решение.

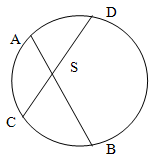
Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x

Согласно свойству хорд AS x SB = CS x SD, тогда

2х * 3х = 5 * 12
6х² = 60
х² = 10
x = √10

Откуда
AB = AS + SB
AB = 2√10 + 3√10= 5√10

Ответ: 5√10

Задача.
Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника.

Решение.
Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг).
Поскольку градусная мера окружности равна 360 градусам, то

3,5х + 5,5х + 3х = 360
12х = 360
х = 30

Откуда градусные величины центральных углов равны:
3 * 30 = 90
3,5 *30 = 105
5,5 *30 = 165

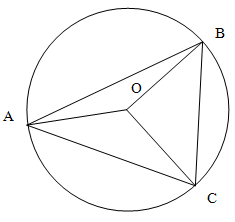
Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
Откуда углы треугольника равны:
90 / 2 = 45
105 / 2 = 52,5
165 / 2 = 82,5

Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;

Треугольники

Задачи по геометрии про треугольники и их свойства. Рассматриваются задачи по геометрии, решение которых вызывает у школьников трудности. Основное внимание уделяется принципу решения подобных задач.

Высота

Задача на подобие треугольников.

В прямоугольном треугольнике ABC (угол C = 90⁰) проведена высота CD. Определите CD, если AD = 9 см, BD = 16 см

Решение.

Треугольники ABC, ACD и CBD подобны между собой . Это непосредственно следует из второго признака подобия (равенство углов в этих треугольниках очевидно).

Прямоугольные треугольники - единственный вид треугольников, которые можно разрезать на два треугольника, подобных между собой и исходному треугольнику.

Обозначения этих трех треугольников в таком порядке следования вершин: ABC, ACD, CBD. Тем самым мы одновременно показываем и соответствие вершин. (Вершине A треугольника ABC соответствует также вершина A треугольника ACD и вершина C треугольника CBD и т. д.)

Треугольники ABC и CBD подобны. Значит:

AD/DC = DC/BD, то есть

DC²=AD*BD

DC²=9*16

DC=12 см