Другие характеристики вариационных рядов.
Сделаем краткий обзор, еще не рассмотренных характеристик вариационного ряда. Определим эти характеристики для дискретного ряда, зная, что для получения аналогичных характеристик интервального ряда нужно значения вариантов заменить серединами интервалов.
Начальным моментом 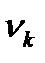 порядка k дискретного вариационного ряда называется средняя арифметическая k -ых степеней вариантов, т.е.
порядка k дискретного вариационного ряда называется средняя арифметическая k -ых степеней вариантов, т.е.
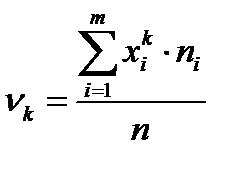 (5.16)
(5.16)
Очевидно, что начальный момент нулевого порядка равен 1. Начальный момент первого порядка является средней арифметической, т.е. 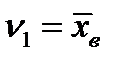 .
.
Центральным моментом 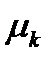 порядка k дискретного вариационного ряда называется средняя арифметическая k -ых степеней отклонений вариантов от их средней выборочной, т.е.
порядка k дискретного вариационного ряда называется средняя арифметическая k -ых степеней отклонений вариантов от их средней выборочной, т.е.
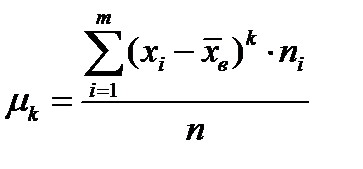 (5.17)
(5.17)
Очевидно, что центральный момент нулевого порядка равен 1. Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии, т.е. 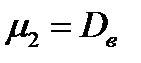 .
.
Заменив в формуле (5.16) и (5.17) значение вариантов на середины интервалов интервального ряда, получим формулу для начальных и центральных моментов интервального ряда.
Нетрудно выразить центральные моменты через обычные и получить следующие формулы:
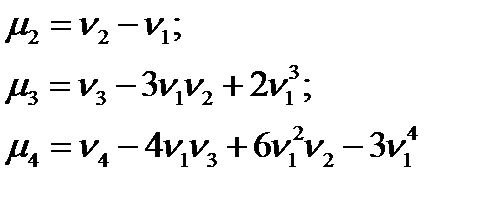
и т.д.
Начальные и центральные моменты обладают свойствами, аналогичными свойствам средней арифметической и дисперсии, поэтому для их нахождения можно также использовать условные варианты, что позволит существенно упростить расчеты.
Моменты вариационных рядов позволяют не только описать среднее значение и рассеивание вариантов вариационного ряда, но и найти другие особенности распределения.
Для оценки отклонения статистического распределения (в виде вариационного ряда) от нормального распределения соответствующей случайной величины, используют понятия коэффициентов асимметрии и эксцесса. Смысловое содержание этих характеристик аналогично смыслу асимметрии и эксцесса теоретического распределения случайной величины.
Коэффициентом асимметрии 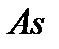 (или просто асимметрией) вариационного ряда называется число, определяемое по формуле:
(или просто асимметрией) вариационного ряда называется число, определяемое по формуле:
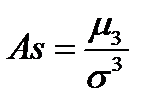 .
.
Асимметрия показывает, насколько симметричным является распределение вариационного ряда.
Если  =0, то распределение имеет симметричную форму. Это означает, что варианты, равноудаленные в разные стороны от
=0, то распределение имеет симметричную форму. Это означает, что варианты, равноудаленные в разные стороны от 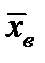 , имеют одинаковые частоты. Кроме этого, очевидно, что полигон распределения частот будет представлять симметричную, относительно прямой
, имеют одинаковые частоты. Кроме этого, очевидно, что полигон распределения частот будет представлять симметричную, относительно прямой 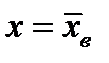 , фигуру.
, фигуру.
Если  > 0, то говорят, что распределение имеет положительную (или правостороннюю) асимметрию. В этом случае полигон асимметричен и правая его ветвь, начиная с вершины, имеет более пологий вид, чем левая.
> 0, то говорят, что распределение имеет положительную (или правостороннюю) асимметрию. В этом случае полигон асимметричен и правая его ветвь, начиная с вершины, имеет более пологий вид, чем левая.
Если 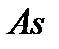 < 0, то говорят, что распределение имеет отрицательную (или левостороннюю) асимметрию. В этом случае полигон также асимметричен и левая его ветвь, начиная с вершины, имеет более пологий вид, чем правая.
< 0, то говорят, что распределение имеет отрицательную (или левостороннюю) асимметрию. В этом случае полигон также асимметричен и левая его ветвь, начиная с вершины, имеет более пологий вид, чем правая.
Коэффициентом эксцесса 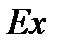 (или просто эксцессом) вариационного ряда называется число, определяемое по формуле:
(или просто эксцессом) вариационного ряда называется число, определяемое по формуле:
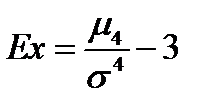 .
.
Эксцесс определяет «крутость» вариационного ряда по сравнению с соответствующим нормальным распределением.
Если 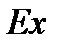 = 0, то распределение считают нормальным.
= 0, то распределение считают нормальным.
Если  > 0, то полигон данного распределения более крутой по сравнению с кривой нормального распределения.
> 0, то полигон данного распределения более крутой по сравнению с кривой нормального распределения.
Если 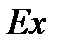 < 0, то полигон данного распределения более пологий по сравнению с кривой нормального распределения.
< 0, то полигон данного распределения более пологий по сравнению с кривой нормального распределения.
