Дәріс. Туындының көмегімен функцияларды зерттеу және графигін салу
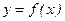 функциясы
функциясы  аралығында берілсін. Егер кез келген
аралығында берілсін. Егер кез келген 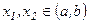 үшін
үшін 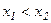 теңсіздігінен
теңсіздігінен 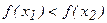 (
( 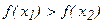 ) теңсіздігі шығатын болса, онда
) теңсіздігі шығатын болса, онда 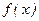 функциясы
функциясы  аралығында өседі (кемиді) дейді.
аралығында өседі (кемиді) дейді.
Теорема. Егер  аралығында дифференциалданатын
аралығында дифференциалданатын 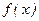 функциясының туындысы осы аралықта оң (теріс) болса, онда ол осы аралықта өседі (кемиді). Демек, өсу немесе кему интервалында функцияның туындысы таңбасын өзгертпейді.
функциясының туындысы осы аралықта оң (теріс) болса, онда ол осы аралықта өседі (кемиді). Демек, өсу немесе кему интервалында функцияның туындысы таңбасын өзгертпейді.
1-мысал. 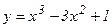 функцияның өсу және кему аралықтарын табу керек. Ол үшін функция туындысының таңбасының тұрақтылық интервалдарын анықтаймыз
функцияның өсу және кему аралықтарын табу керек. Ол үшін функция туындысының таңбасының тұрақтылық интервалдарын анықтаймыз 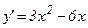 . Бұл квадрат үшмүшеліктің түбірлері x1=0, x2=2. Сондықтан, егер
. Бұл квадрат үшмүшеліктің түбірлері x1=0, x2=2. Сондықтан, егер 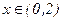 аралығында
аралығында 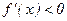 , демек
, демек 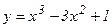 функциясы бұл аралықта кемиді. Ал
функциясы бұл аралықта кемиді. Ал 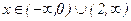 аралықтарында f'(x)>0, демек бұл аралықтарда функция өседі.
аралықтарында f'(x)>0, демек бұл аралықтарда функция өседі.
Теорема (экстремумның қажетті шарты).Егер дифференциалданатын 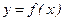 функциясының
функциясының 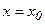 нүктесінде экстремумы бар болса, онда сол нүктеде
нүктесінде экстремумы бар болса, онда сол нүктеде 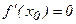 болады. Осы теоремадан мынадай қорытындыға келеміз: егер
болады. Осы теоремадан мынадай қорытындыға келеміз: егер 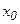 нүктесінде функцияның экстремумы бар болса, онда ол нүктеде оның туындысы нөлге тең, не ол нүктеде туындысы болмауы мүмкін. Кері тұжырым әрқашан орындала бермейді. Мысалы,
нүктесінде функцияның экстремумы бар болса, онда ол нүктеде оның туындысы нөлге тең, не ол нүктеде туындысы болмауы мүмкін. Кері тұжырым әрқашан орындала бермейді. Мысалы, 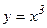 функциясының x0=0 нүктесінде туындысы
функциясының x0=0 нүктесінде туындысы 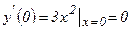 , ал бірақ ол нүктеде функция не максимум, не минимум қабылдамайды.
, ал бірақ ол нүктеде функция не максимум, не минимум қабылдамайды. 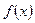 функциясының туындысы нөлге айналатын немесе тіпті болмайтын нүктелерді күдікті нүктелер немесе «кризистік» нүктелер деп атайды. Функцияның экстремумын осы күдікті нүктелердің арасынан іздеу керек.
функциясының туындысы нөлге айналатын немесе тіпті болмайтын нүктелерді күдікті нүктелер немесе «кризистік» нүктелер деп атайды. Функцияның экстремумын осы күдікті нүктелердің арасынан іздеу керек.
Теорема (экстремумнің жеткілікті шарты). Егер 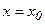 нүктесінде
нүктесінде 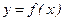 функциясының туындысы нөлге тең болса және
функциясының туындысы нөлге тең болса және 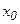 нүктесінен өткенде
нүктесінен өткенде 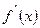 таңбасын өзгертсе, онда
таңбасын өзгертсе, онда 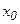 нүктесі экстремум нүктесі болады: 1) егер таңба «плюс»-тен «минус»-ке өзгерсе, онда
нүктесі экстремум нүктесі болады: 1) егер таңба «плюс»-тен «минус»-ке өзгерсе, онда 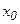 – максимум нүктесі; 2) егер таңба «минус»-тен «плюс»-ке өзгерсе, онда
– максимум нүктесі; 2) егер таңба «минус»-тен «плюс»-ке өзгерсе, онда 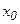 – минимум нүктесі болады.
– минимум нүктесі болады.
2-мысал. 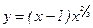 функцияны экстремумге зерттеп, өсу және кему аралықтарын анықтау керек. Функция туындысы
функцияны экстремумге зерттеп, өсу және кему аралықтарын анықтау керек. Функция туындысы 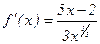 , осыдан
, осыдан 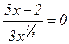 ,
, 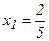 күдікті нүктесін табамыз.
күдікті нүктесін табамыз. 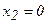 нүктесінде функцияның туындысы болмайды, сондықтан ол да күдікті нүкте. Интервалдар тәсілімен f '(x)-тің таңбаларын анықтаймыз. Функция
нүктесінде функцияның туындысы болмайды, сондықтан ол да күдікті нүкте. Интервалдар тәсілімен f '(x)-тің таңбаларын анықтаймыз. Функция 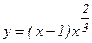 барлық нүктелерде үзіліссіз, жеткіліктілік шарт бойынша
барлық нүктелерде үзіліссіз, жеткіліктілік шарт бойынша 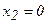 максимум нүктесі, ал
максимум нүктесі, ал 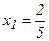 минимум нүктесі. (–¥, 0) және
минимум нүктесі. (–¥, 0) және 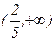 интервалдарда функция өседі, ал
интервалдарда функция өседі, ал 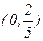 интервалда кемиді Зерттеу нәтижелерін таблицаға жазамыз:
интервалда кемиді Зерттеу нәтижелерін таблицаға жазамыз:
| x | (–¥,0) | (0, 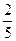 ) ) | 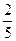 | ( 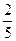 , +¥) , +¥) | |
| f '(x) | + | Туындысы жоқ | – | + | |
   f (x) f (x) | max | 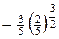 min min |
 |
Функцияның екінші ретті туындысы қолданылатын экстремумның тағы бір шартын келтірейік.
Теорема. 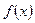 функциясының
функциясының 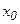 нүктесінде бірінші және екінші туындылары бар болсын. Егер
нүктесінде бірінші және екінші туындылары бар болсын. Егер 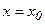 нүктесінде
нүктесінде 
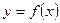 функциясының бірінші туындысы нөлге тең, яғни
функциясының бірінші туындысы нөлге тең, яғни 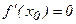 болса, ал екінші туындысы нөлден ерекше, яғни
болса, ал екінші туындысы нөлден ерекше, яғни 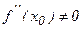 болса, онда
болса, онда 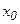 - экстремум нүктесі болады:
- экстремум нүктесі болады:
1) егер 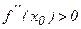 болса, онда
болса, онда 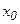 – минимум нүктесі;
– минимум нүктесі;
2) егер 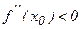 болса, онда
болса, онда 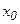 – максимум нүктесі болады.
– максимум нүктесі болады.
Функцияның кесіндідегі ең үлкен және ең кіші мәндері. Функция өзінің ең үлкен және ең кіші мәндерін экстремум нүктелерінде не кесіндісінің шеткі нүктелерінде қабылдауы мүмкін. Ең үлкен және ең кіші мәндерді табу үшін алдымен функцияның күдікті нүктелерін (не туынды нөлге тең, не туынды жоқ нүктелер) табу керек. Содан соң функцияның күдікті нүктелеріндегі және кесіндінің шеткі нүктелеріндегі мәндерін тауып, олардың ішінен ең үлкен және ең кіші мәндерді іздеу керек.
3-мысал. 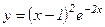 функциясының
функциясының 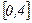 кесіндісіндегі ең үлкен жіне ең кіші мәндерін табу керек. Күдікті нүктелерді табамыз:
кесіндісіндегі ең үлкен жіне ең кіші мәндерін табу керек. Күдікті нүктелерді табамыз:
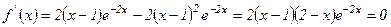 Осыдан
Осыдан 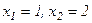 - күдікті нүктелер. Енді функцияның күдікті нүктелердегі және шеткі нүктелердегі мәндерін табамыз:
- күдікті нүктелер. Енді функцияның күдікті нүктелердегі және шеткі нүктелердегі мәндерін табамыз: 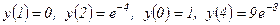 . Сонымен
. Сонымен  үлкен
үлкен 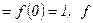 кіші
кіші  .
.
