Интерполяционный многочлен Лагранжа 3 страница

5. При вычисление объема цилиндра по формуле 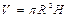, R = 36,7 cм и Н = 86,4 см. Сколько верных значащих цифр содержится в ответе?

6. Вычислите диагональ с прямоугольника, стороны которого а = 6,24 ± 0,005 см и b = 4,8 ± 0,05см. Сколько верных значащих цифр содержится в ответе?

7. С какой точностью надо измерить радиус круга,чтобы абсолютная погрешность площади круга не превышала 10 см²? Грубое приближенное значение R = 8,7 см.

Ответы

1) 3,7%; 2) 0,035; 3)1,2%; 4) 1%; 5) 364000 см³; верными являются цифры 3 и 6; 6) 7,9 ± 0,03; верными являются цифры 7 и 9; 6) до 0,2 см.

Самостоятельная работа

Вариант 1

1. Вычислите сумму 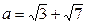, взяв приближенные значения корней с точностью до 0,001 найдите .

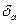2. Вычислите площадь параллелограмма, если а = 68,7, и h = 52,6. Укажите верные цифры ответа.

3. Найдите границу абсолютной погрешности произведения двух приближенных значений чисел а = 7,36 ± 0,004 и b = 8,61 ± 0,005.

4. Вычислите относительную погрешность .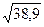

5. С какой точностью надо измерить радиус круга, чтобы относительная погрешность площади круга не превышала 0,5%? Грубое приближенное значения R = 8 м.

Вариант 2

1. Вычислите разность 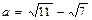с четырьмя значащими цифрами; найти .

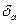2. Вычислите площадь прямоугольника, если а = 78,6, и h = 48,7. Укажите верные цифры ответа.

3. Вычислите 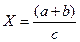, если а = 82,6, b = 93,8 и с = 61,9. Укажите границу абсолютной погрешности.

4. Вычислите относительную погрешность .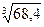

5. С какой точностью надо измерить сторону квадрата, чтобы относительная погрешность площади квадрата не превышала 1%? Грубое приближенное значения R = 9 м.

Ответы

I вариант. 1) 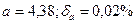; 2)3600; верные цифры 3 и 6; 3) 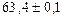; 4) 0,1%; 5) до 0,02 м.

II вариант.1) 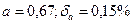; 2) 3800; верные цифры 3 и 8; 3) 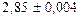; 4) 0,02%; 5) до 0,05.

Контрольные вопросы

1. Определение абсолютной и относительной погрешности.

2. Основные правила вычисления абслютной и относительной погрешностей.

Практическая работа № 8

Тема: «Приближенное решение уравнений. Погрешности приближенных значений чисел»

Основные вопросы: Постановка задачи. Корень уравнения. Отрезок изоляции корня. Отделение корней: графический способ, аналитический способ. Метод половинного деления при решении нелинейных уравнений. Критерий остановки метода.

Краткие теоретические сведения:

Пусть задана функция f(x) на 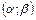- конечная или бесконечная, 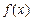непрерывна.

Рассмотрим уравнение f(x) = 0 (1)

Определение 1. Число 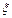называется корнем уравнения (1), если 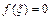, 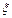- ноль функции f(х).

Будем считать только действительные корни.

Определение 2. Корень 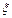уравнения (1) называется изолированным, если принадлежит отрезку 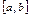в котором лежит корень 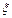, но в котором нет других корней уравнения (1). Отрезок 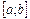- промежуток изоляции корня, 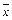- приближенный корень, 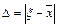- абсолютная погрешность абсолютного корня.

При решении уравнения (1) нужно знать приближенный корень с заданным приближением .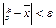

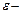степень точности, 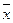- приближенный корень с точностью 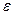, если выполняется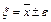

Определение 3. Корень 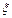- называется простым корнем, если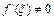

Будем рассматривать действительные, изолированные и простые корни уравнения (1)

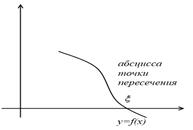
Рисунок 14

Вычисление корней

1. Нахождение промежутков изоляции всех корней уравнения (1).

2. Этап уточнения приближенного корня до нужной степени точности.

Рассмотрим первый этап:

Пусть функция f(x) задана на 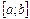и удовлетворяет условиям:

-непрерывна;

-на концах принимает разные знаки ,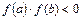

тогда на 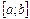уравнение (1) имеет по крайней мере один корень .

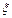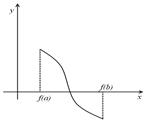
Рисунок 15

Теорема 2: Пусть f(x) на 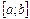удовлетворяет условие:

1. f(x)– непрерывна и дифференцируема;

2. ;

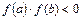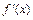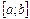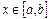
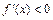
3. сохраняет знак , т.е. для любого 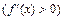возрастает (убывает), тогда 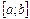промежуток изоляции корня .

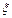Так мы выяснили область расположения всех решений уравнения (1).

Область расположения всех решений можем найти графическим способом.

Пусть найден отрезок [a; b], где f(a) f(b)<0, который содержит только один корень уравнения (1). Этот неизвестный корень обозначим буквой x. На II этапе по заданному числу e > 0 требуется на отрезке [a; b] найти приближенный корень 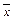с точностью e. Корень 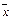будем искать итерационными методами.

Метод половинного деления

Метод половинного деления состоит в повторении (итерировании) следующей процедуры:

1) вычисление точки 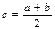, соответствующей середине отрезка [a; b];

2) вычисление значения функции f(c);

3) переход к отрезку 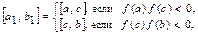удовлетворяющему всем свойствам отрезка [a; b], но вдвое меньшей длины.

В результате получаем последовательность {c_n} середин отрезков [a_n; b_n], длина которых неограниченно уменьшается.

«Правило останова»: вычисления прекращаются, когда впервые либо f(c_n)=0, либо 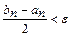, из последнего определяется число разбиений отрезка 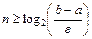. Искомый приближенный корень .

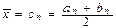Примеры решения задач

Пример 1. Определить корни уравнения .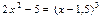

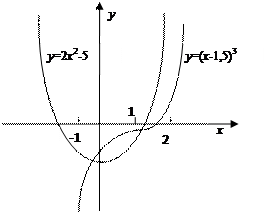
Рисунок 16

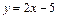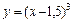Построив схематично графики функций и , убеждаемся, что они имеют три точки пересечения, абсциссы которых принадлежат отрезку [-1;6]. Следовательно, уравнение имеет три корня и эти корни принадлежат отрезку [-1;6].

Для отделения корней составим таблицу

х	-1
Знак f(x)	+	-	-	+	+	+	+	–

Следовательно, промежутки изоляции корней: [-1;0],[1;2] и [5;6].

Методом половинного деления уточнить промежуток изоляции [1;2] корня 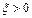уравнения с точностью до 0,01. Точкой 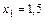делим отрезок [1;2] на два [1;1,5] и [1,5;2] и устанавливаем знак 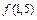. Значение 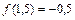. Так как 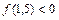, ,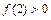то [1,5;2] – промежуток изоляции корня 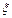. Проверяем критерий остановки: 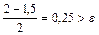. Снова находим 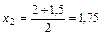и рассматриваем отрезки [1,5;1,75] и [1,75;2].

Так как 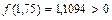, ,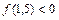то [1,5;1,75] – промежуток изоляции корня x. Проверяем критерий остановки: 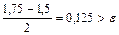.Сделаем еще один шаг 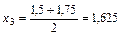и рассматриваем отрезки [1,5;1,625] и [1,625;1,75]. Так как 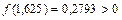, ,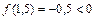то [1,5;1,625] – промежуток изоляции корня x. Проверяем критерий остановки: 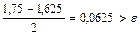. Сделаем еще один шаг 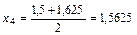и рассматриваем отрезки [1,5;1,5625] и [1,5625;1,625]. Так как 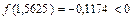, ,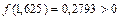то [1,5625;1,625] – промежуток изоляции корня x. Проверяем критерий остановки: 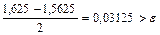. Сделаем еще один шаг 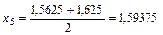и рассматриваем отрезки [1,5625;1,59375] и [1,59375;1,625]. Так как 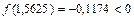, , 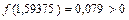то [1,5625;1,59375] – промежуток изоляции корня x. Проверяем критерий остановки: 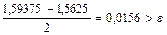. Сделаем еще один шаг 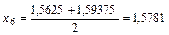и рассматриваем отрезки [1,5625;1,5781] и [1,5781;1,59375]. Так как 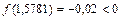, , 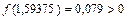то [1,5781;1,59375] – промежуток изоляции корня x. Проверяем критерий остановки: 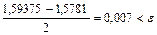, то вычисления можно остановить. В качестве грубого приближения корня можно взять:

.

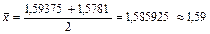Ответ: [1;2], .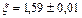

Порядок выполнения работы

1. Методом половинного деления уточнить корни уравнения 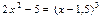на промежутках : [-1;0] и [5;6] с точностью до 0,01.

Контрольные вопросы

1. В чем заключается этап отделения корней при применении численных методов решения уравнений?

2. Какие свойства функции используются при нахождении промежутков изоляции корня?

3. Какие общие соображения можно использовать для оценки приближенных значений корня?

4. Какие цели преследуются при применении метода половинного деления?

Практическая работа № 9

Тема: «Приближенное решение уравнений: метод хорд и метод касательной»

Основные вопросы: Понятия метода последовательных приближений. Начальное приближение. Рекуррентная формула. Итерационная последовательность. Четыре случая выбора формулы и начального приближения. Сходимость итерационной последовательности. Оценка погрешности приближений. Комбинированный метод хорд и касательных.

Краткие теоретические сведения:Метод хорд при решении нелинейных уравнний состоит в построении последовательности {x_n} по итерационной формуле 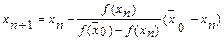, n=0,1,2,…,

начиная из начального приближения

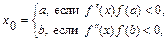(2)

а 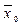– противоположный x₀ конец отрезка [a; b].

Условие сохранения знака 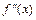на отрезке [a; b] является достаточным условием сходимости метода хорд. Если 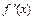сохраняет знак на отрезке [a; b] и выполняется условие

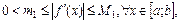
то имеет место следующее «правило останова»: вычисления прекращаются, когда впервые удовлетворяется неравенство

.

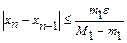Искомый приближенный корень .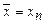

Метод Ньютона (метод касательных) состоит в построении последовательности 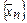(черта над x_n ставится для удобства изложения) по итерационной формуле

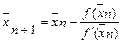, n=0,1,2,…,

начиная из начального приближения 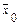, определенного в методе хорд (2).

Условие сохранения знаков 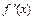и 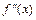на отрезке 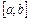является достаточным условием сходимости метода Ньютона. Если вторая производная 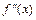ограничена на отрезке 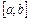и выполняется условие

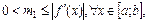
то имеет место следующее «правило останова»: вычисления прекращаются, когда впервые удовлетворяется неравенство |.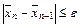

Искомый приближенный корень .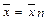

Комбинированный метод состоит в построении двух последовательносте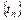й и 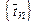путем поочередного применения итерационных формул

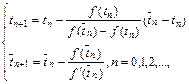
начиная из начальных приближений ,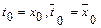

где 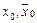– концы отрезка 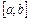, определенные в (2).

Поясним комбинированный метод на рисунке 17.

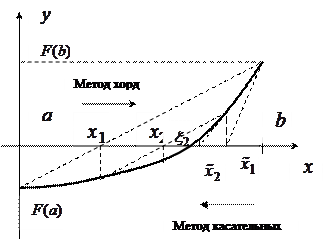
Рисунок 17

«Правило останова»: вычисления прекращаются, когда впервые удовлетворяется неравенство

| t_n - 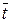_n| £ 2e.

Искомый приближенный корень

.

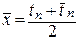Примеры решения задач

Для вычисления корня 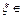[1,5;1,625] с точностью 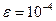применить метод хорд

Решение:

Проверим выполнение достаточных условий сходимости метода хорд:

1. [1,5;1,625] – промежуток изоляции;

2. 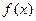– непрерывна всюду как многочлен

3.

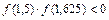
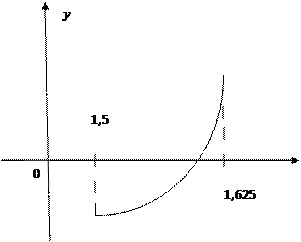
4. 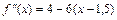для 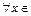[1,5;1,625] имеем .

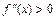Все условия выполнены

Схематично построим график функции:

Рисунок 18

Так как 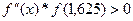,то неподвижным остается правый конец и метод хорд принимает вид: .

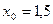Используем итерационную формулу для построения последовательности с начальным приближением X₀, составим таблицу

,

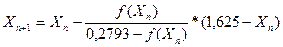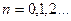
Для вычисления значений функций 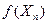используем таблицу:

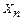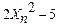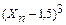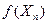1,5802	-0,00594	0,00052	-0,00646
1,58121	0,00046	0,00054	-0,00008

|Xn-1-Xn|	0,0802	0,00101	0,00001
(1)-(5)	1,5802	1,58121	1,58122
(2):(3)(4)	-0,0802	-0,00101	-0,00001
1,625- Xn	0,125	0,0448	0,04379
0,2793-f(Xn)	0,7793	0,28576	0,27938
f(Xn)	-0,5	-0,00646	-0,00008
Хn	1,5	1,5802	1,5802	1,5802
n

Проверим выполнение на [1,5;1,625] неравенства 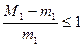(3)

Имеем 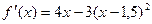Так как 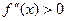на [1,5;1,625], то 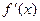функция возрастающая и значит:

, .

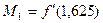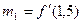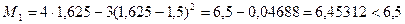
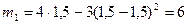
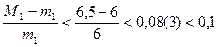
Ввиду выполнения неравенства (3) имеем оценку погрешности

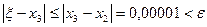
Вычисления прекращаются и 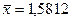–приближенное значение корня x с заданной точностью.

Ответ: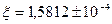

IV Для вычисления корня [1,5;1,625] применить метод Ньютона

Решение:

Помимо условий проверенных в задании IIIдля сходимости метода Ньютона требуется еще условие сохранения знака производной. Проверим это условие: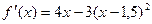

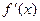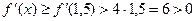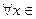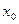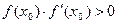
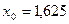
Так как возрастает на [1,5;1,625], то для [1,5;1,625] начальное приближение выберем из условия 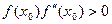Последовательные приближения вычисляются по формулам

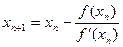, n=0,1,2…

Для вычисления составим таблицу:

n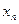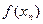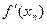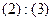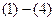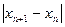
	1,625	0,2793	6,45312	0,04328	1,58172	0,04328
	1,58172	0,00313	6,30684	0,00049	1,58123	0,00049
	1,58123	0,00004	6,30512	0,00001	1,58122	0,00001
	1,58122

Вычисления прекращаются в виду достижения точности

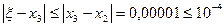
Ответ: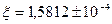

IV Для вычисления корни x с точностью не менее 10^-4 применить комбинаторный метод.

Решение:

Вычисления проводятся по формулам:

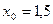
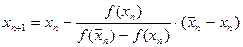, n=0,1,2…

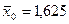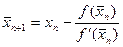, , n=0,1,2…

Составим таблицу для вычислений

f(Xn)		6,29534		(2)-(10)	1,57845	1,58122
(1)-(7)	1,5802	1,58123		(5):(9)	0,04655	-0,00277
(4):(6) (3)	-0,0802	-0,00103
(5)-(4)	0,7793	-0,01101
f(Xn)	0,2793	-0,01747
f(Xn)	-0,5	-0,00646
(2)–(1)	0,125	-0,00175	-0,00001
хn	1,625	1,57845	1,58122
хn 1	1,5	1,5802	1,58123
n