Определители, их свойства. Алгебраические дополнения
ТИПОВЫЕ РАСЧЕТЫ
Типовой расчет № 1
Векторы. Прямая. Кривые второго порядка
Во всех заданиях N – номер варианта.
Задание 1
На плоскости относительно некоторого базиса даны координаты трех векторов:
при N – четном: 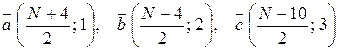 ;
;
при N – нечетном: 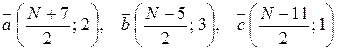 .
.
1. Найти координаты векторов 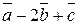 ;
; 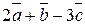 .
.
2. Проверить, что векторы 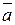 и
и 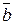 образуют базис на плоскости. Найти координаты вектора
образуют базис на плоскости. Найти координаты вектора 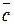 в этом базисе.
в этом базисе.
3. Определить при каком значении параметра 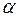 векторы
векторы 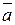 и
и 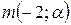 будут коллинеарными.
будут коллинеарными.
4. Найти координаты вектора 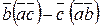 .
.
5. Вычислить 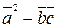 ,
, 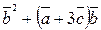 .
.
6. Найти косинус угла между векторами 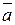 и
и 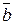 .
.
Задание 2
В пространстве относительно некоторого базиса даны координаты трех векторов:
при N – четном: 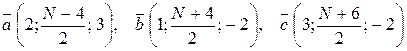 ;
;
при N – нечетном: 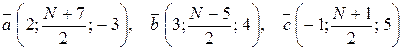 .
.
1. Найти координаты векторов 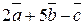 ,
, 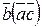 .
.
2. Вычислить 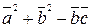 ;
; 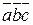 .
.
3. Найти косинус угла между векторами 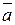 и
и 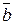 .
.
Задание 3
На плоскости относительно декартовой системы координат даны координаты трех точек:
при N – четном: 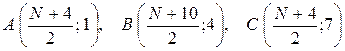 ;
;
при N – нечетном: 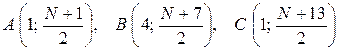 .
.
Найти:
1. Координаты вектора 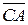 .
.
2. Координаты точек 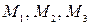 , делящих отрезки
, делящих отрезки 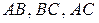 в отношениях
в отношениях 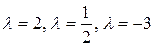 , соответственно.
, соответственно.
3. Координаты центра тяжести треугольника 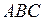 .
.
4. Длину отрезка 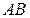 .
.
5. Площадь треугольника 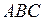 .
.
6. Угол 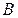 .
.
Задание 4
На плоскости относительно декартовой системы координат даны координаты вершин треугольника:
при N – четном: 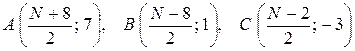 ;
;
при N – нечетном: 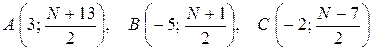 .
.
Найти:
1. Уравнения сторон треугольника.
2. Уравнение прямой BN, параллельной стороне AC.
3. Уравнение медианы CD.
4. Уравнение высоты AE.
5. Угол B.
6. Написать уравнение окружности с центром в A, для которой BC служит касательной.
Задание 5
Относительно декартовой системы координат даны координаты точки:
при N – четном: 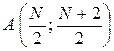 ;
;
при N – нечетном: 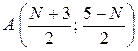 .
.
Найти:
1. Угловой коэффициент прямой 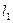 , проходящей через точку
, проходящей через точку 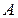 параллельно вектору
параллельно вектору 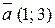 .
.
2. Уравнение прямой 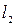 , проходящей через точку
, проходящей через точку 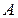 под углом
под углом 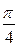 к прямой
к прямой 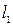 .
.
3. Уравнение прямой 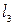 , проходящей через точку
, проходящей через точку 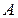 и отсекающей на осях координат равные отрезки.
и отсекающей на осях координат равные отрезки.
4. Косинус угла между прямыми 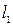 и
и 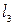 .
.
5. Уравнение прямой 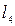 , проходящей через начало координат параллельно прямой
, проходящей через начало координат параллельно прямой 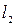 .
.
6. Расстояние между прямыми 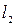 и
и 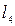 .
.
7. Координаты точки 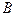 пересечения прямых
пересечения прямых 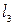 и
и 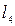 .
.
8. Расстояние от точки 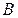 до прямой
до прямой 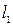 .
.
Задание 6
Определить, какие линии задаются уравнениями. Найти их геометрические характеристики. Построить линии.
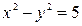 | 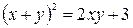 | 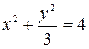 | |||
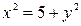 | 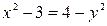 | 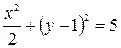 | |||
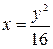 | 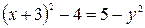 | 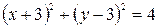 | |||
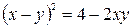 | 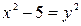 | 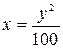 | |||
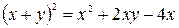 | 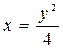 | 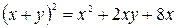 | |||
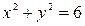 | 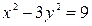 | 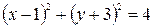 | |||
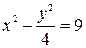 | 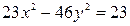 | 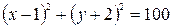 | |||
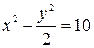 | 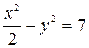 | 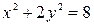 | |||
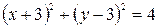 | 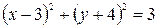 | 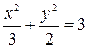 | |||
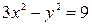 | 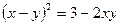 | 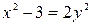 |
Задание 7
Составить каноническое уравнение эллипса и гиперболы, зная, что расстояние между фокусами равно 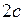 , большая полуось равна
, большая полуось равна 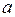 .
.
При N – четном: 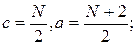
при N – нечетном: 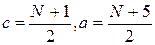 .
.
Найти:
1. Эксцентриситет эллипса; эксцентриситет гиперболы.
2. Уравнения директрис эллипса и гиперболы.
3. Расстояние от правого фокуса эллипса до ближайшей директрисы.
4. Длину отрезка асимптоты гиперболы, заключенного между её центром и директрисой.
5. Расстояния от фокусов гиперболы до её асимптот.
6. Уравнение сопряженной гиперболы; её эксцентриситет, уравнения директрис.
Задание 8
В данной системе координат парабола имеет каноническое уравнение. Составить это уравнение, зная, что расстояние от фокуса до директрисы равно 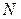 .
.
Найти:
1. Координаты фокуса.
2. Уравнение директрисы.
3. Координаты точек пересечения параболы с окружностью 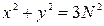 .
.
Задание 9
1. Составить уравнение и построить геометрическое место точек, находящихся к точке А(3, 0) вдвое ближе, чем к прямой х = 12.
2. Составить уравнение и построить линию, каждая точка которой отстоит от точки А (– 4, 0) втрое дальше, чем от начала координат.
3. Составить уравнение геометрического места точек, равноотстоящих от точек М(1, 5) и N(3, – 3).
4. Составить уравнение и построить линию, расстояния каждой точки которой от начала координат и от точки А(5, 0) относятся как 2 : 1.
5. Составить уравнение и построить линию, расстояние каждой точки которой от точки А (– 1, 0) вдвое меньше расстояния ее от прямой х = – 4.
6. Составить уравнение и построить линию, расстояние каждой точки которой от точки А (2, 0) и от прямой 5х + 8 = 0 относятся как 5 : 4.
7. Составить уравнение и построить линию, каждая точка которой находится вдвое дальше от точки А (4, 0), чем от точки B(1, 0).
8. Составить уравнение и построить линию, расстояние каждой точки которой от точки А (2, 0) и от прямой 2х + 5 = 0 относятся как 5 : 4.
9. Составить уравнение и построить линию, расстояние каждой точки которой от точки А (3, 0) вдвое меньше расстояния ее от точки B (26, 0).
10. Составить уравнение и построить линию, каждая точка которой одинаково удалена от точки А (0, 2) и от прямой y – 4 = 0.
11. Составить уравнение и построить линию, каждая точка которой равно отстоит от оси ординат и от окружности x2 + y2 = 4x.
12. Составить уравнение и построить линию, каждая точка которой равно удалена от точки А (2, 6) и от прямой y + 2 = 0.
13.Определить траекторию точки М, которая при своем движении всегда остается вдвое ближе к точке А (1, 0), чем к точке В (4, 0). Построить линию.
14. Составить уравнение геометрического места точек, одинаково удаленных от точки А (0, 1) и прямой y + 5 = 0.
15. Тело движется так, что в любой момент времени одинаково удалено от точки А (2, 0) и прямой x – 6 = 0. Найти уравнение траектории движения тела.
16. Тело движется так, что в любой момент времени находится ближе к точке А (4, 0), чем к точке В (–4, 0), на две единицы масштаба. Найти уравнение траектории движения тела.
17. Составить уравнение и построить линию, расстояние каждой точки которой от точки А (–2, 0) вдвое меньше расстояния ее от прямой х = 3.
18. Составить уравнение и построить линию, расстояние каждой точки которой от точки А (2, 1) и от прямой 4х + 6 = 0 относятся как 3 : 4.
19. Составить уравнение и построить линию, каждая точка которой втрое дальше от точки В (–2, 0), чем от точки А (4, 1).
20. Составить уравнение и построить линию, расстояния каждой точки которой от точки В(1, 0) и от прямой 2х + 5 = 0 относятся как 4 : 5.
21. Построить геометрическое место точек, расстояние от которых до точки А (2, 0) вдвое меньше расстояния до точки С(23, 0).
22. Составить уравнение и построить линию, каждая точка которой равноудалена от точки В (2, 0) и от прямой y – 2 = 0.
23. Составить уравнение и построить линию, каждая точка которой равноудалена от оси ординат и от окружности
(x – 1)2+y2=4.
24. Составить уравнение и построить линию, каждая точка которой равноудалена от точки С (1, 5) и от прямой y + 4 = 0.
25. Составить уравнение и построить геометрическое место точек, находящихся к точке В (2, 1) вдвое ближе, чем к прямой х = 7.
26. Составить уравнение окружности, которая имеет центр на пересечении прямых 4x – 3y + 10 = 0, 4x – 3y – 30 = 0 и равный 6 радиус.
27. Составить уравнение и построить линию, каждая точка которой отстоит от точки А (–3, 1) втрое дальше, чем от начала координат.
28. Составить уравнение геометрического места точек, равноудаленных от точек М (–1, 6) и N (4, –7).
29. Определить траекторию точки M (x, y), движущейся так, что разность квадратов расстояний от нее до биссектрис координатных углов остается равной 8.
30. Написать уравнение геометрического места точек, разность квадратов расстояний от которых до прямой 3x + 4y = 0 и до оси Ox остается постоянной и равной 2,4.
Типовой расчет № 2
Определители, их свойства. Алгебраические дополнения
И миноры. Формулы Крамера
Задание 1
Вычислить определители матриц 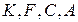 . Для матриц
. Для матриц 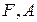 найти миноры
найти миноры 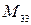 ,
, 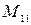 ,
, 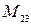 и алгебраические дополнения
и алгебраические дополнения 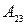 ,
, 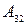 ,
, 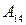 ,
, 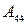 соответствующих элементов.
соответствующих элементов.
Провести вычисления непосредственно и с использованием MS Excel.
1–3 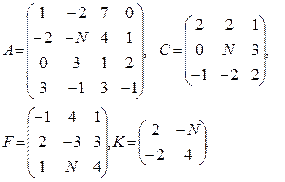 | 4–6 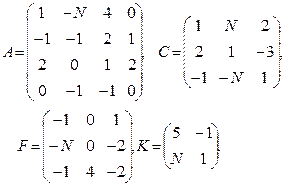 |
7–9 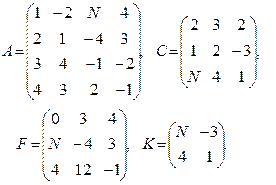 | 10–12 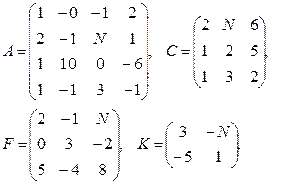 |
13–15 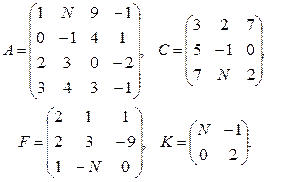 | 16–18 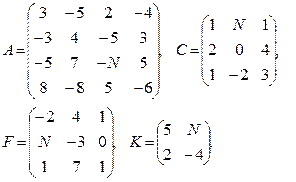 |
19–21 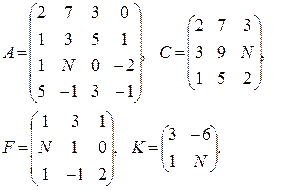 | 22–24 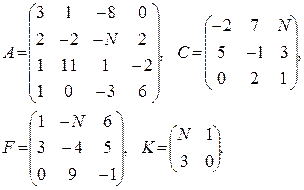 |
25–27 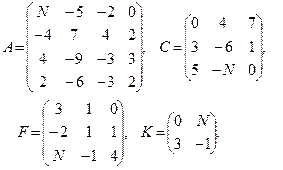 | 28–30 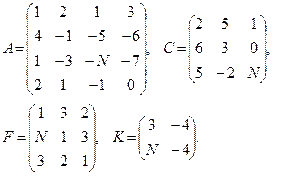 |
Задание 2
Найти неизвестное число x из следующих уравнений:
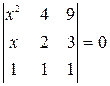 | 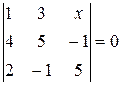 | 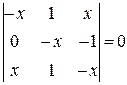 | 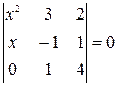 |
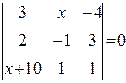 | 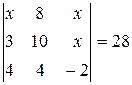 | 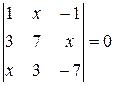 | 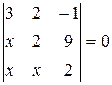 |
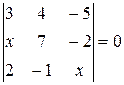 | 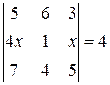 | 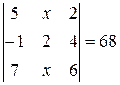 | 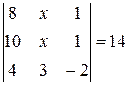 |
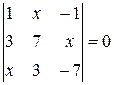 | 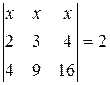 | 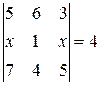 | 16 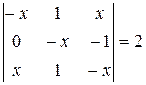 |
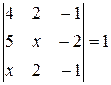 | 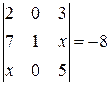 | 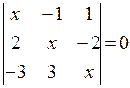 | 20 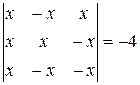 |
21 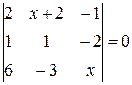 | 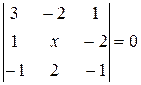 | 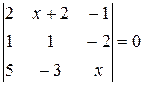 | 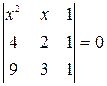 |
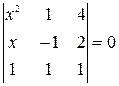 | 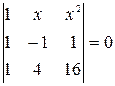 | 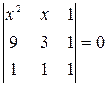 | 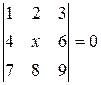 |
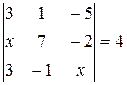 | 30 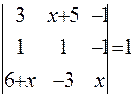 |
Задание 3
Вычислить определитель матрицы А двумя способами: 1) по-лучением нулей в 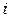 -й строке и разложением по элементам этой строки; 2) получением нулей в
-й строке и разложением по элементам этой строки; 2) получением нулей в 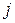 -м столбце и разложением по элементам этого столбца.
-м столбце и разложением по элементам этого столбца.
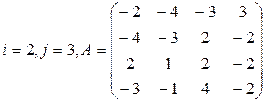 | 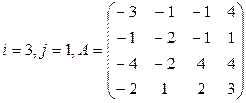 |
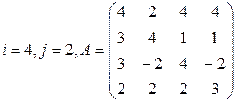 | 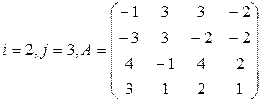 |
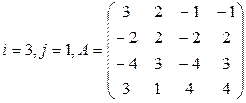 | 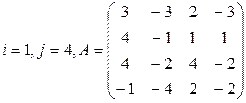 |
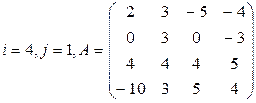 | 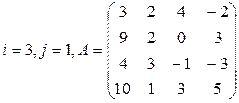 |
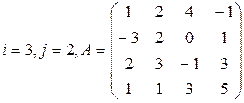 | 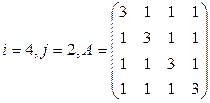 |
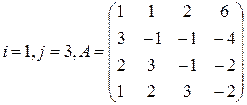 | 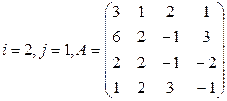 |
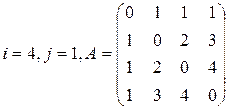 | 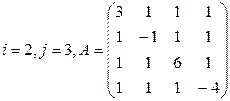 |
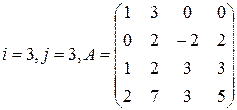 | 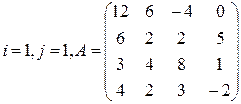 |
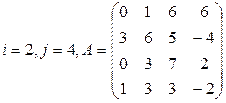 | 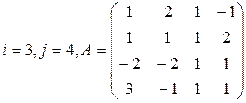 |
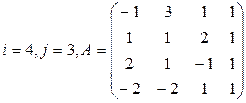 | 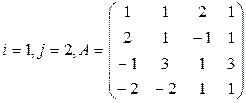 |
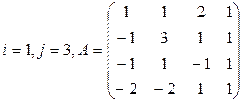 | 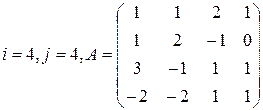 |
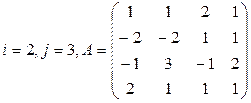 | 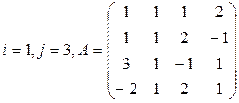 |
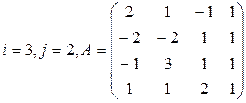 | 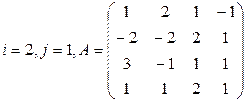 |
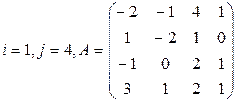 | 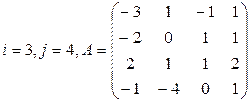 |
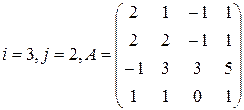 | 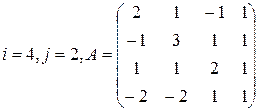 |
Задание 4
Вычислить определитель четвертого порядка, используя как алгебраические дополнения, так и элементарные преобразования матриц.
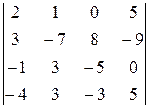 | 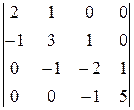 | 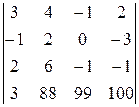 | ||
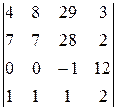 | 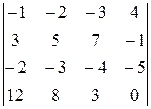 | 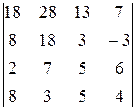 | ||
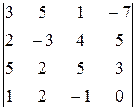 | 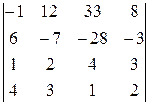 | 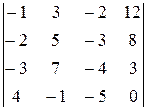 | ||
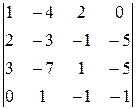 | 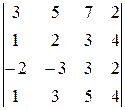 | 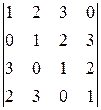 | ||
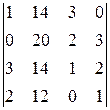 | 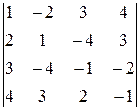 | 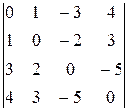 | ||
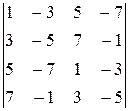 | 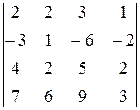 | 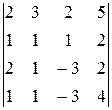 | ||
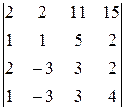 | 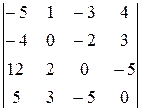 | 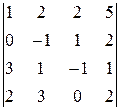 | ||
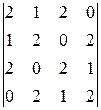 | 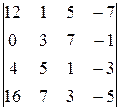 | 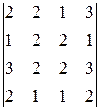 | ||
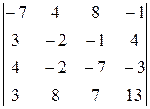 | 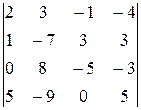 | 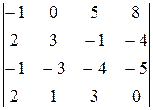 | ||
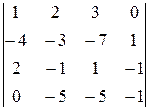 | 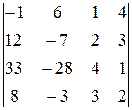 | 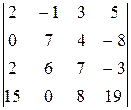 | ||
Задание 5
Варианты 1–15
С первого склада каждому из трех получателей отправлено по 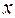 единиц груза, со второго склада – по
единиц груза, со второго склада – по 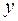 единиц, с третьего – по
единиц, с третьего – по 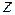 единиц груза.
единиц груза. 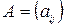 – матрица транспортных расходов (
– матрица транспортных расходов ( 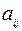 – затраты на перевозку единицы груза с
– затраты на перевозку единицы груза с 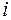 - го склада
- го склада 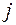 - му получателю). Определить
- му получателю). Определить 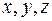 если первый получатель затратил на перевозку
если первый получатель затратил на перевозку 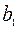 , второй –
, второй – 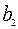 , третий –
, третий – 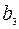 денежных единиц. Найти решение системы методом Крамера.
денежных единиц. Найти решение системы методом Крамера.
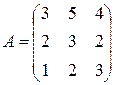 , , 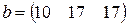 | 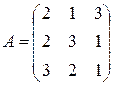 , , 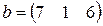 |
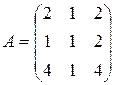 , , 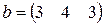 | 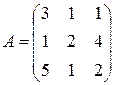 , , 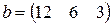 |
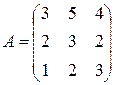 , , 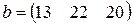 | 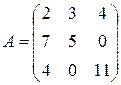 , , 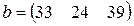 |
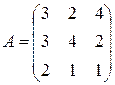 , , 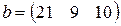 | 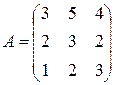 , , 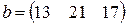 |
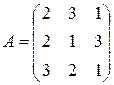 , , 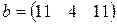 | 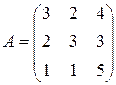 , , 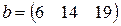 |
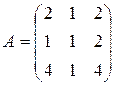 , , 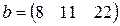 | 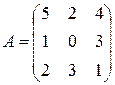 , , 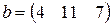 |
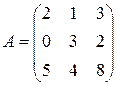 , , 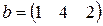 | 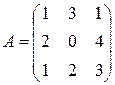 , , 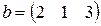 |
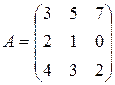 , , 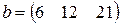 |
Варианты 16–30
Матрица 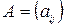 , где
, где 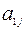 – цена единицы товара
– цена единицы товара 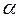 в
в 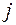 -ом магазине,
-ом магазине, 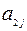 – цена единицы товара
– цена единицы товара 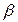 в
в 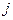 -м магазине,
-м магазине, 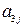 – цена единицы товара
– цена единицы товара 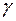 в
в 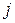 -м магазине. Один и тот же набор товаров стоит в
-м магазине. Один и тот же набор товаров стоит в 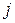 -м магазине. Сколько единиц товаров входит в набор? Найти решение системы методом Крамера.
-м магазине. Сколько единиц товаров входит в набор? Найти решение системы методом Крамера.
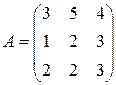 , , 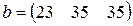 | 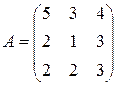 , , 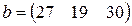 |
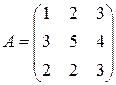 , , 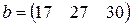 | 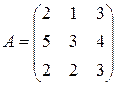 , , 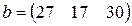 |
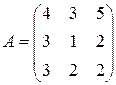 , , 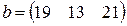 | 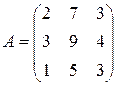 , , 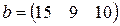 |
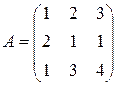 , , 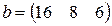 | 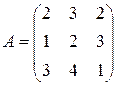 , , 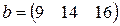 |
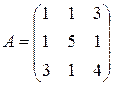 , , 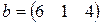 | 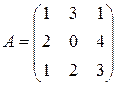 , , 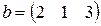 |
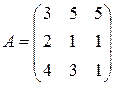 , , 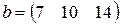 | 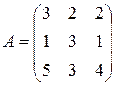 , , 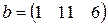 |
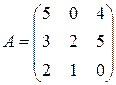 , , 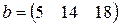 | 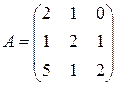 , , 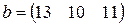 |
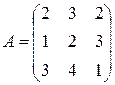 , , 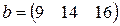 |
Задание 6
Решить системы уравнений с помощью теоремы Крамера. Провести вычисления непосредственно и с использованием MS Excel.
1–3 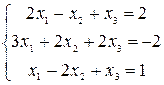 | 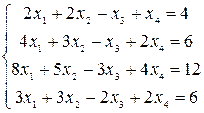 |
4–6 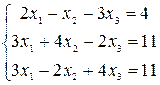 | 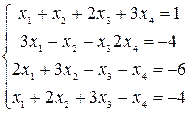 |
7–9 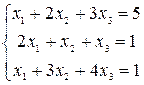 | 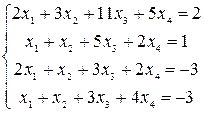 |
10–12 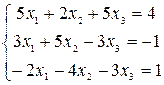 | 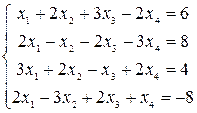 |
13–15 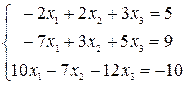 | 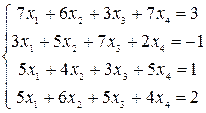 |
16–18 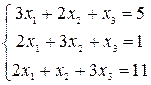 | 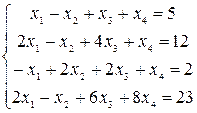 |
19–21 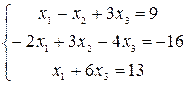 | 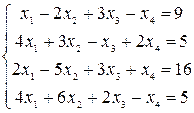 |
22–24 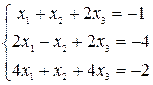 | 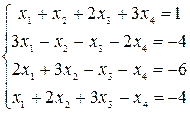 |
25–27 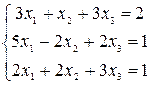 | 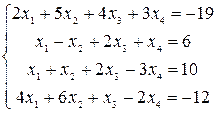 |
28–30 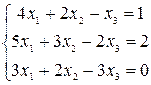 | 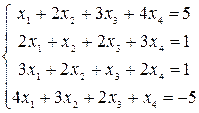 |
Типовой расчет № 3
Операции над матрицами
Задание 1
Варианты 1–7
Предприятие производит продукцию трех видов и использует сырье двух типов. Нормы затрат сырья на единицу продукции каждого вида заданы матрицей А. Стоимость единицы сырья каждого типа задана матрицей В. Каковы общие затраты предприятия на производство С единиц продукции каждого вида?
А= 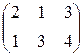 , В= , В= 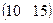 , , 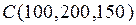 | А= 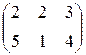 , В= , В= 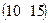 , , 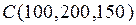 | А= 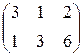 , В= , В= 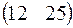 , , 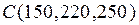 | А= 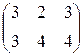 , В= , В= 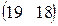 , , 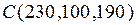 |
А= 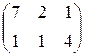 , В= , В= 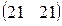 , , 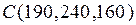 | А= 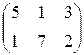 , В= , В= 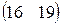 , , 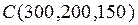 | А= 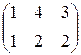 , В= , В= 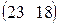 , , 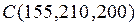 |
Варианты 8–15
Определить затраты фирмы, производящей 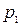 единиц продукции П1,
единиц продукции П1, 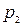 – продукции П2 и
– продукции П2 и 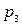 – продукции П3, если нормы затрат сырья на производство единицы продукции каждого вида заданы матрицей А. Стоимость единицы сырья каждого типа задана матрицей В.
– продукции П3, если нормы затрат сырья на производство единицы продукции каждого вида заданы матрицей А. Стоимость единицы сырья каждого типа задана матрицей В.
П=(80,90,130), А= 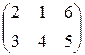 , В= , В= 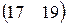 . . | П=(85,80,130), А= 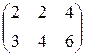 , В= , В= 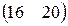 . . |
П=(70,90,230), А= 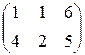 , В== , В== 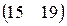 . . | П=(80,60,100), А= 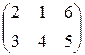 , В== , В== 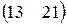 . . |
П=(65,100,50), А= 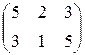 , В== , В== 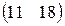 . . | П=(80,90,160), А= 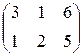 , В== , В== 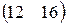 . . |
П=(40,80,120), А= 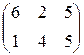 , В== , В== 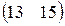 . . | П=(30,90,140), А= 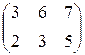 , В== , В== 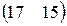 . . |
Варианты 16–22
Прибыль, полученная от затрат сырья на единицу продукции каждого вида некоторой фирмы, задана матрицей А, доход от единицы сырья каждого типа задан матрицей В. Определить прибыль фирмы, производящей изделия двух видов и использующей сырье двух типов, если фирма собирается производить С изделий первого вида и D – второго.
А= 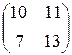 , В= , В= 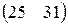 , С=300, D=250. , С=300, D=250. | А= 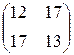 , В= , В= 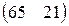 , С=400, D=270. , С=400, D=270. |
А= 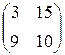 , В= , В= 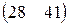 , С=350, D=260. , С=350, D=260. | А= 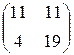 , В= , В= 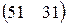 , С=250, D=280. , С=250, D=280. |
А= 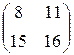 , В= , В= 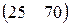 , С=300, D=290. , С=300, D=290. | А= 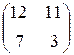 , В= , В= 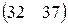 , С=600, D=210. , С=600, D=210. |
А= 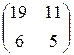 , В= , В= 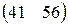 , С=160, D=230. , С=160, D=230. |
Варианты 23–30
Предприятие производит продукцию двух видов и использует сырье двух типов. Нормы затрат сырья на единицу продукции каждого вида заданы матрицей А. Стоимость единицы сырья каждого типа задана матрицей В. Каковы общие затраты предприятия на производство C единиц продукции первого вида и D единиц второго вида?
А= 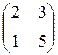 , В= , В= 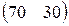 , С=100, D=150. , С=100, D=150. | А= 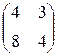 , В= , В= 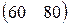 , С=200, D=160. , С=200, D=160. |
А= 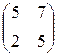 , В= , В= 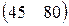 , С=500, D=170. , С=500, D=170. | А= 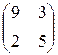 , В= , В= 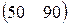 , С=300, D=190. , С=300, D=190. |
А= 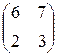 , В= , В= 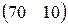 , С=400, D=120. , С=400, D=120. | А= 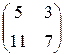 , В= , В= 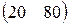 , С=600, D=130. , С=600, D=130. |
А= 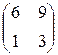 , В= , В= 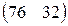 , С=150, D=170. , С=150, D=170. | А= 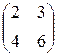 , В= , В= 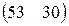 , С=280, D=110. , С=280, D=110. |
Задание 2
Варианты 1–15
Три цеха выпускают продукцию 5 видов. Матрица плана А размерности 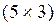 (
( 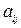 – запланированное количество продукции
– запланированное количество продукции 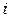 -го вида для
-го вида для 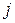 -го цеха). В – матрица размерности
-го цеха). В – матрица размерности 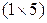 – матрица цен продукции (
– матрица цен продукции ( 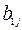 – цена единицы количества продукции
– цена единицы количества продукции 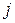 -го вида). 1) Найти матрицу
-го вида). 1) Найти матрицу 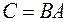 . Какой смысл имеют элементы этой матрицы? 2) Найти сумму элементов
. Какой смысл имеют элементы этой матрицы? 2) Найти сумму элементов 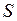 этой матрицы и указать её смысл. 3) Найти матрицу
этой матрицы и указать её смысл. 3) Найти матрицу 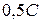 и указать смысл её элементов.
и указать смысл её элементов.
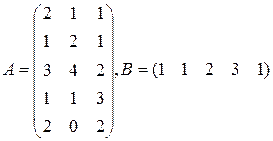 | 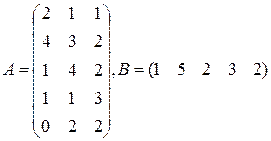 |
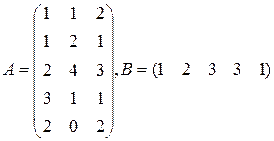 | 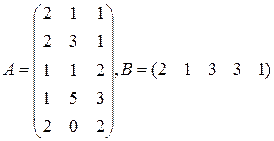 |
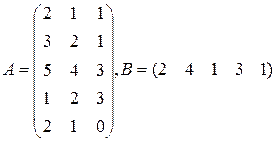 | 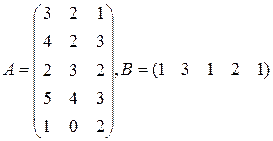 |
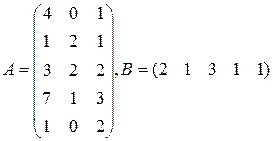 | 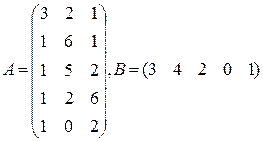 |
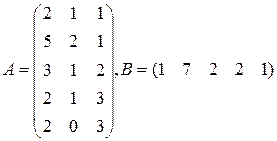 | 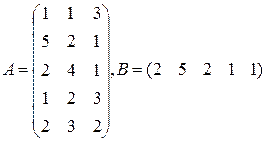 |
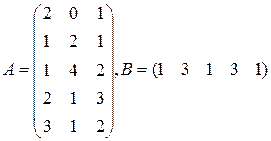 | 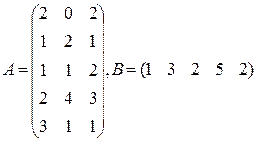 |
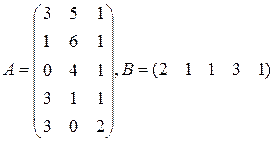 | 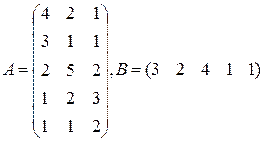 |
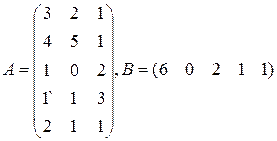 |
Варианты 16–30
Цех выпускает три вида изделий, при приготовлении любого изделия производят 5 операций. Матрица А размерности 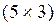 – матрица затрат рабочего времени (
– матрица затрат рабочего времени ( 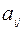 – время
– время 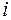 -й операции при изготовлении изделия
-й операции при изготовлении изделия 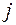 -го вида). В – матрица размерности
-го вида). В – матрица размерности 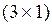 – матрица плана выпуска (
– матрица плана выпуска ( 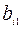 – число изделий
– число изделий 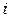 - го вида намеченных к выпуску). 1) Найти матрицу
- го вида намеченных к выпуску). 1) Найти матрицу 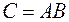 . Какой смысл имеют элементы этой матрицы? 2) Найти сумму элементов
. Какой смысл имеют элементы этой матрицы? 2) Найти сумму элементов 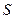 этой матрицы и указать её смысл. 3) Найти матрицу
этой матрицы и указать её смысл. 3) Найти матрицу 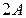 и указать смысл её элементов.
и указать смысл её элементов.
16 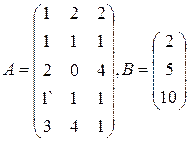 | 17 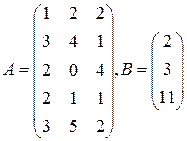 | 18 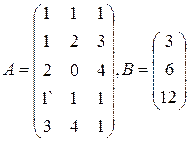 |
19 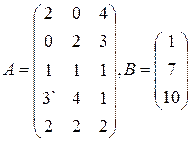 | 20 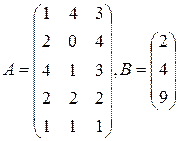 | 21 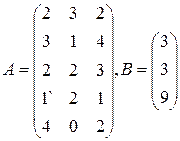 |
22 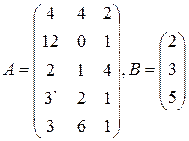 | 23 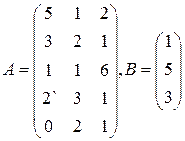 | 24 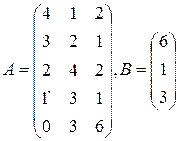 |
25 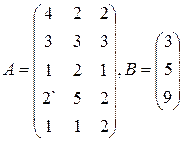 | 26 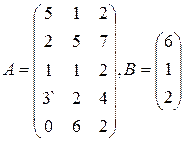 | 27 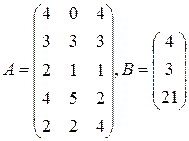 |
28 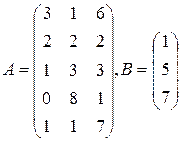 | 29 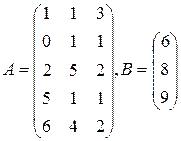 | 30 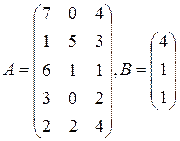 |
Задание 3
Даны матрицы A, B, C, D, E, F, G.
1. Найти следующие комбинации этих матриц:
а) 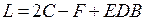 ; б)
; б) 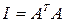 , в)
, в) 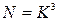 .
.
2. Проверить равенство 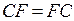 .
.
3. Найти значение заданного многочлена 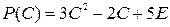 от заданной матрицы С (всюдув задании E – единичная матрица нужного размера)
от заданной матрицы С (всюдув задании E – единичная матрица нужного размера)
1–3 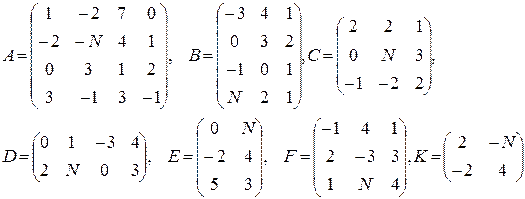 |
4–6 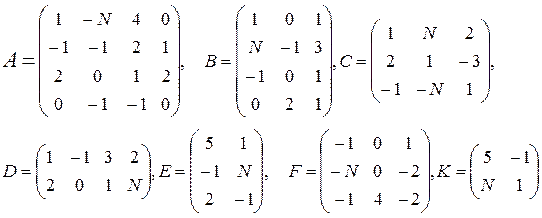 |
7–9 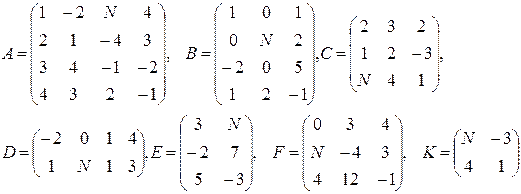 |
10–12 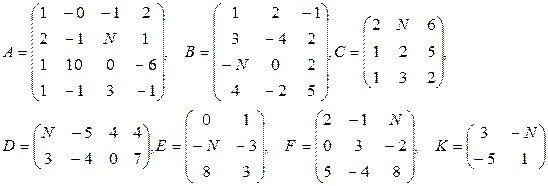 |
13–15 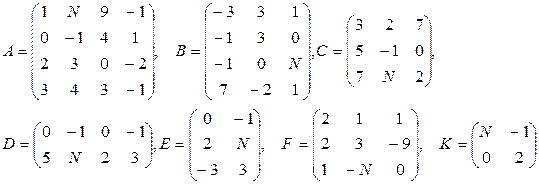 |
16–18 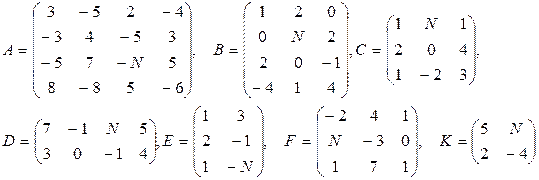 |
19–21 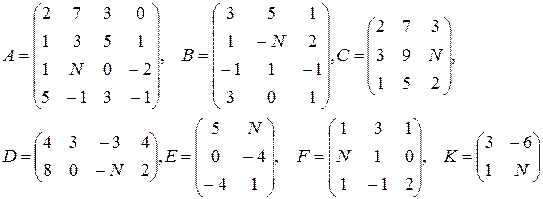 |
22–24 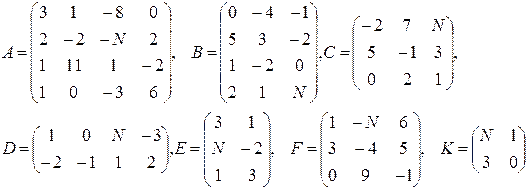 |
25–27 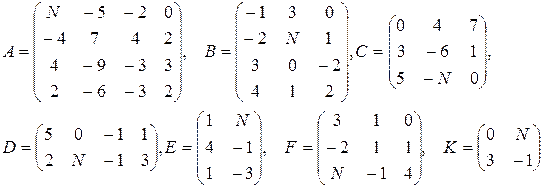 |
28–30 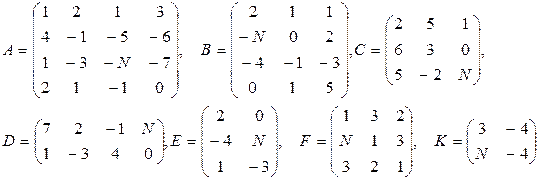 |
Задание 4
Решить следующие матричные уравнения:
1–3 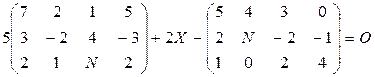 | |
4–6 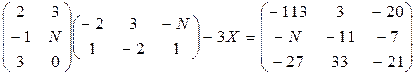 | |
7–9 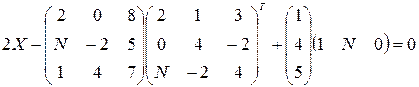 | |
10–12 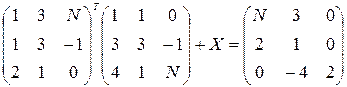 | |
13–15 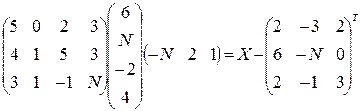 | |
16–18 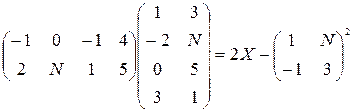 | |
19–21 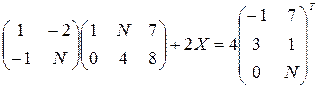 | |
22–24 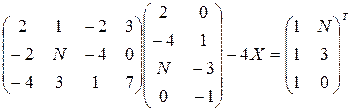 | |
25–27 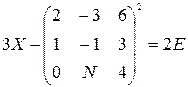 | 28–30 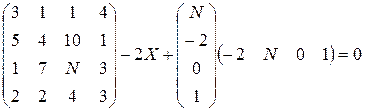 |
Задание 5
Найти матрицы, обратные к данным методом алгебраических дополнений и методом Гаусса, сделать проверку.
