Простейшие свойства колец.

Пусть (K,+, ·) — кольцо. Так как (K, +) — абелева группа, учитывая свойства групп получим

СВ-ВО 1 . Во всяком кольце (K,+, ·) имеется единственный нулевой элемент 0 и для всякого a ∈ K имеется единственный противоположный ему элемент −a.

СВ-ВО 2. ∀ a, b, c ∈ K (a + b = a + c ⇒ b = c).

СВ-ВО 3. Для любых a, b ∈ K в кольце K существует единственная разность a − b, причем a − b = a + (−b). Таким образом, в кольце K определена операция вычитания, при этом она обладает свойствами 1′—8′.

СВ-ВО 4 . Операция умножения в K дистрибутивна относительно операции вычитания, т.е. ∀ a, b, c ∈ K ((a − b)c = ac − bc ∧ c(a − b) = ca − cb).

Док-во. Пусть a, b, c ∈ K. Учитывая дистрибутивность операции · в K относительно операции + и определение разности элементов кольца, получим (a − b)c + bc = ((a − b) + b)c = ac, откуда по определению разности следует, что (a − b)c = ac − bc.

Аналогично доказывается правый закон дистрибутивности операции умножения относительно операции вычитания.

СВ-В 5. ∀ a ∈ K a0 = 0a = 0.

Доказательство. Пусть a ∈ K и b—произвольный элемент из K. Тогда b − b = 0 и поэтому, учитывая предыдущее свойство, получим a0 = a(b − b) = ab − ab = 0.

Аналогично доказывается, что 0a = 0.

СВ-ВО 6. ∀ a, b ∈ K (−a)b = a(−b) = −(ab).

Доказательство. Пусть a, b ∈ K. Тогда (−a)b + ab = ((−a) + a)b =

= 0b = 0. Значит, (−a)b = −(ab).

Аналогично доказывается равенство a(−b) = −(ab).

СВ-ВО 7. ∀ a, b ∈ K (−a)(−b) = ab.

Доказательство. В самом деле, применяя дважды предыдущее свойство, получим (−a)(−b) = −(a(−b)) = −(−(ab)) = ab.

ЗАМЕЧАНИЕ. Свойства 6 и 7 называют правилами знаков в кольце.

Из дистрибутивности операции умножения в кольце K относительно операции сложения и свойств 6 и 7 вытекает следующее

СВ-ВО 8. Пусть k, l—произвольные целые числа. Тогда ∀ a, b ∈ K (ka)(lb) = (kl)ab.

Подкольцо

Подкольцом кольца (K,+, ·) называется подмножество H множества K, которое замкнуто относительно операций + и ·, определенных в K, и само является кольцом относительно этих операций.

Примеры подколец:

Так, Z —подкольцо кольца (Q,+, ·), Q—подкольцо кольца (R,+, ·), Rn×n —подкольцо кольца (Cn×n,+, ·), Z[x]—подкольцо кольца (R[x],+, ·), D[a,b] —подкольцо кольца (C[a,b],+, ·).

Во всяком кольце (K,+, ·) само множество K, а также одноэлементное подмножество {0} являются подкольцами кольца (K,+, ·). Это так называемые тривиальные подкольца кольца (K,+, ·).

Простейшие свойства подколец.

Пусть H — подкольцо кольца (K,+, ·), т.е. (H,+, ·) само является кольцом. Значит, (H, +)—группа, т.е. H —подгруппа группы (K, +). Поэтому справедливы следующие утверждения.

СВ-ВО 1. Нулевой элемент подкольца H кольца K совпадает с нулевым элементом кольца K.

СВ-ВО 2 . Для всякого элемента a подкольца H кольца K противоположный ему элемент в H совпадает с −a, т.е. с противоположным ему элементом в K.

СВ-ВО 3. Для любых элементов a и b подкольца H их разность в H совпадает с элементом a − b, т.е. с разностью этих элементов в K.

Признаки подкольца.

ТЕОРЕМА 1 (первый признак подкольца).

Непустое подмножество H кольца K с операциями + и · является подкольцом кольцаK тогда итолькотогда, когда оно удовлетворяет следующим условиям:

∀ a, b ∈ H a + b ∈ H, (1)

∀ a ∈ H − a ∈ H, (2)

∀ a, b ∈ H ab ∈ H. (3)

Док-во.

Необходимость. Пусть H — подкольцо кольца (K,+, ·). Тогда H —подгруппа группы (K, +). Поэтому по первому признаку подгруппы (в аддитивной формулировке), H удовлетворяет условиям (1) и (2). Кроме того, H замкнуто относительно операции умножения, определенной в K, т.е. H

удовлетворяет и условию (3).

Достаточность. Пусть H ⊂ K, H 6= ∅ и H удовлетворяет условиям ( 1) − ( 3). Из условий (1) и (2) по первому признаку подгруппы следует, что H —подгруппа группы (K, +), т.е. (H, +)—группа. При этом, так как (K, +)—абелева группа, (H, +) также абелева. Кроме того, из условия (3) следует, что умножение является бинарной операцией на множестве H. Ассоциативность операции · в H и ее дистрибутивность относительно операции + следуют из того, что такими свойствами обладают операции + и · в K.

ТЕОРЕМА 2 (второй признак подкольца).

Непустое подмножество H кольца K с операциями + и · является

подкольцом кольца K т. и т. т, когда оно удовлетворяет следующим условиям:

∀ a, b ∈ H a − b ∈ H, (4)

∀ a, b ∈ H ab ∈ H. (5)

Доказательство этой теоремы аналогично доказательству теоремы 1.

При этом используется теорема 2′ (второй признак подгруппы в аддитивной формулировке) и замечание к ней.

7.Поле (определение, виды, свойства, признаки).

Полем называется коммутативное кольцо с единицей e не равно 0, в котором всякий элемент, отличный отнуля имеет обратный.

Классическими примерами числовых полей являются поля (Q,+, ·), (R,+, ·), (C,+, ·).

СВОЙСТВО 1. Во всяком поле F справедлив закон сокращения

на общий множитель, отличный от нуля, т.е.

∀ a, b, c ∈ F (ab = ac ∧ a не равно 0 ⇒ b = c).

СВОЙСТВО 2. Во всяком поле F нет делителей нуля.

СВОЙСТВО 3. Кольцо (K,+, ·) является полем тогда и только

тогда, когда множество K \ {0} есть коммутативная группа относительно операции умножения.

СВОЙСТВО 4 . Конечное ненулевое коммутативное кольцо(K,+, ·) без делителей нуля является полем.

Частное элементов поля.

Пусть (F,+, ·)—поле.

Частным элементов a и b поля F, где b не равно 0,

называется такой элемент c ∈ F, что a = bc.

СВОЙСТВО 1. Для любых элементов a и b поля F, где b не равно 0, существует единственное частное a/b, причем a/b= ab−1.

СВОЙСТВО 2. ∀ a ∈ F \ {0}

a/a= e и ∀ a ∈ F a/e= a.

СВОЙСТВО 3. ∀ a, c ∈ F ∀ b, d ∈ F \ {0}

a/b=c/d ⇔ ad = bc.

СВОЙСТВО 4. ∀ a, c ∈ F ∀ b, d ∈ F \ {0}

a/b*c/d=ac/bd

СВОЙСТВО 5. ∀ a ∈ F ∀ b, c, d ∈ F \ {0}

(a/b)/(c/d)=ad/bc

СВОЙСТВО 6. ∀ a ∈ F ∀ b, c ∈ F \ {0}

ac/bc=a/b

СВОЙСТВО 7. ∀ a ∈ F ∀ b, c ∈ F \ {0}

(a/b)/c=a/bc

СВОЙСТВО 8. ∀ a, b ∈ F ∀ c ∈ F \ {0}

ab/c=ab/c

Поле F, единица которого имеет конечный порядок p в группе (F, +), называется полем характеристики p.

Поле F единица, которого имеет бесконечный порядок в группе (F, +), называется полем характеристики 0.

8. Подполе (определение, виды, свойства, признаки)

Подполем поля (F,+, ·) называется подмножество S множества F, которое замкнуто относительно операций+ и ·, определенных в F, и само является полем относительно этих операций.

Приведем некоторые примеры подполей Q—подполе поля (R,+, ·);

R—подполе поля (C,+, ·);

справедливы следующие утверждения.

СВОЙСТВО 1. Нулевой элемент подполя S поля F совпадает с

нулевым элементом поля F.

СВОЙСТВО 2 . Для всякого элемента a подполя S поля F противоположный ему элемент в S совпадает с −a, т.е. с противоположным ему элементом в F.

СВОЙСТВО 3. Для любых элементов a и b подполя S поля F их

разность в S совпадает с a−b т.е. с разностью этих элементов в F.

СВОЙСТВО 4. Единица подполя S поля F совпадает с единицей

e поля F.

СВОЙСТВО 5 . Для всякого элемента a подполя S поля F, от-

личного от нуля, обратный к нему элемент в S совпадает с a−1, т.е. с элементом, обратным к a в F.

Признаки подполя.

ТЕОРЕМА 1 (первый признак подполя).

Подмножество H поля F c операциями +, ·, содержащее ненулевой

элемент, является подполем поля (F,+, ·) тогда и только тогда, когда оно удовлетворяет следующим условиям:

∀ a, b ∈ H a + b ∈ H, (1)

∀ a ∈ H − a ∈ H, (2)

∀ a, b ∈ H ab ∈ H, (3)

∀ a ∈ H \ {0} a−1 ∈ H. (4)

ТЕОРЕМА2 (второй признак подполя).

Подмножество H поля F c операциями +, ·, содержащее ненулевой

элемент, является подполем поля (F,+, ·) тогда и только тогда, когда оно удовлетворяет следующим условиям:

∀ a, b ∈ H a − b ∈ H, (5)

∀ a ∈ H ∀ b ∈ H\{0} a/b ∈ H. (6)

10. Отношение делимости в кольце Z

Утверждение: для любых элементов a,b,c коммутативного кольца на множестве R, справедливы следующие импликации :

1) а|b, b|c => a|c

2) a|b, a|c => a| (b c)

3) a|b => a|bc

для любого a, b Z справедливо:

1) a|b ó ≠ b

2) a|b, b≠0 => |a|≤|b|

3)a|b и b|a ó |a|=|b|

Разделить с остатком целое число а на целое число b , значит найти такие целые числа q и r, что можно представить a=b*q + r, 0≤r≥|b|, где q – неполное частное , r- остаток

Теорема : Если a и b Z , b≠0, то а можно разделить на b с остатком ,причем неполное частное и остаток определяются однозначно .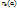

Следствие ,если a и b Z , b≠0, то b|a ó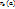

11. НОД и НОК

Наибольший общий делитель(НОД) чисел 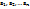Z называется некоторое число d, удовлетворяющее следующим условиям

1) d является общим делителем 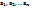т.е. d| , d| …d|

2) d делится на любой общий делитель чисел 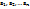т.е. d| , d| …d| => d| , d| …d|

Утверждение : если 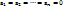,то для чисел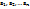

существует единственный НОД=0 ,если целые числа 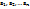не все равны нулю ,то для них существует хотя бы один НОД и они имеют ровно два НОД, которые отличаются только знаками.

Теорема : для любого натурального числа n≥2 и любых целых чисел 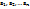существует НОД ,причем единственный такой что ( =((( ) )…, )

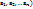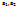Наименьшим общим кратным (НОК) целых чисел 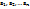называется любое целое число К , удовлетворяющее

1. , …

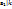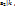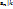
2. K делит любое общее кратное чисел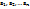

3. …

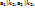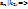
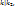
Утверждение : если n≥2 и хотя бы одно из целых чисел 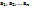равно нулю, то для них существует единственное НОК=0, если целые числа 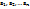≠0 для них существует хотя бы одно НОК ,и они имеют ровно два НОК ,которые отличаются только знаком.

Для целых чисел a и b выполняется следующее [a,b]=|a*b|/(a,b)

Теорема : для любых n≥2 и любых чисел 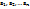существует единственное неотрицательное НОК , которое находится по формуле

[ ]=[…[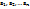