Простейшие свойства интегралов
Первообразная и неопределенный интеграл.
Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство 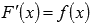 для любого х из заданного промежутка.
для любого х из заданного промежутка.
Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство 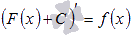 . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается 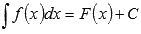 .
.
Выражение 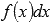 называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
Табличные интегралы
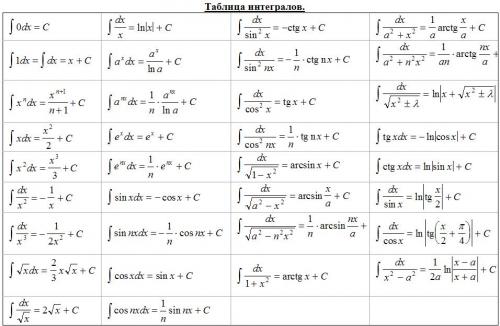
Простейшие свойства интегралов
1. Производная результата интегрирования равна подынтегральной функции.
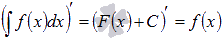
2. Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.
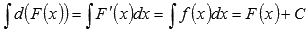
3. Коэффициент можно выносить за знак неопределенного интеграла.
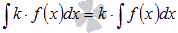
4. Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.
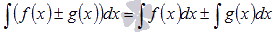
Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.
Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств:
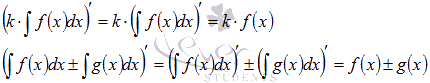
Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.
Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:
первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.
1.4.Инвариантность форм интегрирования.
Инвариантное интегрирование - вид интегрирования для функций, аргументом которых являются элементы группы или точки однородного пространства (любую точку такого пространства можно перевести в другую заданным действием группы).
функции f(x )сводится к вычислению интеграла от дифференциальной формы f.w, где
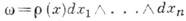 явная ф-ла для r( х )приводится ниже. Условие согласования имеет вид
явная ф-ла для r( х )приводится ниже. Условие согласования имеет вид 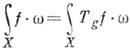 .
.
здесь Tg означает оператор сдвига на X с помощью gОG: Tgf(x)=f(g-1x). Пусть X=G - топология, группа, действующая на себе левыми сдвигами. И. и. существует тогда и только тогда, когда G локально компактна (в частности, на бесконечномерных группах И. и. не существует). Для подмножества 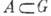 И. и. характеристических функции cA (равной 1 на A и 0 вне А)задаёт левую меру Xаара m(A). Определяющим свойством этой меры является её инвариантность при левых сдвигах: m(g-1A)=m(А)для всех gОG. Левая мера Хаара на группе определена однозначно с точностью до положит, скалярного множителя. Если известна мера Хаара m, то И. и. функции f даётся формулой
И. и. характеристических функции cA (равной 1 на A и 0 вне А)задаёт левую меру Xаара m(A). Определяющим свойством этой меры является её инвариантность при левых сдвигах: m(g-1A)=m(А)для всех gОG. Левая мера Хаара на группе определена однозначно с точностью до положит, скалярного множителя. Если известна мера Хаара m, то И. и. функции f даётся формулой 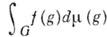 . Аналогичными свойствами обладает правая мера Хаара. Существует непрерывный гомоморфизм (отображение, сохраняющее групповое свойство) DG группы G в группу (относительно умножения) положит. чисел, для которого
. Аналогичными свойствами обладает правая мера Хаара. Существует непрерывный гомоморфизм (отображение, сохраняющее групповое свойство) DG группы G в группу (относительно умножения) положит. чисел, для которого 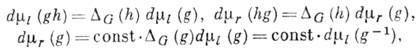
где dmr и dmi - правая и левая меры Хаара. Функцию DG(g) наз. модулем группы G. Если 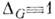 , то группа G наз. унимодулярной; в этом случае правая и левая меры Хаара совпадают. Компактные, полупростые и нильпотентные (в частности, коммутативные) группы унимодулярны. Если G - n-мерная группа Ли и q1, ...,qn - базис в пространстве левоинвариантных 1-форм на G, то левая мера Хаара на G задаётся n-формой
, то группа G наз. унимодулярной; в этом случае правая и левая меры Хаара совпадают. Компактные, полупростые и нильпотентные (в частности, коммутативные) группы унимодулярны. Если G - n-мерная группа Ли и q1, ...,qn - базис в пространстве левоинвариантных 1-форм на G, то левая мера Хаара на G задаётся n-формой 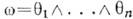 . В локальных координатах для вычисления
. В локальных координатах для вычисления 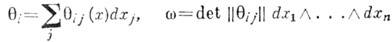
форм qi можно воспользоваться любой матричной реализацией группы G: матричная 1-форма g-1dg левоинвариантна, а её коэф. являются левоинвариантными скалярными 1-формами, из которых и выбирается искомый базис. Напр., полная матричная группа GL(n, R)унимодулярна и мера Хаара на ней задаётся формой. Пусть 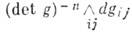 X=G/H - однородное пространство, для которого локально компактная группа G является группой преобразований, а замкнутая подгруппа Н - стабилизатором некоторой точки. Для того чтобы на X существовало И. и., необходимо и достаточно, чтобы для всех hОH выполнялось равенство DG(h)=DH(h). В частности, это верно в случае, когда Н компактна или полупроста. Полной теории И. и. на бесконечномерных многообразиях не существует.
X=G/H - однородное пространство, для которого локально компактная группа G является группой преобразований, а замкнутая подгруппа Н - стабилизатором некоторой точки. Для того чтобы на X существовало И. и., необходимо и достаточно, чтобы для всех hОH выполнялось равенство DG(h)=DH(h). В частности, это верно в случае, когда Н компактна или полупроста. Полной теории И. и. на бесконечномерных многообразиях не существует.
Замена переменных.

