Простейшие свойства определенного интеграла

1) Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых функций:

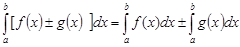
2) Постоянный множитель можно выносить за знак определенного интеграла

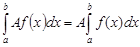
3) При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:

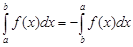
4) Определенный интеграл с одинаковыми пределами равен нулю: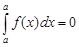

5) Отрезок интегрирования можно разделить на части:

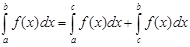
с-точка, лежащая между а и b.

6) Если 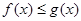на отрезке 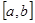, то .

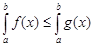Для вычисления определенного интеграла от функции 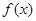, в том случае , когда можно найти соответствующую первообразную 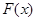, служит формула Ньютона-Лейбница:

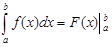=F(b)-F(a)

Рассмотрим нахождение простейших определенных интегралов.

Пример 1: Вычислить определенный интеграл .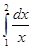

Решение: =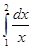

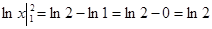
Пример 2:Вычислить определенный интеграл: .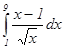

Решение: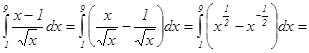

.

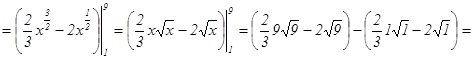
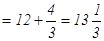Вычисление определенного интеграла

Методом замены переменной

При вычислении определенного интеграла методом замены переменной (способом подстановки) определенный интеграл 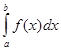преобразуется с помощью подстановк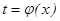и или 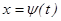в определенный интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются соответственно новыми пределами t₁ и t₂, которые находятся из исходной подстановки.

Из первой подстановки новые пределы интегрирования вычисляются непосредственно: .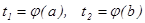

Из второй подстановки новые пределы интегрирования находятся путем решения уравнений .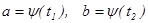

Таким образом, имеем

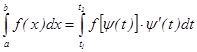
Пример 1: Вычислить определенный интеграл методом замены переменной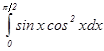

Решение: =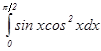

.

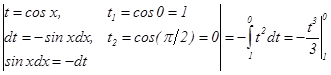
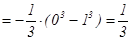Пример 2: Вычислить определенный интеграл: .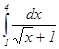

Решение: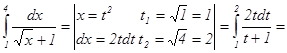

.

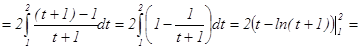
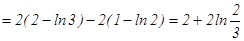Вычисление площадей плоских фигур.

у

+ +

0 a - bx

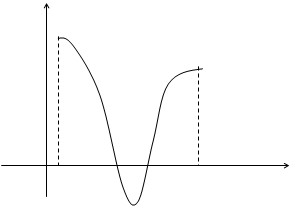
Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.

Для нахождения суммарной площади используется формула .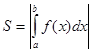

Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.

Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x², x = 2.

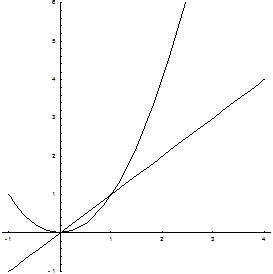
Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:

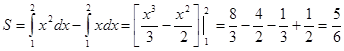(ед²)

Пример.

Вычислить площадь области, ограниченной кривыми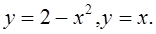

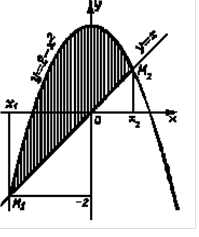
Р е ш е н и е.

Определим точки пересечения данных кривых. В точке пересечения ординаты равны, т. е. 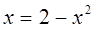, отсюда 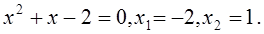Мы получили две точки пересечения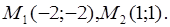

Следовательно, искомая площадь

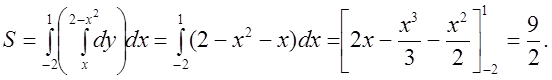(ед²)