Часть 1. Функциональные ряды

Московский Государственный Технический Университет

Имени Н.Э. Баумана

Дубограй И.В., Дьякова Л.Н., Скуднева О.В.

Степенные ряды.

Методические указания к выполнению типового расчёта.

Москва

Издательство МГТУ им. Н.Э. Баумана

Рецензент М.М.Сержантова

Дубограй И.В., Дьякова Л.Н., Скуднева О.В.

Степенные ряды: Методические указания к выполнению типового расчёта.-

М.: Изд-во МГТУ им. Н.Э. Баумана, 2005, -43с.

Ирина Валерьевна Дубограй

Людмила Николаевна Дьякова

Оксана Валентиновна Скуднева

Степенные ряды

Тираж 1500 экз.

Введение.

Данные методические указания предназначены для работы студентов второго курса всех специальностей при изучении темы «Степенные ряды», а также содержат варианты домашнего задания.

В работе кратко изложены все необходимые для решения задач сведения из теории, подробно разобраны решения типовых задач, особое внимание уделено тем частям решения, где студенты чаще всего допускают ошибки при выполнении домашнего задания.

Данная работа позволит студентам успешно изучить соответствующий раздел математики и справиться с выполнением домашнего задания.

После каждого раздела даны задачи с ответами для самостоятельной работы, которая позволит студентам выяснить, насколько хорошо усвоен материал.

Указания можно использовать как для самостоятельной работы, так и для проведения занятий в аудитории.

Часть 1. Функциональные ряды.

Определение.Ряд 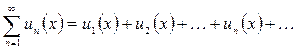(1.1),

где 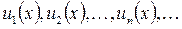являются функциями переменной x, называется функциональным рядом. Подставляя в этот ряд конкретное числовое значение 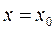, мы получим числовой ряд

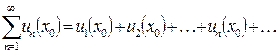, который может оказаться как сходящимся, так и расходящимся.

Определение. Совокупность всех значений переменной x, для которых получающиеся числовые ряды сходятся, называется областью сходимости функционального ряда (1.1).

Пример 1.1.Найти область сходимости функционального ряда .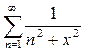

При любом фиксированном x получаем знакоположительный ряд. Необходимый признак сходимости выполняется при любом x: .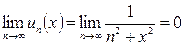

В качестве достаточного применим признак сравнения с рядом Дирихле 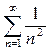. Очевидно, что при любом x выполняется неравенство .

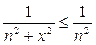Ответ: область сходимости данного ряда .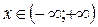

Пример 1.2.Найти область сходимости функционального ряда .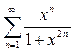

Проверим, при каких значениях переменной x выполняется необходимый признак сходимости:

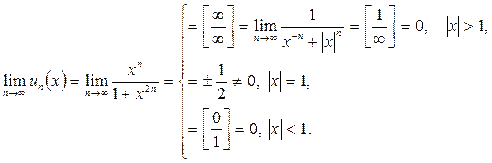
Необходимый признак выполняется при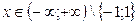

Применим радикальный достаточный признак Коши к ряду из модулей.

а) Если 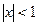, то ,

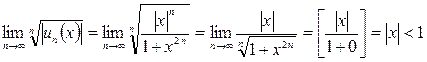т.е. при 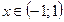ряд сходится абсолютно.

б) Если 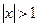, то ,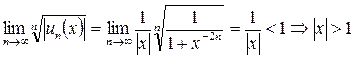

т.е. при 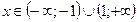ряд сходится абсолютно.

Ответ: область абсолютной сходимости ряда: .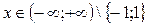

Если значение 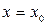принадлежит области сходимости функционального ряда 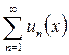, то говорят о сумме этого функционального ряда в точке 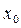: 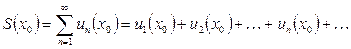(1.2). Таким образом, значение суммы функционального ряда зависит от значения 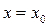, то есть, сумма функционального ряда сама является функцией, областью определения которой является область сходимости функционального ряда. Значит, можно говорить о её непрерывности, дифференцировании, интегрировании а, следовательно, и о таких же операциях над членами ряда, который сходится к данной функции .

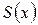Сходимость ряда (1.2) к числу 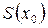означает, что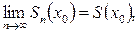

где 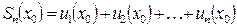- n-ая частичная сумма ряда (1.2).

Другими словами, для любого 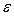>0 найдётся такое число 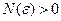, что для всех n>N( 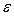) выполняется неравенство: 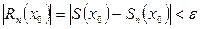, (1.3) где 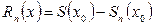- называется остатком ряда (1.2).

Если ряд 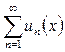сходится для всех значений из некоторого множества, то каждому значению x будет соответствовать свой числовой ряд и своё число N, при котором будет выполняться неравенство (1.3). Следовательно, 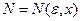, то есть величина, зависящая от выбора 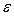и x.

Определение. Функциональный ряд 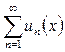называется равномерно сходящимся в некоторой области D, если он сходится для всех x из этой области, и для любого 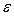>0 существует такое число 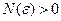, зависящее от

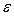, но не зависящее от x, что для всех n>N( 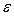) выполняется неравенство 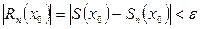для любого x из рассматриваемой области.

Часть 2. Степенные ряды.