Аксиоматическое построение теории вероятностей. Следствия из аксиом

Аксиома 1:Каждому случайному событию А поставлено в соответствие неотрицательное число Р(А), называемое его вероятностью

Аксиома 2: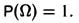

Аксиома 3: Если события ААА попарно несовместимы, то

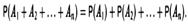
Из сформулированных аксиом можно вывести несколько важных элементарных следствий:

Из 1-й:

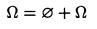
Из 3-й:

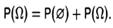
Таким образом:

1) Вероятность невозможного события равна нулю

2) Для любого события А

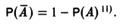
3) Каково бы ни было случайное событие А

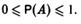
4) Если событие А влечёт за собой событие В, то

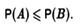
5) Пусть А и В — два произвольных события. Т. к. в суммах А + В = А + (В – АВ) и В = АВ + (В – АВ) слагаемые являются несовместимыми событиями, то в соответствии с аксиомой 3:

Р(А + В) = Р(А) + Р(В – АВ); Р(В) = Р(АВ) + Р(В – АВ)

Отсюда вытекает теорема сложения для произвольных событий А и В:

Р(А + В) = Р(А) + Р(В) – Р(АВ)

В силу неотрицительности Р(АВ) отсюда заключаем, что

Р(А + В) 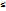Р(А) + Р(В)

71. Случайная величина называется Дискретной , если множество ( x1 ,x2 …….. Xm……..) её возможных значений конечно или счётно ( т.е. если все её значения можно перечислить).

При решении задач на составление ряда распределения дискретной СВ нужно отвечать на следующие вопросы:Каковы возможные значения этой СВ?В чём заключается событие ( пси = Х₀?Как определить вероятность таких событий?Дискретная СВ (пси) имеет Распределение Пуасона с параметром a, если она принимает значения 0, 1, 2……., m ……. . Закон распределения Пуасона является хорошим приближением для биномиального распределения при больших значениях n и p ( или 1 – p).

СВ (пси) имеет Бинамиальное распределение с параметрами n и p , если она принимает значения 0 , 1 , ……. n с вероятностями P( пси = m)= C_n^m p^mq^n-m, m = 0 1 2 …… , n, где 0<p<1 , q = 1 –p .

72. СВ называется Непрерывной,если её функция распределения непрерывна на всей числовой оси . Непрерывная СВ принимает все значения из некоторого интервала или системы интервалов на числовой оси.

1)Непрерывная СВ (пси) имеет Равномерное распределение на отрезке (А:B), если её плотность распределения постоянна на этом отрезке, а вне его равна нулю:

P(х) = 1/b-a при x € [a;b]

P(х) = 0 при Х не принадлежит [а,б]

2)Непрерывная СВ( пси) имеет Показательное (экспоненциальное) распределение с параметром Лямда > 0 , если её плотность распределения имеет вид: P(х) = лямда e ^{–лямда х} при Х≥0

P(х) = 0 при Х < 0.

73. Функции распределения случайной величины и её свойства. Определение случайной величины.

Функция распределения представляет собой универсальный способ задания СВ в том смысле ,что она существует для любой СВ. Ряд распределения существует только для дискретной СВ, а плотность распределения ----- только для непрерывной. Для непрерывной СВ функция распределения F(х) = P((пси)<х) непрерывна в любой точке числовой прямой. Более того, P((пси)=х₀)=0, т.е вероятность того , что непрерывная СВ примет заранее указанное значение, равна нулю.( Заметим , однако, что это событие не обязательно невозможно.) Отсюда следует, что для непрерывной СВ P (α ≤ (пси) ≤ β) = P(α < (пси) ≤ β) = P(α< (пси) <β) = P(α ≤ (пси)) <β = F(β) – F(α).

74. Свойство плотности распределения случайной величины. Примеры. Ряд распределения. Функцию p(x) будем называть Плотностью распределения СВ (пси), если вероятность того , что (пси) принимает значения из промежутка (-∞; х) равна интегралу от этой функции в пределах от -∞ до х , т.е F(x) = P( (пси) < x) = 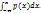Следовательно если функция p(x) непрерывна в точке х, то функция распределения F(x) дифференцируема в этой точке, причём p(x) = F(x). Свойства плотности распределения .1. p(x) ≥ 0 при всех Х , т.к F(x) ----- неубывающая функция. 2 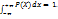Вероятность попадания непрерывной СВ (пси) в интервал , отрезок или полуинтервал с одними и теми же концами одинаковы и равны определённому интегралу от плотности вероятности на этом промежутке : P (α ≤ (пси) ≤ β) = P(α < (пси) ≤ β) = P(α< (пси) <β) =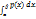

75. Математическое ожидание М(пси) и дисперсия D(пси) непрерывной СВ (пси) определяется по формулам M(пси) = 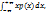D(пси) = 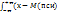²p(x)dx. На практике вычесления дисперсии, как правило , удобно использовать формулу M(пси²) = 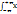²p(x) dx.

Свойства:
1. Математическое ожидание постоянной С равно этой постоянной.
2. Постоянный множитель можно выносить за знак математического ожидания, т.е. 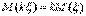3. Математическое ожидание суммы нескольких случайных величин равно сумме математических величин: 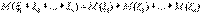4. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин **: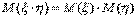

76. Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

1°. Дисперсия постоянной равна нулю.
2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: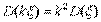

3. Есл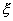и и 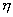- независимые случайные величины , то дисперсия суммы этих величин равна сумме их дисперсий:

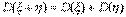4. Дисперсия любой случайной величины неотрицательна: 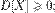Среднеквадратическим отклонением случайной величины Х называется квадратный корень из дисперсии.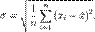

77. Числовые характеристики СВ:

1. Дисперсия; 2. Мат. ожидание; 3. Начальный; 4. Центральный момент.

Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x , т.е. a _k = Mx ^k.

Центральным моментом k-го порядка случайной величины x называется величина m _k, определяемая формулой m _k = M(x - Mx )^k.

Заметим, что математическое ожидание случайной величины - начальный момент первого порядка, a ₁ = Mx , а дисперсия - центральный момент второго порядка,

a ₂ = Mx ² = M(x - Mx )² =Dx .

78. Нормальное распределение (распределение Гаусса) — распределение вероятностей, которое задается функцией плотности распределения: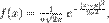

Правило трех сигм: Вероятность того, что случайная величина отклонится от своего математического ожидания на большую величину, чем утроенное среднее квадратичное отклонение, практически равна нулю. практически все значения нормально распределённой случайной величины лежат в интервале 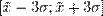.