Линейная зависимость и независимость системы векторов

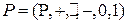- поле скаляров, 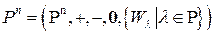- арифметическое 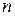- мерное векторное пространство, где .

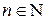Определение. Пусть 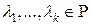, 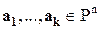. Линейной комбинацией векторов 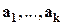с коэффициентами 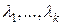называется вектор: .

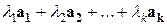Пример. Для векторов 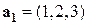; 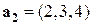вычислить линейную комбинацию

.

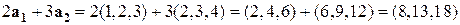Определение. Система векторов 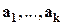называется линейно независимой тогда и только тогда, когда для любых скаляров 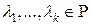из равенства .

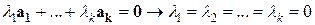Другими словами, система векторов 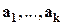линейно независима тогда и только тогда, когда из равенства линейной комбинации этих векторов нулевому вектору, следует, что все коэффициенты равны числу нуль.

Определение. Система векторов 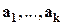называется линейно зависимой тогда и только тогда, когда существуют 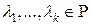, такие, что ( 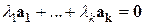) и не все скаляры 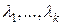равны нулю.

Другими словами, система векторов 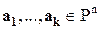линейно зависима тогда и только тогда, когда существуют скаляры не все равные нулю, такие, что линейная комбинация векторов с этими коэффициентами равна нулевому вектору.

Из определения следуют два утверждения.

1) Если система векторов 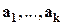не является линейно независимой, то она линейно зависима, и наоборот.

Доказательство. 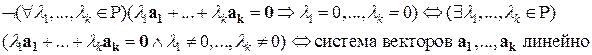зависима.

■

2) Система векторов 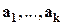- линейно зависима тогда и только тогда, когда уравнение 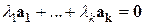имеет ненулевое решение, то есть .

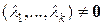Пример 1. Будет ли система векторов 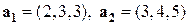из 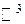линейно зависима или линейно независима?

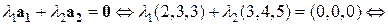
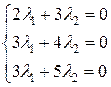
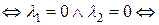векторы 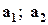линейно независимы.