Неопределенные и определенные интегралы 1 страница
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МАРИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
НЕОПРЕДЕЛЁННЫЙ И ОПРЕДЕЛЁННЫЙ
ИНТЕГРАЛЫ
Типовой расчет
Йошкар-Ола
УДК 51.517.3 (07)
Неопределённый и определённый интегралы: Типовой расчет / Сост. Ю.А.Фомина, Л.Н.Шарафутдинова. - Йошкар-Ола: МарГТУ, 2004.- 84с.
Приведены 40 вариантов заданий, составленных в соответствии с учебным планом по разделу «Неопределённые и определённые интегралы».
Для студентов 1 курса
Печатается по решению
редакционно-издательского совета МарГТУ
Рецензент: заведующий кафедрой математического анализа и теории функции МарГУ, кандидат физ.-мат. наук, доцент В.П. Микка
© МарГТУ, 2004
Порядок выполнения и защиты типового расчета
1. Выполнение и защита типового расчета проводится по графику самостоятельной работы студентов.
2. Все задачи должны быть решены письменно и подробно. Нумерация задач должна совпадать с их номером в типовом расчете.
3. Во время защиты типового расчета студент должен уметь отвечать на теоретические вопросы, пояснять решения задач, решать задачи аналогичного типа.
4. Типовой расчет следует выполнять в отдельной тетради. Первая страница оформляется по следующему образцу:
| Марийский государственный технический университет Неопределённый и определённый интегралы ТИПОВОЙ РАСЧЕТ студента(ки) факультета____________________________________ наименование факультета специальности_____________________________ группы_________ наименование специальности № группы _________________________________________________________ Ф.И.О. полностью |
Вариант 1.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
а)  ; | б)  . |
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; | б)  . |
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а)  dx; | б)  . |
4. Найдите неопределённые интегралы от тригонометрических функций:
а)  ; | б)  . |
5. Найдите неопределённые интегралы:
а)  ; | б)  . |
6. Найдите неопределённые интегралы от дробно-рациональных функций:
а)  ; | б)  dx. |
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
а)  ; | б)  . |
8. Вычислите определённый интеграл :
a)  ; | б)  . |
9. Вычислите определённый интеграл, используя формулу интегрирования по частям:
.
10. Вычислите определённый интеграл, используя указанную замену переменной:
, 
.
11. Вычислите несобственные интегралы либо докажите их расходимость:
a)  ; | б)  . |
12. Вычислите площадь фигуры, ограниченной линиями:
а) 
, 
;
б) прямыми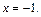 
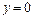и графиком функции
.
Вариант 2.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
а)  ; | б)  . |
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; | б)  . |
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а)  ; | б)  . |
4. Найдите неопределённые интегралы от тригонометрических функций:
а)  ; | б)  . |
5. Найдите неопределённые интегралы:
а)  ; | б)  . |
6. Найдите неопределённые интегралы от дробно-рациональных функций:
а)  ; | б)  dx. |
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
а)  ; | б)  . |
8. Вычислите определённый интеграл :
a)  ; | б)  . |
9. Вычислите определённый интеграл, используя формулу интегрирования по частям:
.
10. Вычислите определённый интеграл, используя указанную замену переменной:
, 
.
11. Вычислите несобственные интегралы либо докажите их расходимость:
а)  ; | б)  . | |||
12. Вычислите площадь фигуры, ограниченной линиями:
а) 
,
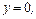
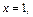
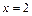б) прямыми 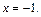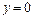и графиком функции
.
Вариант 3.
- Найдите неопределённые интегралы, непосредственно интегрируя:
а)  ; | б)  . |
- Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; | б)  . |
- Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а)  ; | б)  . |
- Найдите неопределённые интегралы от тригонометрических функций:
а)  ; | б)  . |
- Найдите неопределённые интегралы:
а)  ; | б)  . |
- Найдите неопределённые интегралы от дробно-рациональных функций:
а)  ; | б)  dx. |
- Найдите неопределённые интегралы, применив необходимую замену переменной:
а)  ; | б)  . |
- Вычислите определённый интеграл :
a)  ; | б)  . |
- Вычислите определённый интеграл, используя формулу интегрирования по частям:
.
- Вычислите определённый интеграл, используя указанную замену переменной:
, 
.
- Вычислите несобственные интегралы либо докажите их расходимость:
а)  ; | б)  . |
12. Вычислите площадь фигуры, ограниченной линиями:
а)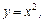 
,
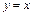б) прямыми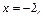 
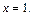
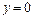и графиком функции
.
Вариант 4.
- Найдите неопределённые интегралы, непосредственно интегрируя:
а)  ; | б)  . |
- Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; | б)  . |
- Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а)  ; | б)  . |
- Найдите неопределённые интегралы от тригонометрических функций:
а)  ; | б)  . |
- Найдите неопределённые интегралы:
а)  ; | б)  . |
- Найдите неопределённые интегралы от дробно-рациональных функций:
а)  ; | б)  dx. |
- Найдите неопределённые интегралы, применив необходимую замену переменной:
а)  ; | б)  . |
- Вычислите определённый интеграл :
a)  ; | б)  . |
- Вычислите определённый интеграл, используя формулу интегрирования по частям:
.
- Вычислите определённый интеграл, используя указанную замену переменной:
, 
.
- Вычислите несобственные интегралы либо докажите их расходимость:
а)  ; | б)  . | |||
12. Вычислите площадь фигуры, ограниченной линиями:
а)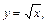 
,
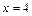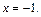
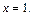
б) прямыми 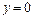и графиком функции
.
Вариант 5.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
а)  ; | б)  . |
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; | б)  . |
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а)  ; | б)  . |
4. Найдите неопределённые интегралы от тригонометрических функций:
а)  ; | б)  . |
5. Найдите неопределённые интегралы:
а)  ; | б)  . |
6. Найдите неопределённые интегралы от дробно-рациональных функций:
а)  ; | б)  dx. |
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
а)  ; | б)  . |
8. Вычислите определённый интеграл :
a)  ; | б)  . |
9. Вычислите определённый интеграл, используя формулу интегрирования по частям:
.
10. Вычислите определённый интеграл, используя указанную замену переменной:
, 
.
11. Вычислите несобственные интегралы либо докажите их расходимость:
а)  ; | б)  . | |||
12. Вычислите площадь фигуры, ограниченной линиями:
а)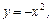 
,
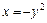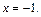
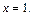
б) прямыми 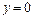и графиком функции
.
Вариант 6.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
а)  ; | б)  . |
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; | б)  . |
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а)  ; | б)  . |
4. Найдите неопределённые интегралы от тригонометрических функций:
а)  ; | б)  . |
5. Найдите неопределённые интегралы:
а)  ; | б)  . |
6. Найдите неопределённые интегралы от дробно-рациональных функций:
а)  ; | б)  dx. |
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
а)  ; | б)  . |
8. Вычислите определённый интеграл :
a)  ; | б)  . |
9. Вычислите определённый интеграл, используя формулу интегрирования по частям:
.
10. Вычислите определённый интеграл, используя указанную замену переменной:
, .
11. Вычислите несобственные интегралы либо докажите их расходимость:
а)  ; | б)  . | |||
12. Вычислите площадь фигуры, ограниченной линиями:
а)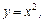 
,
б) прямыми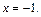 
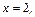
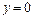и графиком функции
.
Вариант 7.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
а)  ; | б)  . |
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; | б)  . |