Элементы теория Марковских случайный процесс

Пусть система S имеет несколько составов, если состояние системы изменится случайно во времени заранее не предполагаемым образом, то говорят, что в системе происходит случайный процесс. Случайный процесс протекающий в системе, называется Марковским, если он обладает следующими свойствами.

Для каждого момента времени t_o вероятность любого сост. системы в будущем, то есть при t>t_o зависит только от её состояния в настоящем и не зависит от того, когда и каким образам система перешла в это состояние, то есть как развивался процесс в прошлом.

Случайные процессы могут быть с дискретными и непрерывными составами. Случайный процесс называется процессом с дискретным состояниями если возможное состоят системы S₁,S₂…….S_n можно перечислить, а сам процесс состоит в том, что система время от времени переходит из одного состояния в другое

При анализе случайных процессов с дискретными состояниями удобно пользоваться графиком состояний, который изображен

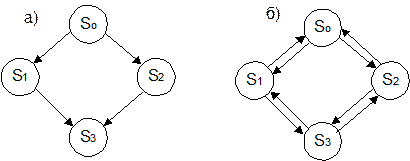
На рисунке а график состоянии для не восстанавливающейся системы, на рисунке б для восстанавливающейся системы

при этом учитывается, что отказавший узел начинает восстанавливаться немедленно после отказа. Переходом из S₀ в S₃ пренебрегают так как отказ второго узла маловероятен.

Способы математического описания Марковского случая процесса с дискретным составом зависит от того, в какие моменты времени, происходит переход системы и одного состояния в другое.

Случайный процесс – процесс с непрерывным временем. , если переход системы из состояния S_i →S_j возможен любой момент времени.

Случайный процесс называется процессом с дискретным временем, если переход системы из одного состояния в другое возможен только в строго определенный моменты времени. В теории надежности рассмотрим основные Марковские процессы с дискретными состояниями и непрерывным временем. времени.