Неполные уравнения плоскости

Уравнения прямой на плоскости

Прямая на плоскости и в пространстве.. Взаимосвязь различных видов уравнений прямой.

Рассмотрим различные виды уравнений прямой на плоскости.

Пусть прямая проходит через точку М₀ (x₀,y₀) перпендикулярно вектору n = {A,B}. Тогда вектор , где М(х,у) — произвольная точка прямой, ортогонален n. Поэтому координаты любой точки данной прямой удовлетворяют уравнению

А(х — х₀) + В(у — у₀) = 0 - (7.3)

уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Замечание. Вектор n называется нормалью к прямой.

Преобразуем уравнение (7.3) к виду:

Ах + Ву + (-Ах₀ — Ву₀) = 0.

Обозначив -Ах₀ — Ву₀ = С, получим общее уравнение прямой:

Ах + Ву + С = 0. (7.4)

Получим теперь уравнение прямой, проходящей через точку М₀ (x₀,y₀) параллельно вектору q = {l,m}. Так как вектор , где М(х,у) — произвольная точка прямой, коллинеарен q, координаты любой точки данной прямой удовлетворяют уравнению

, (7.5)

называемому каноническим уравнением прямой. Вектор q при этом называется направляющим вектором прямой. В частности, если прямая проходит через точки М₁(х₁,у₁) и М₂(х₂,у₂), ее направляющим вектором можно считать , и из уравнения (7.5) следует:

- (7.6)

параметрические уравнения прямой.

Для прямой l, не параллельной оси Оу, можно ввести так называемый угловой коэффициент k — тангенс угла, образованного прямой и осью Ох, и записать уравнение

у l прямой в виде:

у = kx + b - (7.8)

Прямая и плоскость в пространстве. Уравнения плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямой и плоскостью.

Отметим, что многие утверждения и формулы, касающиеся плоскости в пространстве, доказываются и выводятся так же, как при изучении прямой на плоскости, поэтому в этих случаях будут даваться ссылки на предыдущую лекцию.

Плоскость в пространстве.

Получим сначала уравнение плоскости, проходящей через точку М₀(х₀ ,у₀ ,z₀) перпендикулярно вектору n= {A,B,C},называемому нормалью к плоскости. Для любой точки плоскости М(х, у, z) вектор М₀М = {x - x₀ , y - y_{0 ,} z - z₀) ортогонален вектору n, следовательно, их скалярное произведение равно нулю:

A(x - x₀) + B(y - y₀) + C(z - z₀) = 0. (8.1)

Получено уравнение, которому удовлетворяет любая точка заданной плоскости — уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

После приведения подобных можно записать уравнение (8.1) в виде:

Ax + By + Cz + D = 0, (8.2)

где D = -Ax₀ - By₀ - Cz₀. Это линейное уравнение относительно трех переменных называют общим уравнением плоскости.

Неполные уравнения плоскости.

Если хотя бы одно из чисел А, В, С, D равно нулю, уравнение (8.2) называют неполным.

Рассмотрим возможные виды неполных уравнений:

1) D = 0 — плоскость Ax + By + Cz = 0 проходит через начало координат.

2) А = 0 — n = {0,B,C}Ox, следовательно, плоскость By + Cz + D = 0 параллельна оси Ох.

3) В = 0 — плоскость Ax + Cz +D = 0 параллельна оси Оу.

4) С = 0 — плоскость Ax + By + D = 0 параллельна оси Оz.

5) А = В = 0 — плоскость Cz + D = 0 параллельна координатной плоскости Оху (так как она параллельна осям Ох иОу).

6) А = С = 0 — плоскость Ву + D = 0 параллельна координатной плоскости Охz.

7) B = C = 0 — плоскость Ax + D = 0 параллельна координатной плоскости Оуz.

8) А = D = 0 — плоскость By + Cz = 0 проходит через ось Ох.

9) B = D = 0 — плоскость Ах + Сz = 0 проходит через ось Оу.

10) C = D = 0 - плоскость Ax + By = 0 проходит через ось Oz.

11) A = B = D = 0 — уравнение Сz = 0 задает координатную плоскость Оху.

12) A = C = D = 0 — получаем Ву = 0 — уравнение координатной плоскости Охz.

13) B = C = D = 0 — плоскость Ах = 0 является координатной плоскостью Оуz.

Если же общее уравнение плоскости является полным ( то есть ни один из коэффициентов не равен нулю), его можно привести к виду: (8.3) называемому уравнением плоскости в отрезках. Способ преобразования показан в лекции 7. Параметры а, b и сравны величинам отрезков, отсекаемых плоскостью на координатных осях.

Всякая плоскость в пространстве, снабженном декартовой системой координат, есть множество вех точек, удовлетворяющих некоторому линейному уравнению вида: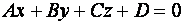

Всякую плоскость в пространстве можно задать, указав какую – ни будь ее точку и два произвольных приложенных к этой точке неколлинеарных вектора: 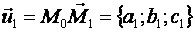и .

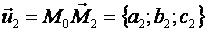-векторноеур-е плоскости.

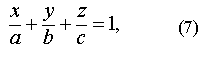
(7)- Уравнение (7) называют уравнением плоскости в отрезках на осях, т.к. числа a, b, c имеют простой геометрический смысл: а - абсцисса точки пересечения плоскости с осью Ох, b - ордината точки пересечения плоскости с осью Оу, с - аппликата точки пересечения плоскости с осью Oz.

-параметрическое уравнение прямой :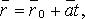

где 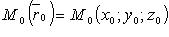- фиксированная точка, лежащая на прямой; 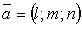-направляющий вектор.

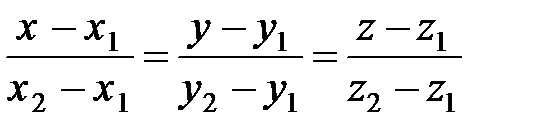- это называют уравнениями прямой, проходящей через две заданные точк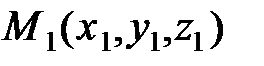и и .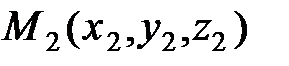

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A₁ x + B₁ y + C₁ z + D₁ = 0, A₂ x + B₂ y + C₂ z + D₂ = 0;

2) двумя своими точками M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), тогда прямая, через них проходящая, задается уравнениями:

=

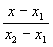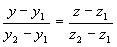
3) точкой M₁(x₁, y₁, z₁), ей принадлежащей, и вектором a(m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

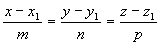
ВИДЫ УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ:

Уравнение прямой с угловым коэффициентом:y= kx + b

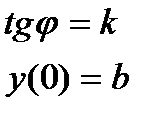
Уравнение прямой в отрезках: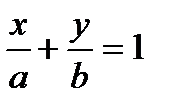

Общее уравнение прямой: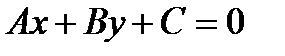

Уравнение с данным направляющим вектором и проходящей через данную точку:

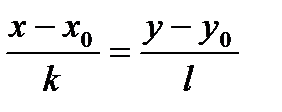
Уравнение прямой с данным вектором нормали

и проходящей через данную точку: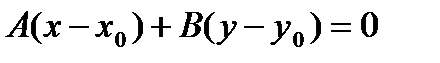

Билет 23. Взаимное расположение плоскостей

Возможны два случая взаимного расположения двух плоскостей в пространстве:

• Параллельны

• Пересекаться

Опр. Две плоскости в пространстве называются параллельными, если они не пересекаются, в противном случае они пересекаются.

Теорема1:Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство:

Пусть и – данные плоскости, а1 и а2 - прямые в плоскости , пересекающиеся в точке А, в1 и в2 – соответственно параллельные им прямые в

плоскости . Допустим, что плоскости и не параллельны, т.е. пересекаются по некоторой прямой с. По теореме прямые а1 и а2, как параллельные прямым в1и в2, параллельны плоскости , и поэтому они не

пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости через точку А проходят две прямые (а1 и а2) , параллельные прямой с. Но это невозможно по аксиоме параллельных. Мы пришли к противоречию ЧТД.

Перпендикулярные плоскости: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Теорема2: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство:

Пусть - плоскость, в –перпендикулярная ей прямая, - плоскость, проходящая через прямую в, с - прямая, по которой пересекаются плоскости и . Докажем, что плоскости и перпендикулярны. Проведем в плоскости через точку пересечения прямой в с плоскостью прямую а, перпендикулярную прямой с. Проведем через прямые а и в плоскость . Она перпендикулярна прямой с, т.к.прямая с перпендикулярна прямым а и в. Т. к. прямые а и в перпендикулярны, то плоскости и перпендикулярны. ч.т.д.

Необходимым и достаточным условием пересечения двух плоскостей (4.22) является условие не коллинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:

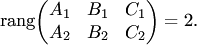
При этом условии система уравнений 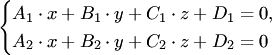имеет бесконечно много решений, которые определяют прямую пересечения плоскостей, заданных уравнениями.

Угол между двумя плоскостями можно определить как угол между их нормальными векторами. Поэтому определению получаются не один угол, а два смежных угла, дополняющих друг друга до 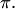В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е.величина 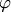угла между двумя плоскостями удовлетворяет условию 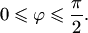Если 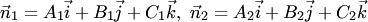— нормали к плоскостям 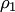и 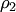соответственно (рис.4.20,а), то величина 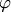угла между этими плоскостями вычисляется по формуле:

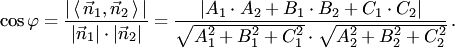
Билет 24.Взаимное расположение прямых

Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны. Прямые заданы уравнениям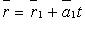и и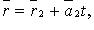

1. Пересекающиесяпрямые

Пересекающимися прямым и называются такие прямые, которые имеют одну общую точку.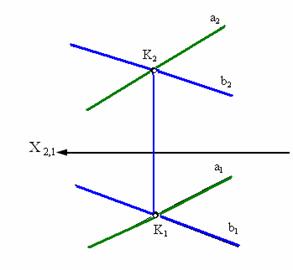

2. Параллельные прямые

Параллельные прямые – прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке). .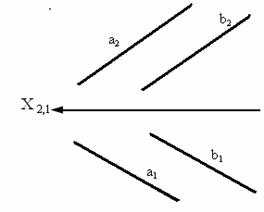

3. Скрещивающиеся прямые

Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки. .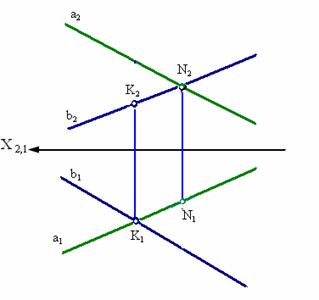

Билет 25. Задачина прямую и плоскость

Довольно часто встает следующая задача.Требуется от общих уравнений прямой перейти к параметрическим, которые в некотором смысле являются более удобными. Для того, чтобы написать параметрические уравнения прямой нужно знать координаты какой-нибудь точки на прямой и координаты направляющего вектора. Прямая задана уравнениями 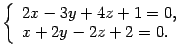Требуется написать ее параметрические уравнения. Найдем какую-нибудь точку 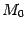на прямой. Положим 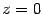.Система примет вид 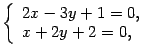Решая ее, находим , .

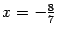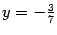Таким образом, на прямой лежит точка 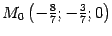.Найдем направляющий вектор. Нормальными векторами плоскостей, соответствующих уравнениям системы ,являются 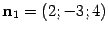, 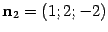. Положим 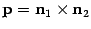. Тогда

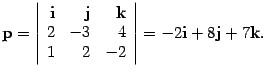Теперь, зная точку и направляющий вектор, можно написать параметрические уравнения прямой.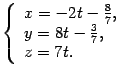

Следующая, часто встречающаяся, задача такая:

Дано уравнение плоскости и уравнения прямой. Требуется найти их точку пересечения.

Так как точка пересечения принадлежит и прямой, и плоскости, то она удовлетворяет и уравнению плоскости, и уравнениямпрямой. Поэтому для решения задачи нужно объединить уравнение плоскости и уравнения прямой в одну систему и решить ее.

ПримерНайдите точку пересечения прямой 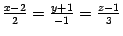и плоскости 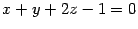. Прямая задана каноническими уравнениями. Им соответствует система уравнений 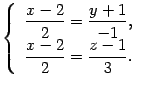В результате для нахождения точки пересечения прямой и плоскости получаем систему уравнений 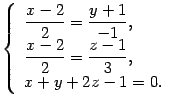Для ее решения можно предложить следующий путь. Из первого уравнения выражаем 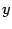через 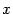: 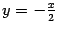. Из второго -- 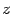через 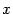: 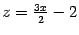. Найденные выражения для 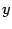и 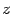подставляем в третье уравнение и находим 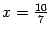.Находим 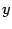и : , .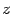

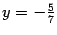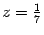Даны уравнения двухпрямых. Требуется найти угол между этими прямыми.

Следующие две задачи связаны с нахождением угла. Угол 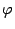между прямыми – это угол 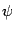между их направляющими векторами, если направляющие векторы образуют острый угол 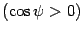,или 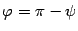, если 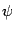-- тупой угол 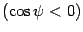. Во втором случае 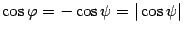.Для решения задачи достаточно найти направляющие векторы 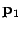и 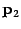прямых. Тогда 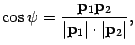а искомый угол 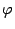определяется из равенства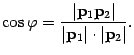

Билет 26. Расстояние от точки до плоскости

Пусть плоскость 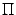задана уравнением 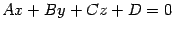и дана точка 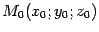.Тогда расстояние 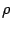от точки 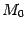до плоскости 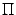определяется по формуле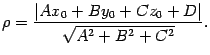

Доказательство. Расстояние от точки 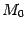до плоскости 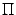-- это, по определению, длина перпендикуляра 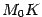,опущенного из точки 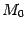на плоскость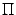

Вектор 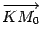и нормальный вектор nплоскости 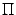параллельны, то есть угол 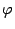между ними равен 0 или 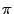,если вектор nимеет направление противоположное, указанному на рис. 11.9. Поэтому 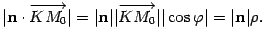Откуда 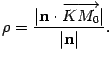Координаты точки 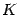,которые нам неизвестны, обозначим 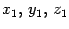. Тогда 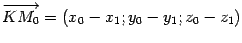.Так как 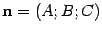,то 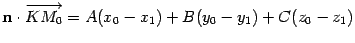. Раскрыв скобки и перегруппировав слагаемые, получим 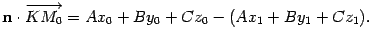Точка 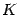лежит на плоскости 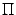,поэтому ее координаты удовлетворяют уравнению плоскости: 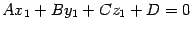. Отсюда находим, что .

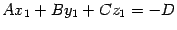27,28,29.Кривые второго порядка на плоскости: эллипс и его свойства

Кривые второго порядка на плоскости: гипербола и ее свойства

Кривые второго порядка на плоскости: парабола и ее свойства