Методы теории марковских процессов

В последние годы широкое распространение получили ме­тоды статистического анализа, оценивания и оптимального управ­ления стохастическими системами, основанные на использовании результатов теории марковских процессов. В данном разделе рас­сматривается применение методов теории марковских процессов для статистического анализа линейных и нелинейных стохастиче­ских систем.

Уравнение Фоккера — Планка — Колмогорова. В теории мар­ковских процессов получены дифференциальные уравнения в част­ных производных параболического типа для условной (переходной) 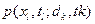и безусловной 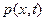плотностей распределения ве­роятностей непрерывного марковского процесса x(t). Применитель­но к скалярному марковскому процессу x(t) уравнение для плот­ности 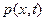, называемое уравнением Фоккера — Планка — Кол­могорова (ФПК), имеет вид

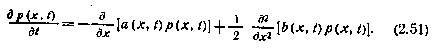
Функции а(х, t) иb(x, t) называют соответственно коэффициен­тами сноса и диффузии марковского процесса x(t).

В многомерном случае уравнение ФПКдля 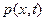векторного марковского процесса x(t), состоящего из п компонент 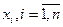, записывается следующим образом:

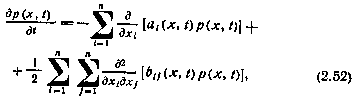
где 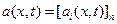— вектор коэффициентов сноса; 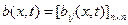—матрица коэффициентов диффузии векторного процесса x(t).

Интегрируя уравнение ФПК при заданном начальном условии 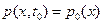, можно определить плотность распределения вероят­ностей 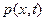рассматриваемого марковского процесса в последую­щие моменты времени.

Стохастические дифференциальные уравнения.Среди различных непрерывных марковских процессов в практических задачах осо­бенно большое значение имеют так называемые диффузионные марковские процессы, изменение которых во времени описывается дифференциальными уравнениями вида

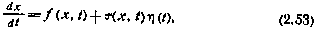
где 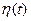—стандартный белый шум.

Такие уравнения называют стохастическими дифференциальны­ми уравнениями.

Уравнение вида (2.53) можно записать непосредственно для изу­чаемой динамической системы, если случайное входное воздействие этой системы действительно может быть аппроксимировано стан­дартным белым шумом. Например, одномерной системе, состоящей из интегрирующего звена 1/p, охваченного нелинейной обратной связью f(x), подверженной воздействию белого шума 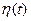на вхо­де, соответствует стохастическое дифференциальное уравнение пер­вого порядка

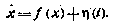
Используя метод формирующих фильтров, к виду (2.53) можно привести уравнения, описывающие поведение систем, подвержен­ных воздействию окрашенных шумов.

Пример. Пусть исследуемая динамическая система описывается передаточ­ной функцией апериодического звена

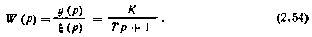
Внешнее воздействие 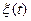—случайный процесс со спектральной плотностью

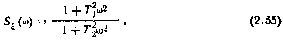
Коэффициент усиления К является гауссовской случайной величиной, харак­теризуемой параметрами m_k и D_k.

Чтобы описать эту систему стохастическим дифференциальным уравнением, перепишем соотношение (2.54) в виде дифференциального уравнения в нормаль­ной форме:

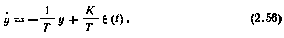
Последнее уравнение объединим с уравнением формирующего фильтра для 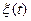, полученные ранее [см. формулу (2.30')].

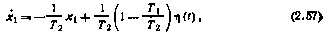
где

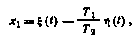
и уравнением формирующего фильтра для случайного параметра

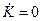(2.58)

В результате получим стохастическое дифференциальное уравнение вида (2.53), описывающее рассматриваемую динамическую систему, в котором векторный случайный процесс x(t), объединяющий в качестве составляющих переменные у, x₁ и К, есть диффузионный марковский процесс. Компоненты вектор-функции f^T(x, t) — [f_i(x, t)]_n в данном случае равны

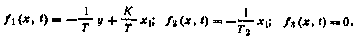
Белый шум 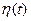является скалярным случайным процессом, поскольку в; правые части уравнений (2.56) и (2.57) входит одно и то же внешнее случай­ное воздействие, а

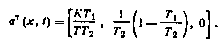
Возникает вопрос, как выражаются коэффициенты сноса а(х, t) и диффузии b(x, t), входящие в уравнение ФПК (2.51) или (2.52),. описывающие изменение плотности р(х, t) распределения вероят­ностей диффузионного марковского процесса x(t), через f(x, t) и 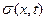? В зависимости от ответа на этот вопрос различают сто­хастические дифференциальные уравнения Ито и Стратоновича_ В уравнении Ито в скалярном случае коэффициенты сноса и диф­фузии соответственно равны f(x, t) и 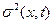. Для стохастического дифференциального уравнения Стратоновича эти коэффициенты определяются соотношениями *(* Диментберг М. Ф. Нелинейные стохастические задачи механических коле­баний. М.: Наука, 1980. 368 с.)

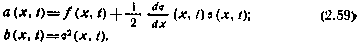
Конкретный вариант используемой интерпретации стохастиче­ского дифференциального уравнения зависит от особенностей ана­лизируемой физической системы.

В рассматриваемом далее в данной главе наиболее широко рас­пространенном случае, когда 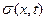не зависит от х, флуктуационная поправка к коэффициенту сноса, возникающая при рассмотре­нии стохастического дифференциального уравнения Стратоновича, обращается в нуль и обе интерпретации приводят к одним и тем же результатам.

Интегрировать аналитически и даже численно уравнение в част­ных производных параболического типа, каким является уравнение ФПК трудно, особенно в тех случаях, когда размерность вектора х велика. Только в одномерном и в отдельных двумерных случаях удается найти аналитическое решение этого уравнения, соответст­вующего стохастическому дифференциальному уравнению нелиней­ной системы. Однако каждое такое решение представляет большой интерес, поскольку оно является наиболее полной характеристикой точности системы, позволяющей оце­нить точность решений, полученных с помощью приближенных методов — расчета, например, с помощью ме­тода статистической линеаризации.

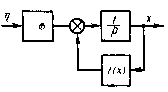
Рис. 2.1. Нелинейная система первого порядка.

Так, стационарным решением уравнения ФПК, соответствующего нелинейной системе первого порядка, показанной на рис. 2.4, для р(х,∞)=р_ст(х) является выражение [34]

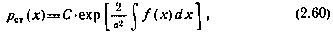
в котором постоянная интегрирования С выбирается из условия нормировки 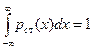. В случае стационарной линейной системы при f(x). = - х из (2.60) получаем гауссовскую плотность 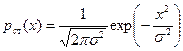. Если в обратной связи стоит реле с уровнем насыщения А, то

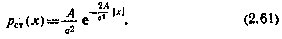
Плотности (2.61) соответствуют 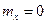и .

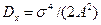Уравнения для моментов диффузионного процесса. Основным применением уравнения ФПК при априорном анализе точности си­стем является получение с его помощью обыкновенных дифферен­циальных уравнений для вектора математических ожиданий m_x(t) и корреляционной матрицы K_x(t) фазового вектора диффузионной марковской системы. Эти уравнения оказываются точными, если стохастическое дифференциальное уравнение (2.53) — линейное, и приближенными в случае нелинейного уравнения (2.53).

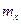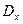Чтобы получить из уравнения ФПК уравнения для и в случае, когда x(t) —скалярный процесс, умножим (2.51) на х и про­интегрируем обе части по этой переменной в бесконечных пределах. Тогда получим

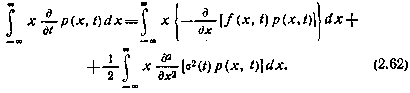
Слева в уравнении (2.62) имеем

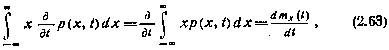
а интеграл справа вычисляем, применяя метод интегрирования по частям и учитывая граничные условия 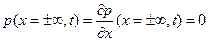. Окончательный результат оказывается следующим:

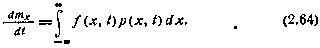
Уравнение для дисперсии D_x получают, умножив левую и пра­вую части (2.51) на 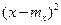и проинтегрировав их по перемен­ной х в бесконечных пределах. В итоге имеем

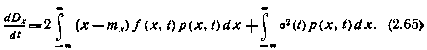
Соотношениями (2.64) — (2.65) устанавливается связь между производными по времени от m_x и D_x диффузионного процесса x(t) и его плотностью распределения р(х, t). Из них нельзя найти m_x(t) и D_x(t), если плотность р(х, t) неизвестна.

Уравнения для моментов в линейной системе. Если коэффициент сноса f(x, t) в правой части стохастического дифференциального уравнения (2.57) — линейный относительно х, т. е. f(x,t)=a(t)x + b(t), то соотношения (2.64) и (2.65) превращаются в уравнения относительно m_x и D_x, т. е. становятся замкнутыми. Действительно, в этом случае

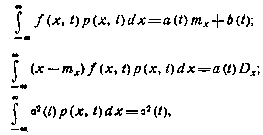
поэтому для линейной марковской системы первого порядка

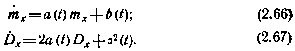
Интегрирование уравнений (2.66) и (2.67) при заданных на­чальных условиях m_x(t₀) и D_x(t₀) позволяет определить m_x(t) и D_x(t).

Если рассматриваемая система — стационарная и устойчивая, а искомыми являются m_x и D_x в установившемся режиме, то эти величины можно найти из алгебраических уравнений

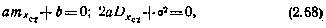
поскольку в установившемся режиме для такой системы 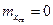и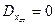

В многомерном случае уравнения для т_х и К_х оказываются сле­дующими:

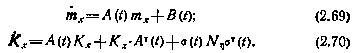
Векторное уравнение (2.69) размерности п совместно с матрич­ным уравнением (2.70) размерности п×п называют корреляцион­ной системой уравнений. Системы (2.69) и (2.70) не зависят друг от друга, поэтому их можно интегрировать раздельно. Учитывая симметричность матрицы К_х, Для ее определения достаточно про-янтегрировать п(п+1)/2 уравнений относительно различных кова­риационных моментов К_х. Начальными условиями для (2.69) и (2.70) являются вектор математических ожиданий m_x(t₀) и корре­ляционная матрица К_х (t₀) фазового вектора x(t₀) в начальный мо­мент времени.

Если исследуемая линейная марковская система — стационар­ная и устойчивая, а искомыми являются т_х и К_х в установившемся режиме, то их можно найти из систем алгебраических уравнений

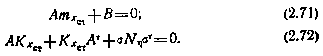
Одним из способов решения может служить интегрирование соответствующих им систем дифференциальных уравнений (2.69) и (2.70) при произвольно заданных начальных условиях. Сходи­мость решения обеспечивается устойчивостью исследуемой динами­ческой системы.

Приближенные уравнения для определения моментов диффузи­онного процесса в нелинейной системе.Для получения приближен­ной замкнутой системы уравнений из (2.64) и (2.65) в общем слу­чае нелинейного коэффициента сноса f(x, t) предположим, что плотность р(х, t) распределения вероятностей фазового вектора гауссовская. При р(х, t) =p_Г(x, t) интегралы в правых частях соот­ношений (2.64) и (2.65) можно вычислить. Результирующие функции зависят от m_x(t) и D_x(t), описывающих p_Г(x, t):

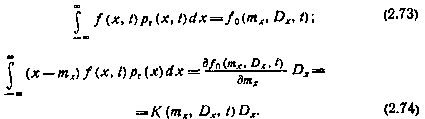
Подставив (2.73) и (2.74) в (2.64) и (2.65), получим систему из двух нелинейных обыкновенных дифференциальных уравнений:

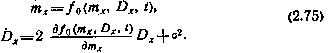
Интегрирование этой системы при заданных m_x(t₀) и D_x(t₀) позво­ляет найти m_x(t) и D_x(t), т. е. решить приближенно задачу стати­стического анализа рассматриваемой нелинейной системы. Для «типовых» нелинейностей f(x) формулы для f₀(m_x, D_x) и K(m_x, D_x) могут быть взяты из таблиц выражений коэффициентов статисти­ческой линеаризации.

Пример. Пусть f(x) в (2.53)—релейная характеристика f(x)=—A sign (x).

Для этой нелинейности f 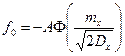(см. пример в разд. 1.1) и

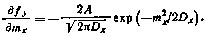
Уравнеиия для m_x и D_x в такой системе имеют вид

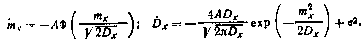
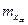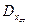Установившиеся значения и получаем, положив 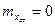и .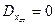

Имеем 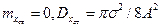. Сравнивая приближенное значение с точным, полученным ранее путем решения уравнения ФПК значением, видим, что предположение о гауссовском распределении р(х) в рассматриваемой нелиней­ной системе с реле в обратной связи приводит к ошибке в дисперсии, рав­ной 22%.

В многомерном случае вектор m_x(t) и корреляционную матрицу K_x(t) можно найти в результате совместного интегрирования двух систем обыкновенных дифференциальных уравнений

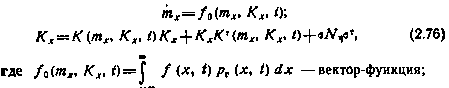
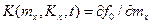— матричная функция, элементами которой являются частные производные от составляющих вектор-функции 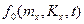по компонентам вектора т_х.

Если в состав исследуемой системы входят только линейные звенья и типовые одномерные существенные нелинейности, то кор­реляционную систему вида (2.76) удобно составить, применяя со­вместно статистическую линеаризацию нелинейных звеньев и кор­реляционную систему уравнений (2.69) — (2.70) для статистически линеаризованной системы.

Когда управляемое движение летательного аппарата описыва­ется нелинейными стохастическими дифференциальными уравне­ниями, правые части которых содержат гладкие многомерные не­линейности, приближенный анализ точности такого движения значительно упрощается по сравнению с непосредственным исполь­зованием уравнений (2.76), если пользоваться так называемой ква­зилинейной корреляционной системой уравнений. При составлении такой системы полное движение исследуемой системы разбивается на два движения: среднее и возмущенное. Для описания среднего движения, характеризующего изменение математических ожиданий составляющих фазового вектора, используются нелинейные урав­нения системы при математических ожиданиях (средних значениях) начальных условий и внешних воздействий. Для описания возму­щенного движения, характеризующего случайные отклонения со­ставляющих фазового вектора от их средних значений, применяют­ся линеаризованные уравнения, причем в качестве опорных значе­ний при линеаризации берутся математические ожидания фазовых координат в соответствующие моменты времени.

Пример.Рассмотрим задачу баллистического спуска летательного аппарата, т. е. спуска с нулевой подъемной силой, в атмосфере Земли. Продольное дви­жение аппарата описывается нелинейными дифференциальными уравнениями

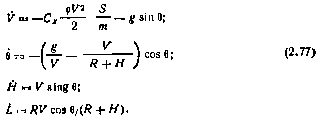
Требуется оценить рассеивание траекторий аппарата, предполагая случайными переменные V, θ, Н и L в момент t₀ начала спуска; постоянными величины R, С_х, S, т и g, а зависимость 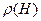—показательной вида 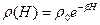, где .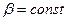

Перепишем уравнения движения аппарата в виде векторного уравнения

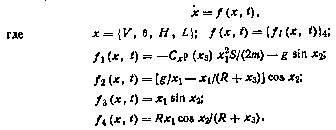
Представим фазовый вектор х в виде х=т_х+Δх, а нелинейную вектор-функ­цию f(x, t) линеаризуем в окрестности х=т_х:

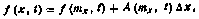
где 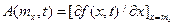—матрица 4×4 частных производных вектор-функции f(x, t) по составляющим вектора х, вычисленная при х=т_х. Получаем уравнение

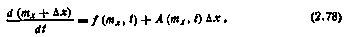
из которого в результате усреднения непосредственно находим уравнение для вектора математических ожиданий

по виду совпадающие с (2.77). Вычтя (2.79) из (2.78), получаем линеаризован­ное уравнение возмущенного движения

на основе которого составляем уравнение для корреляционной матрицы фазо­вого вектора

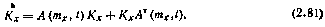
Совместное интегрирование уравнений (2.80) и (2.81), в совокупности образу­ющих квазилинейную корреляционную систему уравнений, при заданных на­чальных условиях т_х(t₀) и K_x(t₀) позволяет определить т_х(t) и Kx(t) в по­следующие моменты времени. Точность решения определяется точностью аппрок­симации вектор-функции линеаризованной зависимостью при тех значениях слу­чайных отклонений Δx (t) фазового вектора x(t), которые имеют место в рас­сматриваемой задаче при заданных статистических характеристиках случайных, начальных условий.

2.6. МЕТОД СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ (МОНТЕ-КАРЛО)

Метод статистического моделирования — универсальный метод статистического анализа стохастических систем (линейных и нелинейных, стационарных и нестационарных), подверженных воз­действию случайных факторов различных типов с произвольными их статистическими свойствами. В литературе данный метод также называют методом статистических испытаний или методом Монте-Карло.

Основу метода статистического моделирования составляет закон больших чисел, заключающийся в том, что результат усреднения, относящийся к случайному фактору (событию, величине, процессу или полю), вычисленный по п его реализациям, при 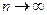перестает быть случайным и может рассматриваться в качестве оценки соответствующей характеристики рассматриваемого фактора. В част­ности, в соответствии с теоремой . Бернулли при большом числе опытов (реализаций) частота случайного события приближается к вероятности этого события. Аналогичные теоремы существуют и для статистических характеристик случайных величин, процессов, полей.

Применительно к априорному анализу точности стохастических систем метод статистического моделирования заключается в про­ведении на ЭВМ статистических экспериментов, имитирующих функционирование исследуемой системы при действии случайных факторов, и в последующей обработке полученных в этих экспери­ментах результатов с помощью методов математической статистики для определения соответствующих статистических характеристик.

Методика статистического моделирования. Первым этапом под­готовки к статистическому моделированию стохастической системы является выбор типа ЭВМ (ЦВМ, АВМ или аналого-цифрового комплекса), на которой целесообразно проводить моделирование. При этом учитываются сложность исследуемой системы, характер и число нелинейностей в ней, скорость протекания процессов в раз­личных частях (звеньях) системы, тип и характеристики действую­щих на систему случайных возмущений и другие факторы.

Выясняется возможность использования канонических разложе­ний случайных процессов, действующих на исследуемую систему. Если такие разложения известны для всех случайных функций, рас­сматриваемых в системе, моделирование системы можно заметно упростить, поскольку в этом случае при моделировании требуется получать реализации только случайных величин (начальных ус­ловий, параметров системы и коэффициентов канонических разло­жений).

Более общей и сложной является ситуация, когда в число воз­мущений системы входят случайные процессы, для которых канони­ческие разложения не известны. В этом случае описывающие ис­следуемую динамическую систему уравнения сводятся к системе стохастических дифференциальных уравнений в нормальной форме вида

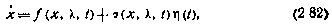
где λ — вектор случайных параметров системы; 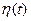— векторный белый шум. Вектор начальных условий x(t₀) также может быть случайным.

Некоторые из действующих на систему случайных возмущений могут оказаться не белым шумом. Для таких процессов требуется составить дифференциальные уравнения формирующих фильтров. Эти уравнения при моделировании следует интегрировать совмест­но с уравнениями системы (2.82).

Далее составляется программа интегрирования на ЦВМ систе­мы (2.82) совместно с уравнениями формирующих фильтров или схема моделирования для АВМ. Характерными элементами про­граммы являются блоки, обеспечивающие получение реализаций случайных факторов, рассматриваемых в системе.

Получение на ЭВМ реализаций случайных величин. При моде­лировании задачи на АВМ, а иногда и на ЦВМ реализации случай­ных величин задают с помощью таблиц случайных чисел. Наиболь­шее распространение получили таблицы случайных чисел, подчи­няющихся нормальному (гауссовскому) и равномерному распре­делениям. Таблица нормально распределенных случайных чисел содержит реализации гауссовской случайной величины 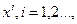соответствующие 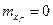и 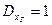.Беря числа из этой табли­цы, реализации 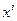гауссовской случайной величины с характери­стикам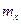и и 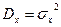вычисляют по формуле

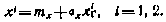
Таблица равномерно распределенных чисел содержит реализа­ции 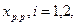подчиняющиеся равномерному на интервале [0,1] распределению вероятностей. Для получения реализаций величи­ны х, распределенной равномерно на интервале [X_min, X_max] числа 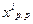, взятые из таблицы, преобразуют с помощью соотношения

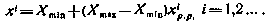
Основным способом получения реализаций случайных величин на ЦВМ является использование специальных стандартных подпро­грамм, называемых датчиками псевдослучайных чисел. При каж­дом обращении к датчику в нем вычисляется новое случайное чис­ло. Расчет проводится с помощью рекуррентной формулы, аргумен­тами которой являются несколько случайных чисел, вычисленных при предыдущих обращениях к данной подпрограмме. При фикси­рованной начальной (стартовой) совокупности случайных чисел все рекуррентно вычисляемые датчиком последующие числа будут определенными, зависящими от стартовой совокупности, поэтому числа, получаемые с помощью датчика, называют псевдослучайны­ми. Рекуррентная формула, реализованная в датчике, подбирается так, чтобы псевдослучайные числа, получаемые с помощью датчика, обладали требуемыми статистическими свойствами — соответство­вали определенной плотности распределения вероятностей р(х), а коэффициент корреляции был равен нулю.

Как правило, в библиотеке стандартных подпрограмм ЦВМ при­сутствуют два датчика псевдослучайных чисел: равномерно распре­деленных на интервале [0,1] и гауссовских с 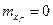и .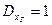

Получение реализаций векторной гауссовской случайной вели­чины затруднений не вызывает, если этот вектор некоррелирован. Реализации отдельных компонент такого вектора можно рассчиты­вать с помощью датчика гауссовских чисел независимо друг от друга. Если же гауссовский вектор х коррелирован, его реализации получают путем линейного преобразования реализаций некоррели­рованного гауссовского вектора U той же размерности, формируе­мого с помощью датчика гауссовских псевдослучайных чисел. У вектора U математическое ожидание — нулевой вектор, а корре­ляционная матрица — единичная. Матрица линейного преобразова­ния А подбирается так, чтобы результирующая ковариационная матрица К_х была равна заданной. При ее определении использу­ется соотношение (1.26).

При 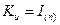из (1.26) получаем следующее уравнение относи­тельно А:

Это уравнение имеет бесчисленное множество решений. Если искать А в виде треугольной матрицы вида

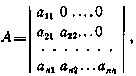
то из (2.83)получим n(n+1)/2 уравнений для элементов этой мат­рицы, которые можно решить рекуррентно. Результатом являются следующие выражения для элементов матрицы А:

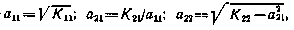
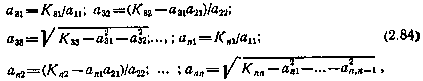
где 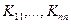— элементы заданной корреляционной матрицы .

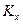Пример.Пусть х — двумерный вектор с корреляционной матрицей

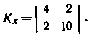
Найдем матрицу А, такую, что

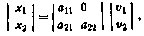
где 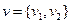—некоррелированный вектор с .

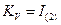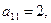
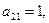
С помощью соотношений (2.84) находим ац 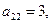т. е.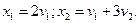

В ряде случаев требуется получать реализации случайной вели­чины, распределение которой не является ни равномерным, ни га-уссовским. Наиболее распространенным способом моделирования в данном случае является нелинейное преобразование реализаций, получаемых с помощью датчика равномерно распределенных чисел.

Задача определения нелинейного преобразования y=f(x), свя­зывающего случайные величины х и у с заданными плотностями распределения р(х) и р(у) (плотность р(х)—равномерная), яв­ляется обратной по отношению к задаче определения распределе­ния нелинейной функции случайной величины, рассмотренной в разд. 1.1. Если распределение р(х) — равномерное, то из соотно­шения (1.32) имеем 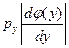, откуда при монотонно возрастаю­щей функции 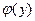получаем

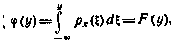
где F (у) — интегральная функция распределения вероятностей ве­личины у.

Функция 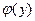является обратной по отношению к искомой функции f(x). Таким образом, определение искомого нелинейного преобразования y = f(x) сводится к нахождению по заданной плот­ности р(у) интегральной функции F(y) и последующему решению уравнения F (у) =х относительно у.

Пример.Пусть

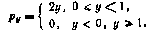
Тогда в интервале (0, 1) имеем xF(y)=y², откуда 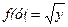,т. е. .

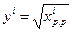Иной подход может быть применен в тех случаях, когда тре­буется получать реализации случайной величины у по имеющейся ее гистограмме или когда распределение р(у) имеет сложную фор­му, которую целесообразно аппроксимировать ступенчатой зависи­мостью.

Пусть интервал [у₀, у_п] практически возможных значений слу­чайной величины у, имеющей распределение р(у), разбит на п уча­стков 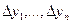, в пределах каждого из которых плотность р(у) можно полагать равномерной. Вероятность попадания в каждый интервал

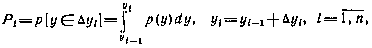
причем 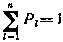. При использовании такой аппроксимации р(у)

реализацию 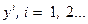можно определить в результате двукратного обращения к датчику равномерно распределенных псевдослучай­ных чисел. При первом обращении разыгрывается исход попадания реализации yⁱ в один из интервалов 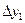. Для этого вероятностям P_l попадания yⁱ в интервалы 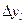ставятся в соответствие интервалы 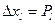значений равномерно распределенных псевдослучайных чи­сел из общего диапазона [0, 1]. Попаданию случайного числа хⁱ_р.р, получаемого в результате обращения к датчику, в интервал 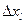ставится в соответствие попадание реализации yⁱ в интервал 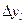. При втором обращении к датчику разыгрывается значение реали­зации yⁱ как случайной величины, распределенной равномерно в интервале .

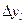Моделирование на ЭВМ реализаций случайных процессов.На АВМ реализации случайных процессов получают с помощью гене­раторов шума. Так называют электронный прибор, электрическое напряжение на выходе которого является случайным процессом с заданными статистическими характеристиками. Генераторы, ис­пользуемые при статистическом моделировании управляемого дви­жения летательных аппаратов, генерируют шум с равномерной спектральной плотностью в диапазоне инфранизких частот (от 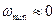до 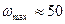Гц) и с гауссовским одномерным распределением вероятностей. При статистическом моделировании систем, по­лоса пропускания которых уже, чем 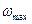, а именно такими, как правило, являются системы управления летательными аппаратами, шум генераторов можно считать белым. Окрашенные шумы, дей­ствующие на изучаемую систему, моделируют на АВМ путем про­пускания белого шума через соответствующим образом подобран­ный формирующий фильтр.

На ЦВМ белый шум моделируют, аппроксимируя его прибли­женно ступенчатым абсолютно случайным процессом x(t). Реали­зации последнего вычисляются по следующему правилу. Аргумент процесса — время t—изменяется дискретно с шагом Δt. В пределах каждого шага 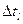значение реализации 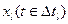задается заново с помощью датчика гауссовских псевдослучайных чисел

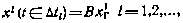
где В — постоянный множитель.

На всем интервале 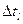значение 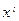остается постоянным. Псевдо­случайные числа, получаемые при помощи датчика, попарно некоррелированы друг с другом. Следовательно, корреляция между зна­чениями ступенчатого процесса x(t) в различных интервалах 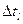и 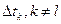, отсутствует. Поэтому корреляционная функция данного процесса равна

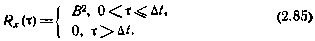
При 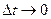отношение 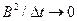. Следовательно, при достаточна малой величине интервала 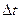процесс x(t) с корреляционной функ­цией R_x(t), определяемой соотношением (2.85), можно рассматри­вать в качестве приближенной аппроксимации белого шума 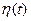с интенсивностью 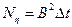. Точность аппроксимации оказывается тем выше, чем меньше интервал .

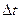При численном интегрировании стохастических дифференци­альных уравнений (2.82) на ЦВМ величина интервала 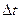, исполь­зуемого при моделировании белого шума 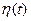, действующего на систему, не может быть задана меньше шага интегрирования 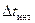. Следовательно, шаг численного интегрирования должен опре­деляться из условия

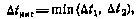
где 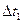— интервал, при котором ступенчатый абсолютно случайный процесс достаточно точно аппроксимирует белый шум; 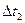— шаг численного интегрирования, обеспечивающий приемлемую точность вычислений при избранном методе численного интегрирования си­стемы (2.82).

Эксперименты на ЦВМ показывают, что при всех методах чис­ленного интегрирования 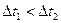, поэтому для обеспечения аппрок­симации белого шума ступенчатым процессом интегрирование си­стемы (2.82) должно вестись с шагом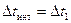

Среди всех методов численного интегрирования затраты машин­ного времени на один шаг интегрирования являются наименьшими при интегрировании по методу Эйлера:

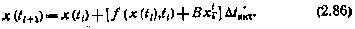
Вследствие этого данный метод и следует использовать при ста­тистическом моделировании систем, беря 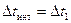, а коэффициент В рассчитывать по формуле

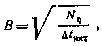
где 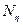— интенсивность белого шума, действующего на систему.

Проведение статистического моделирования и обработка его ре­зультатов. Составив программу моделирования исследуемой дина­мической системы на ЦВМ или набрав схему моделирования на АВМ, с их помощью получают необходимое число реализаций вы