Предел переменной величины. Предел последовательности.

Из разнообразных способов поведения переменных величин наиболее важен тот, при котором переменная величина стремится к некоторому пределу. В этом случае значения, принимаемые переменной величиной х, становятся сколь угодно близкими к некоторому постоянному числу a - пределу этой переменной величины. Говорят, что переменная величина стремится, неограниченно приближается к постоянному числу а (своему пределу). Дадим более подробно соответствующее определение.

Переменная величина х стремится к пределу a (a - постоянное число), если абсолютная величина 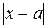разности между х и а становится в процессе изменения переменной величины сколь угодно малой..

То же самое определение можно сказать и другими словами.

Определение.Постоянное число а называется пределом переменной величиных , если 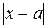- абсолютная величина разности между х и а становится в процессе изменения переменной величины х сколь угодно малой.

Тот факт, что число а, является пределом переменной величины, записывается следующим образом:

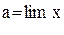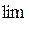( - первые буквы слова limes - предел) или х —> a

Уточним, что следует понимать под словами "величина 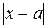становится сколь угодно малой", имеющимися вопределении предела. Зададимся произвольным положительным числом 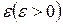, тогда, если, начиная с некоторого момента в изменении переменной величины х, значения 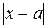сделаются, и будут становиться меньше, чем это .

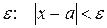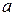Переменная величина стремится к пределу , если для любого положительного 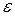. начиная с некоторого момента в изменении переменной , выполняется неравенство .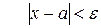

Определение предела имеет простой геометрический смысл: неравенство 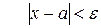означает, что находится в 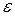-окрестности точки 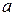, т.е. в интервале 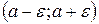(рис. 26). Таким образом, определение предела в геометрической форме: число 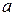является пределом переменной величины , если для любой (произвольно малой) 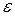-окрестности точки 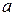можно указать такой момент в изменении переменной начиная с которого все ее значения
попадают в указанную 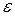-окрестность точки a.

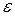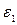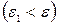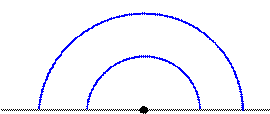
Необходимо представлять себе процесс приближения к пределу в динамике. Взяли некоторую - окрестность точки a; начиная с некоторого момента в изменении , все значения попадают в эту окрестность. Теперь возьмем более тесную - окрестность точки a ; начиная с некоторого (более отдаленного в сравнении с первым) момента в изменении , все ее значения попадут в 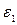- окрестность точки а и т.д. (рис. 1).

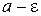
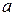
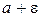
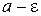
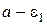
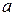
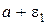
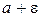
рис. 1

Введя определение предела переменной величины, мы постарались его подробно обсудить и расшифровать. Однако в этом определении осталась нераскрытой одна, весьма существенная, деталь; что следует понимать под словами "начиная с некоторого момента в изменении переменной величины "? Это ясно тогда, когда процесс изменения переменной протекает во времени: начиная с некоторого момента (времени). Но не всегда мы имеем дело с переменными величинами, изменение которых протекает во времени. Как же быть в этих случаях? Выход состоит в расшифровке этого места в общем определении предела переменной специфическим образом для каждого типа переменных величин: по-своему для последовательностей, по-своему для функций и т.д.

Предел последовательности.Прежде всего необходимо вспомнить определение последовательности: если все значения, принимаемые переменной величиной х, можно занумеровать помощью всевозможных натуральных чисел х_},х₂,...х_п,..., причем значение с большим номером принимается после значения с меньшим номером, то говорят, что переменная х пробегает последовательность значений х_х,х₂,...х_п ...; или просто, что имеется последовательность (числовая последовательность).

Определение. Числовой последовательностью называется действительная функция натурального аргумента, т. е. функция, у которой 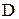=N и ЕÌR.

Она обозначается символом 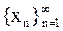, где 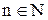, или короче, 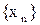. Число 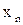, зависящее от n, называется n –ым членом последовательности. Расставив значения последовательности по порядку номеров, получаем, что последовательность можно отождествить со счётным набором действительных чисел, т. е.

.

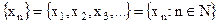Примеры:

а) Последовательность 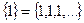является постоянной и состоит из равных чисел (единиц): ;

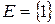б) 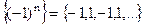. Для неё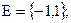

в)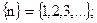

г) .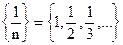

Для последовательностей содержащееся в общем определении предела переменной высказывание "начиная с некоторого момента в изменении " должно означать - "начиная с некоторого номера", так как члены с большими номерами следуют (по определению последовательности) за членом с меньшим номером. Итак, мы получаем следующее определение предела последовательности:

Определение. Число а называется пределом последовательности 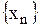, если для любого числа 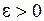найдётся число 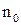, что все числа 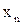, у которых 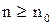, удовлетворяют неравенству .

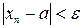Соответствующее обозначение

.

.

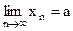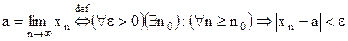Неравенство 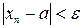можно также записывать в виде 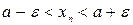или 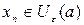. В этих записях подчеркнуто, что величина х_п становится сколь угодно мало отличимой от a , когда номер члена 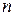неограниченно возрастает. Геометрически определение предела последовательности означает следующее: для сколь угодно малой 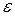-окрестности числа анайдется такой номер N, что все члены последовательности с большими, чем N, номерами попадают в эту окрестность, вне окрестности оказывается лишь конечное число начальных членов последовательности (рис. 2). Это все или некоторые из членов .

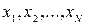x₁ x₂ 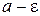x_N+1 a x_N+2 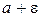x_N x₃

Рис. 2

Число 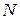в нашем определении зависит от 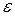: N = N( 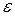) . Как говорилось ранее, определение предела следует понимать в развитии, вдинамике, в движении: если мы возьмем другое, меньшее значение для 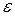, например 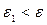то найдется, вообще говоря, другой номер N_x > N, такой, что неравенство 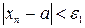, выполняется при всех .

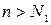Будем записывать определение предела с помощью логических символов (кванторов). Определение предела последовательности с помощью кванторов выглядит так:

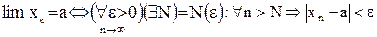
В рассмотренных выше примерах предел имеют последовательности а) и г), а последовательности б) и в) пределов не имеют.

Пример.Доказать, что .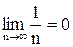

Зададим произвольное 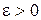. В соответствии с определением мы должны найти такое числ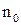о , что 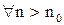выполняется неравенство .

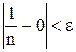Решим это неравенство относительно 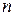. Получим 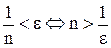. В качестве 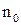берем любое целое 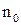больше .

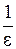Итак, для произвольного 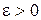найдено числ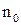о , что 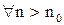выполняется неравенство

.

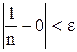Рис. 3

Это и означает по определению, что (Рис. 3) .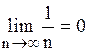

Предел функции