Экспериментальная установка. Определение коэффициента вязкости воздуха и кинематических характеристик теплового движения его молекул: Методические указания к лабораторной работе №23 по

Составитель В. С. Осипов

УДК 536.23 : 531.1

Определение коэффициента вязкости воздуха и кинематических характеристик теплового движения его молекул: Методические указания к лабораторной работе №23 по курсу общей физики/ Уфимск. гос. авиац. техн. ун-т;

Сост. В.С. Осипов. – Уфа, 2001. - 13 с.

В работе на основе исследования одного из явления переноса (внутреннего трения) определяютcя коэффициент вязкости воздуха, а также средняя длина свободного пробега и эффективный диаметр его молекул.

Приведены краткая теория метода, описание экспериментальной установки, указан порядок выполнения работы и форма представления результатов.

Предназначены для студентов, изучающих общий курс физики.

Таабл. 1. Ил. 3. Библиогр.: 2 назв.

Рецензенты: А.Р. Бигаева;

Г.Г. Еникеев.

СОДЕРЖАНИЕ

1. Цель работы 4

2. Теоретическая часть 4

3. Экспериментальная установка 10

4. Порядок выполнения работы 12

5. Требования к отчету 13

6. Контрольные вопросы 13

Список литературы 14

ЛАБОРАТОРНАЯ РАБОТА № 23

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ВОЗДУХА

И КИНЕМАТИЧЕСКИХ ХАРАКТЕРИСТИК

ТЕПЛОВОГО ДВИЖЕНИЯ ЕГО МОЛЕКУЛ

Цель работы

1.1Изучение явления внутреннего трения в газах и измерение коэффициента вязкости воздуха.

1.2 Определение средней длины свободного пробега и эффектив­ного диаметра молекул воздуха.

Теоретическая часть

2.1Кинематические характеристики теплового движения молекул в газах

Молекулы газа, непрерывно и хаотично двигаясь, при взаимодей­ствии между собой изменяют направление своего движения, в резуль­тате чего их траектории представляют собой разупорядоченные лома­ные линии. Процесс взаимодействия молекул, при котором они изменя­ют направление своего движения, называют столкновением, а наимень­шее расстояние, на которое при этом сближаются центры молекул - эффективным диаметром молекулы. Среднее расстояние, проходимое молекулой между двумя последовательными столкновениями, называется средней длиной свободного пробега молекулы. Считая газ идеальным, проследим за движением какой-либо молекулы. В идеальном газе молекулы взаимодействуют только при непосредственном соударении, причем аб­солютно упруго. Поэтому выбранная молекула, столкнувшись с одной, будет двигаться прямолинейно, пока не столкнется с другой молекулой. Это произойдет тогда, когда центр встреченной молекулы окажется расположенным от траек­тории налетающей на нее на расстоянии не большем, чем ее эффек­тивный диаметр. В результате столкновения молекула изменит направление своего движения и некоторое время будет двигаться прямолинейно, пока на ее пути не окажется еще одна молекула, центр которой будет находиться в пределах цилиндра с радиусом основания, равным эффективному диаметру молекул. При средней скорости движения молекулы <V₀> относительно других молекул за время t она проходит путь <V₀>t. Число испытанных ею за это время столкновений

равно количеству молекул, центры которых в соответствии с рисунком 2.1 попадают внутрь ломаного цилиндра длиной <V₀>t

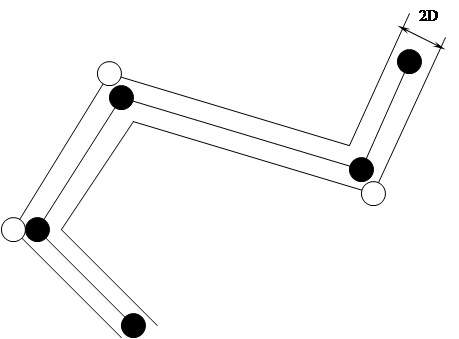Рисунок 2.1

с площадью основания, равной

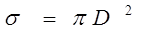, (2.1)

где D - эффективный диаметр молекулы. Эту площадь называют эф­фективным сечением молекул или сечением столкновений. Умножив ко­нцентрацию молекул газа (n) на объем указанного цилиндра, полу­чим среднее число столкновений за время t:

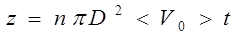. (2.2)

Скорость выбранной нами молекулы относительно тех, с которыми она сталкивается при движении, равна

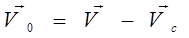, (2.3)

где V скорость выбранной молекулы относительно неподвижной системы отсчета , а V_c - скорость сталкивающейся с ней молекулы относительно той же системы отсчета. Относительная сренеквадратичная скорость равна

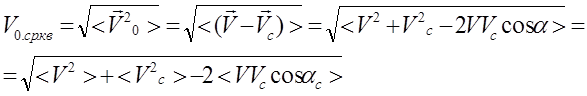.(2.4)

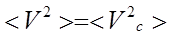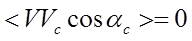Вследствие хаотичности теплового движения молекул и , (2.5)

поэтому 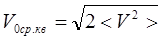, а так как средняя скорость <V> пропорциональна среднеквадратичной, то 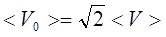и средняя длина свободного пробега оказывается равной

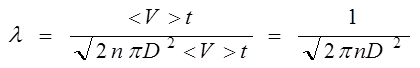.(2.6)

В идеальном газе,концентрация молекул составляет:

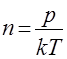,(2.7)

где P - давление газа, T - его абсолютная температура, k= 1,38∙10²³ Дж/К - постоянная Больцмана

Из (2.6) и (2.7) следует уравнение, связывающее эффективный диаметр молекул со средней длиной их свободного пробега через ма­кроскопические параметры, задающие состояние газа:

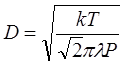. (2.8)

2.2 Взаимосвязь характеристик теплового движения молекул в газах и их определение с помощью измерения параметров течения газа через капилляр.

Всем газам и жидкостям присуще свойство оказывать сопротивление перемещению частей газа или жидкости относительно друг друга. Это их свойство называют внутренним трением или вязкостью. При перемещении слоев газа или жидкости, движущихся параллельно друг другу с различными скоростями, возникают силы, направленные по касательной к поверхности соприкосновения слоев, называемые силами внутреннего трения. При этом со стороны слоя, движущегося быстрее, на соседний слой, который движется медленнее, действует ускоряющая его сила, а со стороны слоя, движущегося медленнее, на слой движущийся с большей скоростью – тормозящая. В итоге скорость движения слоев друг относительно друга уменьшается.

Существование внутреннего трения (или вязкости) в газах обусловлено тем, что упорядоченное движение слоев газа накладывается на беспорядочное тепловое движение молекул, благодаря которому молекулы переходят из одного слоя в другой, перенося при этом свой импульс направленного упорядоченного движения. А в результате столкновений прибывших в данный слой молекул с находящимися там, суммарный импульс упорядоченного движения всех молекул в слое стремится выровняться, т.е. скорость направленного движения соседних слоев друг относительно друга становиться меньше.

Рассмотрим явление вязкости в газе с позиций молекулярно – кинетической теории идеального газа. Величина импульса, переносимого за время Dt через площадку S, расположенную вдоль направления течения газа, слои которого движутся с различными скоростями 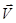(рис 2.2), равна модулю разности импульсов переносимых молекулами, пересекающими эту площадку с разных сторон.

Переносимый молекулами импульс равен произведению импульса отдельной молекулы на число молекул, пересекающих площадку за время Dt. При одинаковом распределении скоростей теплового движения молекул по трем взаимно перпендикулярным напра­влениям можно считать, что из всех n молекул в единице объема газа в среднем только третья часть движется вдоль любой координатной оси, причем лишь половина этой трети - в направлении этой оси. Скорость упорядоченного движения молекул как правило значительно меньше скорости их теплового движения, поэтому среднее число молекул, пересекающих площадку площадью S за время Dt как с одной стороны, так и с другой, одинаковы и равны

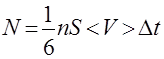. (2.9)

При этом каждой молекулой переносится тот импульс, которым она обладала после последнего столкновения перед площадкой, то есть находясь от площадки на расстоянии порядка средней длины свобод­ного пробега λ . Если в соответствии с рисунком 2.2 скорость течения газа, расположенного слева на этом расстоянии от площад­ки S, равна 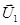, а справа - 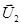, то при массе молекулы m суммарный импульс упорядоченного движения, пе­реносимый за время Dt через площадку слева направо, равен

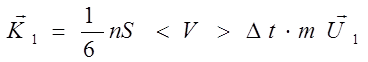, (2.10)

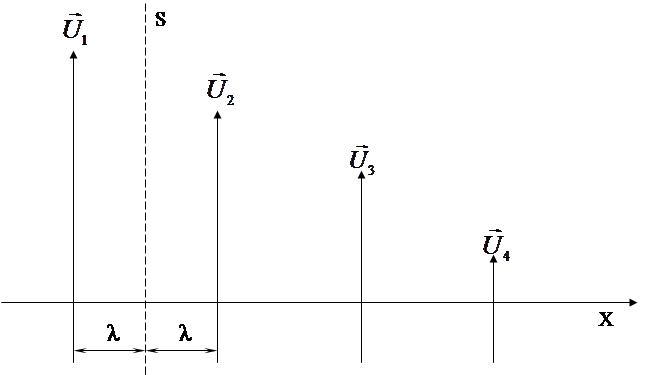
Рисунок 2.2

а справа налево

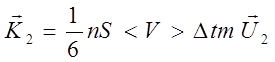. (2.11)

В итоге за время Δt через площадь S в направлении уменьшения скорости переносится импульс величиной

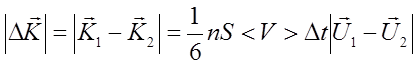. (2.12)

Модуль разности скоростей течения 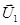и 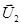можно представить в виде:

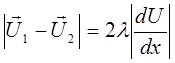, (2.13)

где 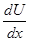- проекция вектора градиента модуля скорости упорядоченно­го движения на ось X . Подстановка (2.13) в (2.12) дает

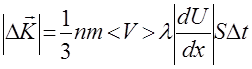. (2.14)

Экспериментально же установлено, что сила внутреннего трения, возникающая между двумя соседними слоями газа с площадью соприкосновения S, движущимися параллельно с различными скоростями, при не очень больших скоростях прямо пропорциональна площади S и модулю проекции вектора градиента абсолютной величины скорости направленного движения слоев на перпендикулярную этой скорости ось x:

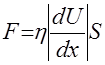. (2.15)

Вектор градиента модуля скорости упорядоченного движения направлен в сторону наибольшего ее возрастания и показывает как сильно изменяется скорость вдоль оси x по мере перехода от одного слоя к другому. Коэффициент η в формуле (2.15), зависящий от природы газа и условий, в которых он находится, называют динамической вязкостью (часто просто вязкостью) или коэффициентом вязкости. В системе СИ он измеряется в Па·с, а его физический смысл заключается в том, что численно он равен силе внутреннего трения, приходящейся на единицу площади соприкасающихся движущихся слоев газа при единичном значении проекции градиента модуля скорости их направленного движения.

Следуя второму закону Ньютона:

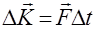, (2.16)

из (2.14) и (2.15) получаем уравнение, связывающее среднюю скорость свободного пробега молекул в газе с его динамической вязкостью.

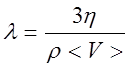, (2.17)

где ρ – плотность газа.

Один из наиболее простых способов определения коэффициента вязкости газа заключается в измерении разности давлений газа на концах достаточно узкой (капиллярной) трубки при протекании через нее газа.

В капиллярной трубке течение газа ламинарное, поэтому его объем, проходящий через трубку за время t , определяется по формуле Пуазейля.

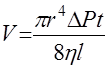, (2.18)

где ΔP - разность давлений газа на концах трубки, обуславливаю­щая его течение в ней, а r и l - радиус и длина трубки. Таким образом, при известных геометрических размерах капилляра достаточно знать объемную скорость прохождения газа через трубку и разность давлений на ее концах, чтобы вычислить коэффициент вязкости.

Согласно (2.18),

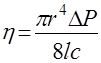, (2.19)

где С - объемная скорость истечения газа.

Зная коэффициент вязкости газа, через термодинамические пара­метры его состояния нетрудно рассчитать среднюю длину свободного пробега молекул и их эффективный диаметр. Из молекулярно-кинетической теории следует, что средняя скорость теплового движения молекул в газе равна

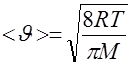, (2.20)

где R = 8,31 Дж/моль k - газовая постоянная, M - молярная масса газа.

Выразив из уравнения состояния плотность газа

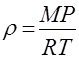(2.21)

и подставив (2.20) и (2.21) в (2.17) получим

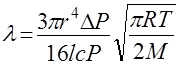. (2.22)

Используя это выражение для λ, из (2.6) можно найти D:

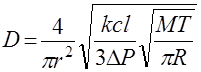(2.23)

Экспериментальная установка

Установка изображена на рисунке 3.1. Она состоит из перистальтического насоса 1 типа PP-I-05, герметичного резервуара 2, со­общающегося с атмосферой через капиллярную трубку 3, и водяного манометра 4 со шкалой 5. Одно из колен манометра сообщается с ат­мосферой, а другое - с резервуаром.

При включении насоса воздух из резервуара будет откачиваться через соединительную трубку 6. Несмотря на то, что резервуар сооб­щается с атмосферой, давление воздуха в нем начнет уменьшаться, так как за некоторый начальный промежуток времени объем откачива­емого из резервуара воздуха будет больше объема воздуха, поступа­ющего в него через капиллярную трубку.

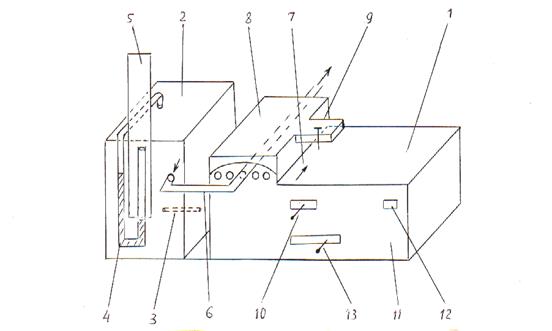
Рисунок 3.1

По мере понижения давления в резервуаре разность давлений на концах капиллярной трубки растет, что приводит к увеличению объема воздуха, поступающего через нее в резервуар за единицу времени. При неизменной производительности насоса увеличение этого объема будет происходить до тех пор, пока он не станет равным объему воздуха, удаляемого насосом за ту же единицу времени. С этого момента разность давлений на концах капи­ллярной трубки будет оставаться одной и той же. Ее величина, рав­ная разности между атмосферным давлением и давлением воздуха в ре­зервуаре, зависит от производительности насоса и находится по разности высот уровней воды в коленах манометра

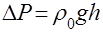, (3.1)

где ρ₀ плотность воды, g - ускорение свободного падения, h - разность высот уровней. С учетом (3.1) уравнения (2.19), (2.22) и (2.23) можно представить в виде

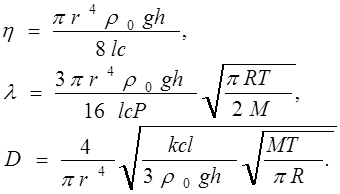(3.2)

Порядок выполнения работы

4.1 Убедившись в том, что трубка 6, через которую откачивает­ся воздух из резервуара, находится в среднем канале насоса откры­тым концом в направлении стрелки 7 на верхней панели насоса, нак­ройте ее зажимной крышкой 8. Прижмите крышку ручкой 9, расположив ее так, чтобы стрелка на ней была направлена вдоль стрелки 7. При необходимости той же ручкой 9 отрегулируйте нажим так, чтобы произошло перекрытие трубки 6 в верхней части, не допуская при этом излишних усилий.

4.2Установите переключатель 10 управления множительным меха­низмом скоростей откачки в положение "х10". Установка переключателя производится нажатием его вниз с последующим перемещением в ну­жную сторону и фиксацией отжатием вверх. Таким же образом устано­вите переключатель скоростей откачки 13 в крайнее левое положение.

4.3 Подсоедините насос к сети и включите его выключателем II. При этом должна загореться сигнальная лампочка 12.

4.4 Установите переключатель скоростей 13 в положение под наименьшим номером из трех, какие укажет преподаватель, и наб­людайте за изменением высот столбов воды в манометре до тех пор, пока оно через несколько минут не остановится. Измерьте установив­шуюся разность высот уровней воды в коленах манометра по шкале 5.

4.5Устанавливая последовательно переключатель 13 в другие два положения в порядке возрастания их номеров, измерьте устано­вившуюся разность высот уровней для этих положений.

4.6 По барометру и термометру в лаборатории определите давле­ние и абсолютную температуру атмосферного воздуха.

4.7 В прилагаемом к установке паспорте найдите значения ско­ростей откачки, соответствующие тем положениям переключателя, при которых проводились измерения, а также геометрические размеры трубки. Используя эти данные, для каждой из трех экспериментально полученных разностей высот уровней воды по формулам (3.2) вычисли­те коэффициент вязкости воздуха, среднюю длину свободного пробега его молекул и их эффективный диаметр. При вычислениях считать M = 0,029 кг/моль, ρ₀=10³ 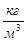, g=9,8 .

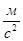4.8 Рассчитайте относительные систематические ошибки опреде­ления η, λ и D .

Требования к отчету

Результаты измерений и расчетов представляются в виде табли­цы с приведенными под ней значениями радиуса и длины капилляра, давления и температуры.

Таблица

_________________________________________________________

С , 10^-8 м³/с

h , мм

η , 10^-5 Па с

λ , нм

D , нм

η_ср, 10^-5 Па с

λ_ср, нм

D_ср, нм

δη, %

δλ, %

δD, %

_______________________________________________________

Контрольные вопросы

1.Какое физическое явление изучается в данной работе?

2.Что такое коэффициент вязкости? В каких единицах он измеряется? Каков его смысл?

3.Что такое средняя длина свободного пробега молекул? Как она зависит от давления и температуры газа?

4.Что называют эффективным диаметром молекулы?

5.Какой порядок величины средней длины свободного пробега и эффективного диаметра молекул газов при условиях, не сильно отли­чающихся от нормальных?

6.В чем заключается принцип работы экспериментальной установки, используемой в работе?

7.Чем определяется сила внутреннего трения в газах?

Список литературы

1. Савельев И.В. Курс общей физики. Т. I. - М.: Наука, 1989. - С. 269-274, 285-287.

2. Матвеев А.Н. Молекулярная физика. - М.: Высшая школа, 1987. - С. 10-12, 14-16, 66-70, 321-324.