Формула полной вероятности, асимптотические формулы

51. В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.

52. Имеется две партии изделий по 12 и 10 штук, причем в первой партии одно изделие бракованное, а во второй партии два изделия бракованные. Изделие, взятое наудачу из первой партии, переложено во вторую, после чего выбирается наудачу изделие из второй партии. Определить вероятность извлечения бракованного изделия из второй партии.

53. Три станка автомата выпускают однотипные детали одного и того же количества. Вероятность появления бракованной детали для каждого станка равна 0,1, 0,05, 0,07 соответственно. Все детали произведенные станками помещаются в один ящик. Из него наудачу выбирают деталь, какова вероятность взятия стандартной детали.

54. Что вероятнее выиграть у равносильного противника: 1) три партии из четырех или пять из восьми? 2) не менее трех партий из четырех или не менее пяти партий из восьми?

55. Имеется 5 станций, с которыми поддерживается связь. Время от времени связь прерывается из-за атмосферных помех. Вследствие удаленности станций друг от друга перерыв связи с каждой из них происходит независимо от остальных с вероятностью 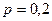. Найти вероятность того, что в данный момент времени будет иметься связь не более чем с двумя станциями.

56. Прибор состоит из 8 однородных элементов, но может работать при наличии в исправном состоянии не менее 6 из них. Каждый из элементов за время работы прибора 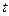выходит из строя независимо от других с вероятностью 0,2. Найти вероятность того, что прибор откажет за время .

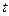57. При технологическом процессе 85% всей произведенной продукции высшего сорта. Найти наивероятнейшее число изделий высшего сорта в партии из 150 изделий.

58. Вероятность получения с конвейера изделий 1 сорта равна 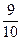. Определить вероятность того, что из взятых на проверку 600 изделий 530 будут 1 сорта. Определить наивероятнейшее число изделий первого сорта.

59. Вероятность того, что деталь не прошла проверку отдела технического контроля 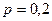. Найти вероятность того, что среди 400 случайным образом отобранных деталей окажется непроверенных от 70 до 100 деталей.

60. Вероятность производства стандартной детали равна 0,75. Найти вероятность того, что из 100 деталей стандартных будет: а) не менее 70 и не более 80 раз; б) не более 70 раз.

Случайные величины

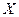	-2
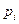	0,1	0,3	0,4	0,2

61. Дискретная случайная величина задана рядом распределения. Построить многоугольник распределения, функцию распределения и ее график.

62. В магазин в течении часа заходят 3 покупателя. Каждый из них совершает одну покупку с вероят­ностью 0,6;0,7;0,8 соответственно. Составить ряд распределения случайной величины выра­жающей число покупок. Построить полигон этой случайной величины, функцию распределения этой величины и ее график.

63. В лотерее из 50 билетов 4 выигрышных по 25, 50, 60 и 70 рублей. Некто покупает 4 билета. Составить ряд распределения случайной величины выражающей сумму выигрыша. Построить многоугольник распределения, функцию распределения, график функции распределения.

64. Задана непрерывная случайная величина своей функцией распределения 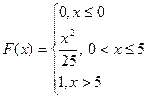. Найти плотность распределения случайной величины.

65. Непрерывная случайная величина задана плотностью распределения 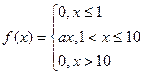. Найти параметр 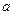, интегральную функцию распределения.

66. Случайная величина 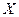задана интегральной функцией 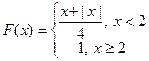. Найти дифференциальную функцию .

67. Задана плотность распределения случайной величины х: Найти: функцию распределения F(x); .

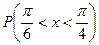68. Случайная величина задана функцией распределения 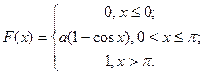Найти , .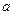

69. Функция распределения случайной величины x задана выражением: 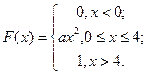Найти коэффициент 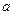, плотность вероятности и .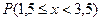

70. Функция распределения случайной величины x задана выражением: 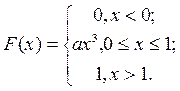Найти коэффициент 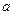, плотность вероятности и 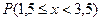.