Несобственные интегралы I-го рода

Пусть функция f(x) определена и непрерывна на промежутке [a, ¥). Тогда она непрерывна на любом отрезке [a, b].

Если существует конечный предел 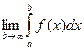, то этот предел называется несобственным интегралом1-го рода от функции f(x) на промежутке [a, ¥).

Обозначается: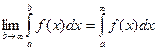

Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.

Если предел не существует или бесконечен, то несобственный интеграл расходится.

Геометрический смысл несобственного интеграла I рода заключается в следующем: если 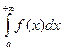сходится (при условии, что f(x)≥0), то он представляет собой площадь "бесконечно длинной" криволинейной трапеции (рис. 24.1).

Аналогично вводится понятие несобственного интеграла с бесконечным нижним пределом интегрирования для непрерывной на промежутке (-∞;b] функции: = .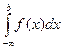

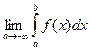Несобственный интеграл с двумя бесконечными пределами интегрирования определяется формулой: 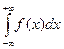= 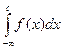+ 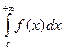, где с – произвольное число.

Рассмотрим примеры нахождения несобственных интегралов I рода.

Несобственные интегралы II-го рода.

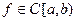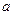Пусть , где и 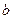– некоторые числа, причем 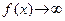при 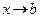(функция неограничена). Тогда .

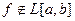Возьмем 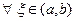. Тогда 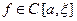и, следовательно, .

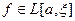Несобственным интегралом 2-го рода функции 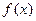на промежутке 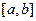называют предел .

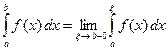Если этот предел существует и конечен, то несобственный интеграл называют сходящимся, в противном случае – расходящимся.

Так же, как и выше, определяют интеграл от функции, неограниченной в окрестности точки .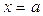

Геометрический смысл несобственного интегралаII рода 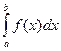, где b – точка разрыва второго рода, f(x)≥0, заключается в следующем: если 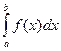сходится, то он представляет собой площадь "бесконечно высокой" криволинейной трапеции (рис. 24.2).

Аналогично вводится понятие несобственного интеграла II рода для непрерывной на промежутке (a;b]функции при условии, что а – точка разрыва второго рода: = .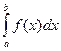

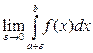Дифференциальные уравнения. Основные понятия.

Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию у=f(x) и её производные 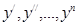. Общий вид дифференциального уравнения:

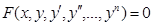или

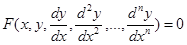
Порядок дифференциального уравненияопределяется порядком наивысшей производной, входящей в данное уравнение:

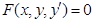-дифференциальное уравнение первого порядка.

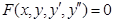-дифференциальное уравнение второго порядка.

Дифференциальное уравнение называется полным, если оно содержит в себе свободный член, производные, начиная с производной нулевого порядка, затем производных первого, второго и всех последующих порядков. Если же один из этих членов отсутствует, то уравнение называется неполным.

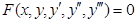-полное дифференциальное уравнение

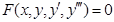-неполное дифференциальное уравнение

Дифференциальное уравнение называется приведённым, если в его правой части стоит ноль.

Дифференциальное уравнение называется обыкновенным, если искомая функция 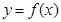есть функция одного аргумента.

Решением или интеграломдифференциального уравнения называется всякая функция 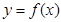, которая будучи подставлена в дифференциальное уравнение (вместе со своими производными), превращает его в тождество.

Всякое решение, которое содержит столько произвольных постоянных, каков порядок уравнения, называется общим решением. Решение, полученное из общего решения, путём задания произвольным постоянным определённых численных значений, называется частным решением. На практике частное решение получается из общего решения не прямым заданием значений произвольных постоянных, а исходя из тех условий, которым должно удовлетворять искомое частное решение.

Основные понятия и определения дифференциальных уравнений

Дифференциальным уравнением называется уравнение, связывающее независимую переменную 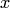, искомую функцию 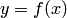и её производные 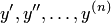, т. е. уравнение вида

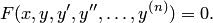
Если искомая функция 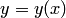есть функция одной независимой переменной 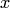, дифференциальное уравнение называется обыкновенным; например,

Когда искомая функция 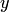есть функция двух и более независимых переменных, например, если 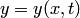, то уравнение вида называется уравнением в частных производных. Здесь 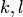— неотрицательные целые числа, такие, что 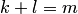; например

Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например, дифференциальное уравнение 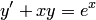— уравнение первого порядка, дифференциальное уравнени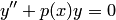е , где 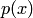— известная функция, — уравнение второго порядка; дифференциальное уравнение 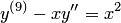— уравнение 9-го порядка.

Решением дифференциального уравнения n-го порядка на интервале 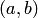называется функция 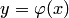, определенная на интервале 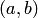вместе со своими производными до n-го порядка включительно, и такая, что подстановка функции 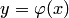в дифференциальное уравнение превращает последнее в тождество по 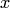на 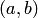. Например, функция 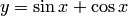является решением уравнения 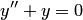на интервале 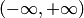. В самом деле, дифференцируя функцию дважды, будем иметь

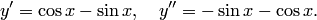
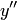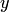Подставляя выражения и в дифференциальное уравнение, получим тождество

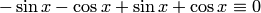
График решения дифференциального уравнения называется интегральной кривой этого уравнения.

Общий вид уравнения первого порядка

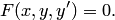
(1)

Если уравнение (1) удается разрешить относительно 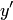, то получится уравнение первого порядка, разрешенное относительно производной.

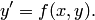
(2)

Задачей Коши называют задачу нахождения решения 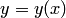уравнения 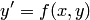, удовлетворяющего начальному условию 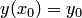(другая запись ).

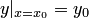Геометрически это означает, что ищется интегральная кривая, проходящая через заданную
точку 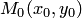плоскости 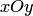(рис. 1).

Теорема существования и единственности решения задачи Коши

Пусть дано дифференциальное уравнение 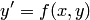, где функция 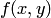определена в некоторой области 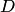плоскости 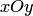, содержащей точку 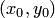. Если функция 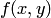удовлетворяет условиям

а) 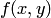есть непрерывная функция двух переменных 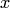и 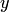в области 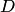; б) 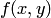имеет частную производную 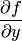, ограниченную в области 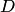, то найдется интервал 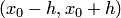, на котором существует единственное решение 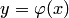данного уравнения, удовлетворяющее условию .

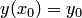Теорема дает достаточные условия существования единственного решения задачи Коши для уравнения 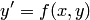, но эти условия не являютсянеобходимыми. Именно, может существовать единственное решение уравнения 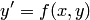, удовлетворяющее условию 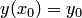, хотя в точке 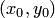не выполняются условия а) или б) или оба вместе.

Условие Липшица

Замечание. Условие ограниченности производной 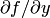, фигурирующее в теореме существования и единственности решения задачи Коши, может быть несколько ослаблено и заменено так называемым условием Липшица.

Говорят, что функция 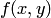, определенная в некоторой области 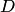, удовлетворяет в 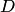условию Липшица по 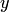, если существует такая постоянная 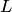(постоянная Липшица), что для любых 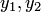из 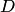и любого 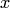из 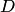справедливо неравенство

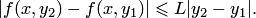
Существование в области 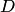ограниченной производной 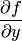достаточно для того, чтобы функция 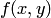удовлетворяла в 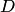условию Липшица. Напротив, из условия Липшица не вытекает условие ограниченности 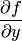; последняя может даже не существовать. Например, для уравнения 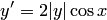функция 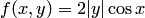не дифференцируема по 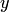в точке 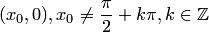, но условие Липшица в окрестности этой точки выполняется. В самом деле,

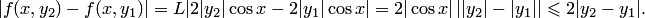
поскольку 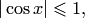а 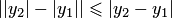. Таким образом, условие Липшица выполняется с постоянной .

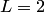Теорема. Если функция 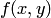непрерывна и удовлетворяет условию Липшица по 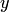в области 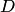, то задача Коши

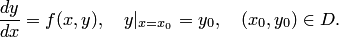
имеет единственное решение.

Условие Липшица является существенным для единственности решения задачи Коши. В качестве примера рассмотрим уравнение

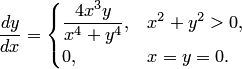
Нетрудно видеть, что функция 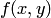непрерывна; с другой стороны,

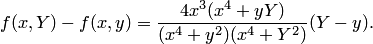
Если 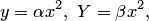то

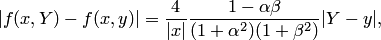
и условие Липшица не удовлетворяется ни в одной области, содержащей начало координат 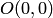, так как множитель при 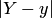оказывается неограниченным при .
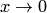Данное дифференциальное уравнение допускает решени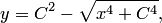е где 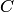— произвольная постоянная. Отсюда видно, что существует бесконечное множество решений, удовлетворяющих начальному условию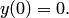

Общим решением дифференциального уравнения (2) называется функция

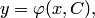
(3)

зависящая от одной произвольной постоянной 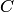, и такая, что
1) она удовлетворяет уравнению (2) при любых допустимых значениях постоянной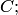

2) каково бы ни было начальное условие

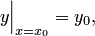
(4)

можно подобрать такое значение 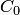постоянной 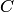, что решение 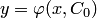будет удовлетворять заданному начальному условию (4). При этом предполагается, что точка 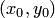принадлежит области, где выполняются условия существования и единственности решения.

Частным решением дифференциального уравнения (2) называется решение, получаемое из общего решения (3) при каком-либо определенном значении произвольной постоянной