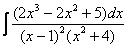Общее правило: ВСЁ, что в знаменателе МОЖНО разложить на множители – раскладываем на множители
Непосредственное интегрирование
Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. См. Таблица интегралов.
Править] Подведение под знак дифференциала
Данный метод эквивалентен методу замены переменной (см. далее):
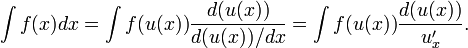
[править] Метод замены переменной (метод подстановки)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 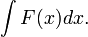 Сделаем подстановку
Сделаем подстановку 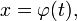 где
где 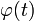 — функция, имеющая непрерывную производную.
— функция, имеющая непрерывную производную.
Тогда 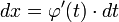 и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
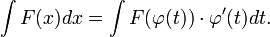
[править] Интегрирование выражений вида 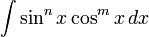
Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
Если n и m чётные, то удобнее сделать подстановку tg x = t.
Править] Примеры
Вычислить: 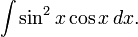
Пусть 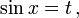 тогда
тогда 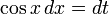 и
и 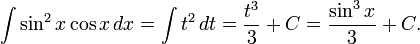
Править] Интегрирование по частям
Основная статья: Интегрирование по частям
Интегрирование по частям — применение следующей формулы для интегрирования:
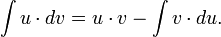
В частности, с помощью n-кратного применения этой формулы находится интеграл
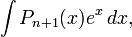
где Pn + 1(x) — многочлен (n + 1)-ой степени.
Править] Интегрирование рациональных дробей
Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.
Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.
Всякую правильную рациональную дробь 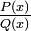 , знаменатель которой разложен на множители
, знаменатель которой разложен на множители
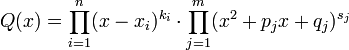
можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:
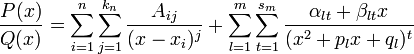
где Aij,αlt,βlt — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.
Править] Примеры
Вычислить: 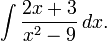
Разложим подынтегральное выражение на простейшие дроби:
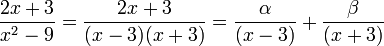
Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями:
α(x + 3) + β(x − 3) = 2x + 3
(α + β)x + 3α − 3β = 2x + 3
Следовательно 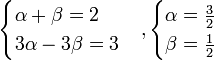
Тогда 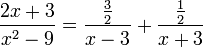
Теперь легко вычислить исходный интеграл 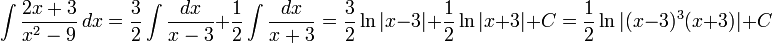
Интегрирование простейших рациональных дробей. Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул: 1. 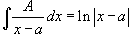 2. 2. 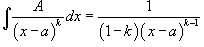 У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат: У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат: 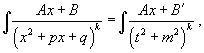 где где 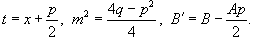 Затем применяются следующие формулы: 3. Затем применяются следующие формулы: 3. 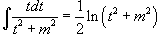 4. 4. 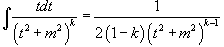 5. 5. 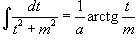 Интеграл Интеграл 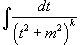 может быть вычислен за k шагов с помощью формулы редукции 6. может быть вычислен за k шагов с помощью формулы редукции 6. 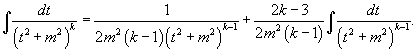 |
| Пример 1 |
Вычислить интеграл 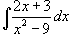 . Решение. Разложим подынтегральное выражение на простейшие дроби: . Решение. Разложим подынтегральное выражение на простейшие дроби: 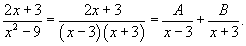 Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями: Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями: 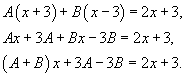 Следовательно, Следовательно, 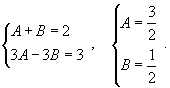 Тогда Тогда 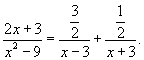 Теперь легко вычислить исходный интеграл Теперь легко вычислить исходный интеграл 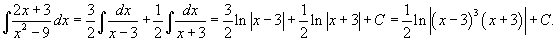 |
| Пример 2 |
Вычислить интеграл 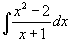 . Решение. Сначала выделим правильную рациональную дробь, разделив числитель на знаменатель. . Решение. Сначала выделим правильную рациональную дробь, разделив числитель на знаменатель. 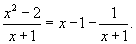 Получаем Получаем 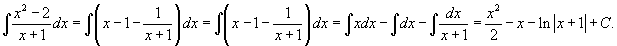 |
| Пример 3 |
Вычислить интеграл 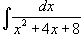 . Решение. . Решение. 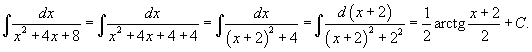 |
| Пример 4 |
Вычислить интеграл 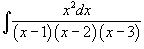 . Решение. Разложим подынтегральное выражение на сумму простейших дробей, используя метод неопределенных коэффициентов: . Решение. Разложим подынтегральное выражение на сумму простейших дробей, используя метод неопределенных коэффициентов: 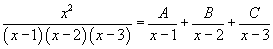 Определим ы: Определим ы: 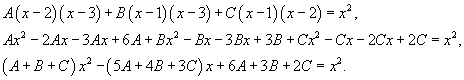 Следовательно, Следовательно, 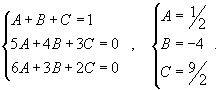 Получаем Получаем 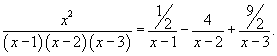 Интеграл, соответственно, равен Интеграл, соответственно, равен 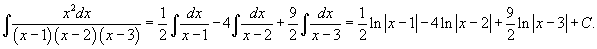 |
| Пример 5 |
Найти интеграл 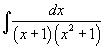 . Решение. Разложим подынтегральное выражение на сумму двух дробей. . Решение. Разложим подынтегральное выражение на сумму двух дробей. 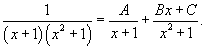 Найдем неизвестные коэффициенты. Найдем неизвестные коэффициенты. 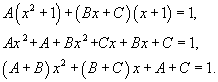 Отсюда получаем Отсюда получаем 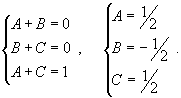 Подынтегральное выражение представляется в виде Подынтегральное выражение представляется в виде 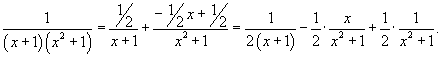 Исходный интеграл равен Исходный интеграл равен 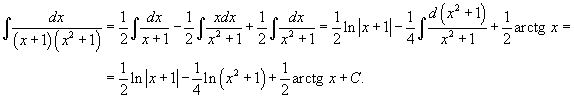 |
| Пример 6 |
Найти интеграл 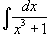 . Решение. Разложим знаменатель в подынтегральном выражении на множители: . Решение. Разложим знаменатель в подынтегральном выражении на множители: 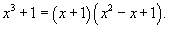 Далее представим подынтегральное выражение в виде суммы простейших дробей Далее представим подынтегральное выражение в виде суммы простейших дробей 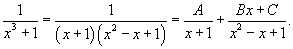 Определим коэффициенты: Определим коэффициенты: 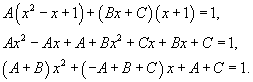 Следовательно, Следовательно, 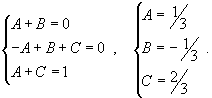 Отсюда находим Отсюда находим 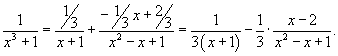 Теперь вычислим исходный интеграл Теперь вычислим исходный интеграл 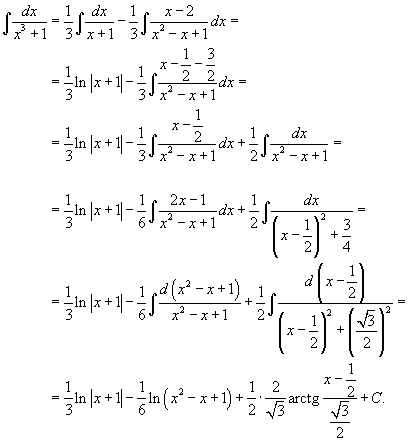 |
| Пример 7 |
Вычислить интеграл 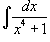 . Решение. Перепишем знаменатель рациональной дроби в следующем виде: . Решение. Перепишем знаменатель рациональной дроби в следующем виде: 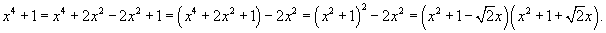 Поскольку полученные множители являются несократимыми квадратичными функциями, то подынтегральное выражение представляется в виде Поскольку полученные множители являются несократимыми квадратичными функциями, то подынтегральное выражение представляется в виде 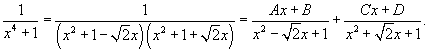 Определим неизвестные коэффициенты. Определим неизвестные коэффициенты. 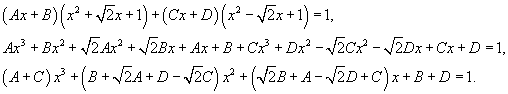 Получаем Получаем 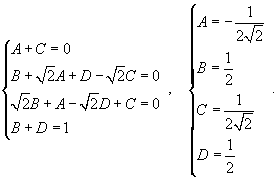 Следовательно, Следовательно, 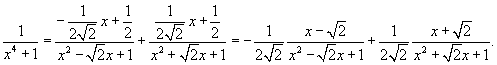 Интегрируем каждое слагаемое и находим ответ. Интегрируем каждое слагаемое и находим ответ. 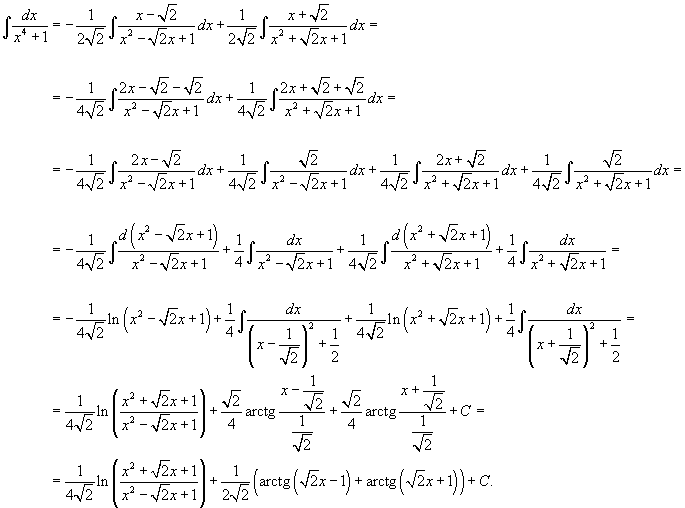 |
| Пример 8 |
Вычислить интеграл 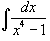 . Решение. Разложим знаменатель на множители: . Решение. Разложим знаменатель на множители: 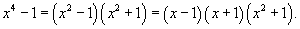 Запишем подынтегральную дробь в виде суммы простейших дробей. Запишем подынтегральную дробь в виде суммы простейших дробей. 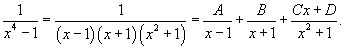 Сгруппируем члены с одинаковыми степенями чтобы определить неизвестные коэффициенты из системы линейных уравнений. Сгруппируем члены с одинаковыми степенями чтобы определить неизвестные коэффициенты из системы линейных уравнений. 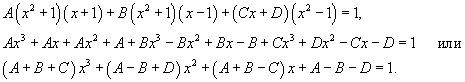 Следовательно, Следовательно, 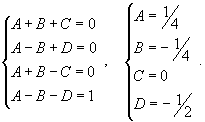 Таким образом, подынтегральное выражение представляется в виде Таким образом, подынтегральное выражение представляется в виде 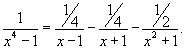 Окончательно находим Окончательно находим 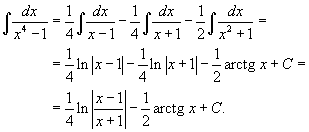 |
| Пример 9 |
Вычислить интеграл 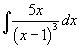 . Решение. Разложим подынтегральное выражение на сумму простейших дробей, учитывая что знаменатель имеет кратный корень 3-го порядка: . Решение. Разложим подынтегральное выражение на сумму простейших дробей, учитывая что знаменатель имеет кратный корень 3-го порядка: 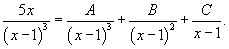 Определим неизвестные коэффициенты. Определим неизвестные коэффициенты. 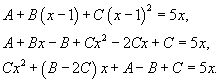 Получаем систему уравнений Получаем систему уравнений 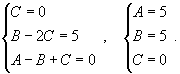 Следовательно, Следовательно, 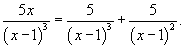 Исходный интеграл равен Исходный интеграл равен 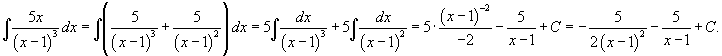 |
| Пример 10 |
Вычислить интеграл 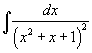 . Решение. Поскольку . Решение. Поскольку 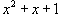 - несократимый квадратный трехчлен, выделим в знаменателе полный квадрат: - несократимый квадратный трехчлен, выделим в знаменателе полный квадрат: 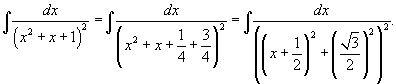 Найдем полученный интеграл с помощью формулы редукции Найдем полученный интеграл с помощью формулы редукции 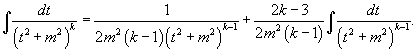 Получаем ответ: Получаем ответ: 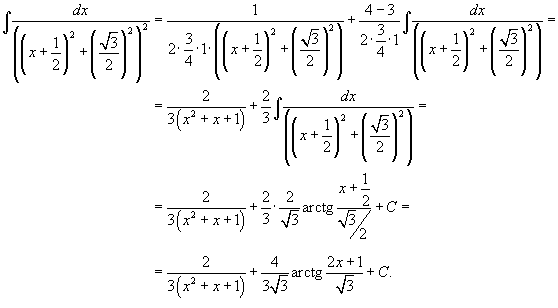 |
Пример.
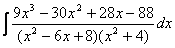
Т.к. ( 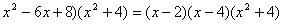 , то
, то
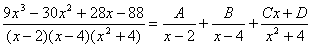
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
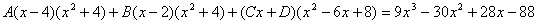
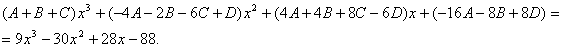
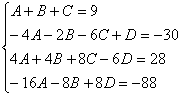
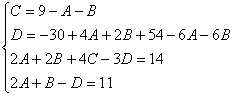
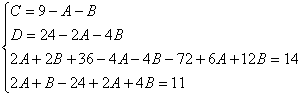
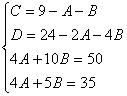
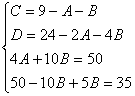
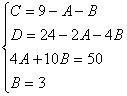
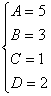
Итого:
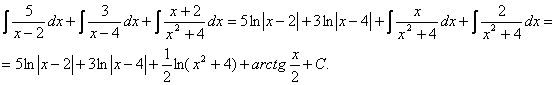
Пример.
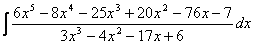
Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:
6x5 – 8x4 – 25x3 + 20x2 – 76x – 7 3x3 – 4x2 – 17x + 6
6x5 – 8x4 – 34x3 + 12x2 2x2 + 3
9x3 + 8x2 – 76x - 7
9x3 – 12x2 – 51x +18
20x2 – 25x – 25
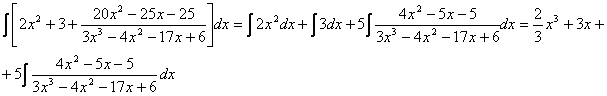
Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:
3x3 – 4x2 – 17x + 6 x - 3
3x3 – 9x2 3x2 + 5x - 2
5x2 – 17x
5x2 – 15x
- 2x + 6
-2x + 6
Таким образом 3x3 – 4x2 – 17x + 6 = (x – 3)(3x2 + 5x – 2) = (x – 3)(x + 2 )(3x – 1). Тогда:
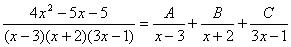
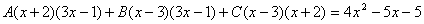
Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:
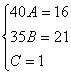
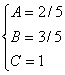
Окончательно получаем:
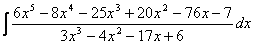 =
= 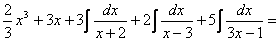
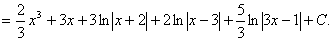
Пример.
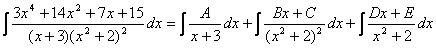
Найдем неопределенные коэффициенты:
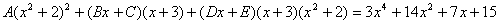
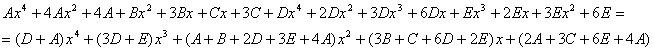
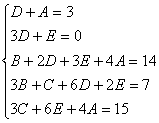
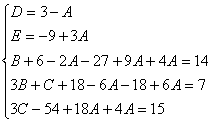
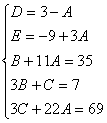
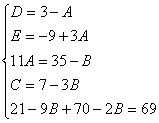
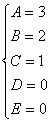
Тогда значение заданного интеграла:
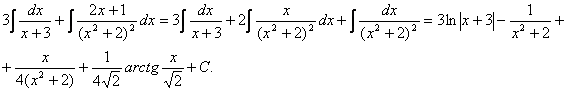
Пример 1
Найти неопределенный интеграл.
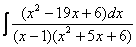
Шаг 1.Первое, что мы ВСЕГДА делаем при решении интеграла от дробно-рациональной функции – это выясняем следующий вопрос: является ли дробь правильной? Данный шаг выполняется устно, и сейчас я объясню как:
Сначала смотрим на числитель и выясняем старшую степень многочлена:
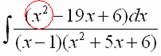
Старшая степень числителя равна двум.
Теперь смотрим на знаменатель и выясняем старшую степень знаменателя. Напрашивающийся путь – это раскрыть скобки и привести подобные слагаемые, но можно поступить проще, в каждой скобке находим старшую степень
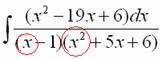
и мысленно умножаем: 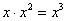 – таким образом, старшая степень знаменателя равна трём. Совершенно очевидно, что если реально раскрыть скобки, то мы не получим степени, больше трёх.
– таким образом, старшая степень знаменателя равна трём. Совершенно очевидно, что если реально раскрыть скобки, то мы не получим степени, больше трёх.
Вывод: Старшая степень числителя СТРОГО меньше старшей степени знаменателя, значит, дробь является правильной.
Если бы в данном примере в числителе находился многочлен 3, 4, 5 и т.д. степени, то дробь была бы неправильной.
Сейчас мы будем рассматривать только правильные дробно-рациональные функции. Случай, когда степень числителя больше либо равна степени знаменателя, разберём в конце урока.
Шаг 2. Разложим знаменатель на множители. Смотрим на наш знаменатель:
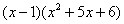
Вообще говоря, здесь уже произведение множителей, но, тем не менее, задаемся вопросом: нельзя ли что-нибудь разложить еще? Объектом пыток, несомненно, выступит квадратный трехчлен. Решаем квадратное уравнение:
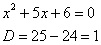
Дискриминант больше нуля, значит, трехчлен действительно раскладывается на множители:
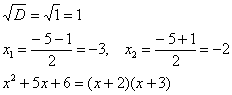
Общее правило: ВСЁ, что в знаменателе МОЖНО разложить на множители – раскладываем на множители.
Начинаем оформлять решение:
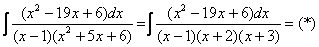
Шаг 3. Методом неопределенных коэффициентов раскладываем подынтегральную функцию в сумму простых (элементарных) дробей. Сейчас будет понятнее.
Смотрим на нашу подынтегральную функцию:
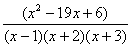
И, знаете, как-то проскакивает интуитивная мысль, что неплохо бы нашу большую дробь превратить в несколько маленьких. Например, вот так:
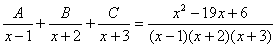
Возникает вопрос, а можно ли вообще так сделать? Вздохнем с облегчением, соответствующая теорема математического анализа утверждает – МОЖНО. Такое разложение существует и единственно.
Только есть одна загвоздочка, коэффициенты 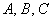 мы пока не знаем, отсюда и название – метод неопределенных коэффициентов.
мы пока не знаем, отсюда и название – метод неопределенных коэффициентов.
Как вы догадались, последующие телодвижения так, не гоготать! будут направлены на то, чтобы как раз их УЗНАТЬ – выяснить, чему же равны 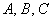 .
.
Будьте внимательны, подробно объясняю один раз!
Итак, начинаем плясать от:
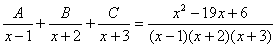
В левой части приводим выражение к общему знаменателю:
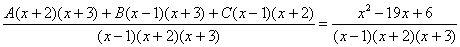
Теперь благополучно избавляемся от знаменателей (т.к. они одинаковы):
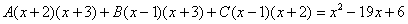
В левой части раскрываем скобки, неизвестные коэффициенты 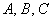 при этом пока не трогаем:
при этом пока не трогаем:
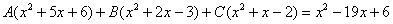
Заодно повторяем школьное правило умножение многочленов. В свою бытность учителем, я научился выговаривать это правило с каменным лицом: Для того чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
С точки зрения понятного объяснения коэффициенты 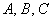 лучше внести в скобки (хотя лично я никогда этого не делаю в целях экономии времени):
лучше внести в скобки (хотя лично я никогда этого не делаю в целях экономии времени):
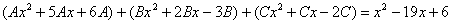
Составляем систему линейных уравнений.
Сначала разыскиваем старшие степени:
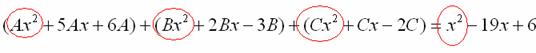
И записываем соответствующие коэффициенты в первое уравнение системы:
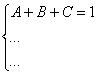
Хорошо запомните следующий нюанс. Что было бы, если б в правой части вообще не было ? Скажем, красовалось бы просто без всякого квадрата? В этом случае в уравнении системы нужно было бы поставить справа ноль: . Почему ноль? А потому-что в правой части всегда можно приписать этот самый квадрат с нулём: . Если в правой части отсутствует какие-нибудь переменные или (и) свободный член, то в правых частях соответствующих уравнений системы ставим нули.
Далее процесс идет по снижающейся траектории, от водки к пиву, отмечаем все «иксы»:
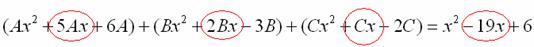
Записываем соответствующие коэффициенты во второе уравнение системы:
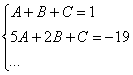
И, наконец, минералка, подбираем свободные члены.
Эх,…что-то я расшутился. Шутки прочь – математика наука серьезная. У нас в институтской группе никто не смеялся, когда доцент на лекции сказала, что разбросает члены по координатной прямой и выберет из них самые большие. Настраиваемся на серьезный лад. Хотя… кто доживет до конца этого урока, все равно будет тихо улыбаться.
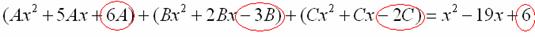
Система готова:
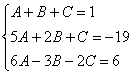
Решаем систему:
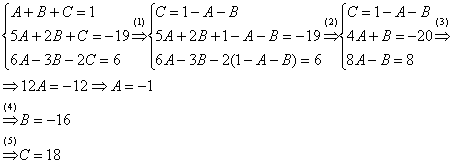
(1) Из первого уравнения выражаем 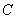 и подставляем его во 2-ое и 3-е уравнения системы. На самом деле можно было выразить
и подставляем его во 2-ое и 3-е уравнения системы. На самом деле можно было выразить 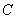 (или другую букву) из другого уравнения, но в данном случае выгодно выразить именно из 1-го уравнения, поскольку там самые маленькие коэффициенты.
(или другую букву) из другого уравнения, но в данном случае выгодно выразить именно из 1-го уравнения, поскольку там самые маленькие коэффициенты.
(2) Приводим подобные слагаемые во 2-ом и 3-м уравнениях.
(3) Почленно складываем 2-ое и 3-е уравнение, при этом, получая равенство 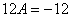 , из которого следует, что
, из которого следует, что 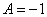
(4) Подставляем 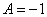 во второе (или третье) уравнение, откуда находим, что
во второе (или третье) уравнение, откуда находим, что 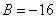
(5) Подставляем 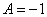 и
и 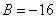 в первое уравнение, получая
в первое уравнение, получая 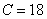 .
.
Если возникли трудности с методами решения системы отработайте их на уроке Как решить систему линейных уравнений?
После решения системы всегда полезно сделать проверку – подставить найденные значения 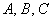 в каждое уравнение системы, в результате всё должно «сойтись».
в каждое уравнение системы, в результате всё должно «сойтись».
Почти приехали. Коэффициенты 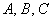 найдены, при этом:
найдены, при этом:
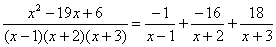
Чистовое оформление задание должно выглядеть примерно так:
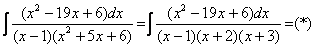
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
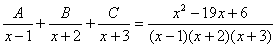
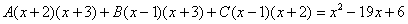
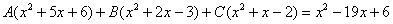
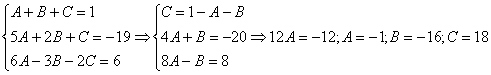

Как видите, основная трудность задания состояла в том, чтобы составить (правильно!) и решить (правильно!) систему линейных уравнений. А на завершающем этапе всё не так сложно: используем свойства линейности неопределенного интеграла и интегрируем. Обращаю внимание, что под каждым из трёх интегралов у нас «халявная» сложная функция, об особенностях ее интегрирования я рассказал на уроке Метод замены переменной в неопределенном интеграле.
Проверка: Дифференцируем ответ:
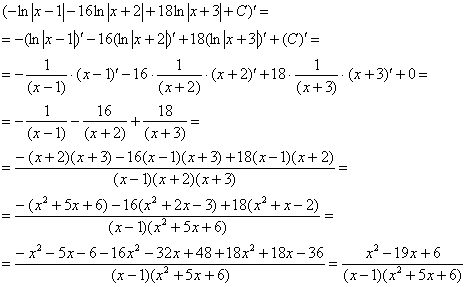
Получена исходная подынтегральная функция, значит, интеграл найдем правильно.
В ходе проверки пришлось приводить выражение к общему знаменателю, и это не случайно. Метод неопределенных коэффициентов и приведение выражения к общему знаменателю – это взаимно обратные действия.
Пример 2
Найти неопределенный интеграл.
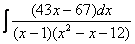
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Вернемся к дроби из первого примера: 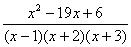 . Нетрудно заметить, что в знаменателе все множители РАЗНЫЕ. Возникает вопрос, а что делать, если дана, например, такая дробь:
. Нетрудно заметить, что в знаменателе все множители РАЗНЫЕ. Возникает вопрос, а что делать, если дана, например, такая дробь: 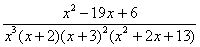 ? Здесь в знаменателе у нас степени, или, по-математически кратные множители. Кроме того, есть неразложимый на множители квадратный трехчлен
? Здесь в знаменателе у нас степени, или, по-математически кратные множители. Кроме того, есть неразложимый на множители квадратный трехчлен  (легко убедиться, что дискриминант уравнения
(легко убедиться, что дискриминант уравнения 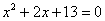 отрицателен, поэтому на множители трехчлен никак не разложить). Что делать? Разложение в сумму элементарных дробей будет выглядеть наподобие
отрицателен, поэтому на множители трехчлен никак не разложить). Что делать? Разложение в сумму элементарных дробей будет выглядеть наподобие 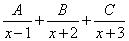 с неизвестными коэффициентами
с неизвестными коэффициентами 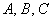 вверху или как-то по-другому?
вверху или как-то по-другому?
Пример 3
Представить функцию 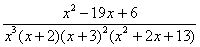 в виде суммы элементарных дробей с неизвестными коэффициентами.
в виде суммы элементарных дробей с неизвестными коэффициентами.
Шаг 1.Проверяем, правильная ли у нас дробь
Старшая степень числителя: 2
Старшая степень знаменателя: 8
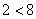 , значит, дробь является правильной.
, значит, дробь является правильной.
Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Очевидно, что нет, всё уже разложено. Квадратный трехчлен 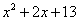 не раскладывается в произведение по указанным выше причинам. Гуд. Работы меньше.
не раскладывается в произведение по указанным выше причинам. Гуд. Работы меньше.
Шаг 3. Представим дробно-рациональную функцию в виде суммы элементарных дробей.
В данном случае, разложение имеет следующий вид:
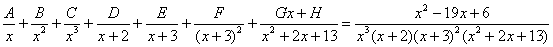
Смотрим на наш знаменатель: 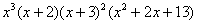
При разложении дробно-рациональной функции в сумму элементарных дробей можно выделить три принципиальных момента:
1) Если в знаменателе находится «одинокий» множитель в первой степени (в нашем случае 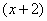 ), то вверху ставим неопределенный коэффициент (в нашем случае
), то вверху ставим неопределенный коэффициент (в нашем случае 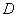 ). Примеры №1,2 состояли только из таких «одиноких» множителей.
). Примеры №1,2 состояли только из таких «одиноких» множителей.
2) Если в знаменателе есть кратный множитель 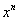 , то раскладывать нужно так:
, то раскладывать нужно так:
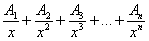 – то есть последовательно перебрать все степени «икса» от первой до энной степени. В нашем примере два кратных множителя:
– то есть последовательно перебрать все степени «икса» от первой до энной степени. В нашем примере два кратных множителя: 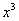 и
и 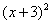 , еще раз взгляните на приведенное мной разложение и убедитесь, что они разложены именно по этому правилу.
, еще раз взгляните на приведенное мной разложение и убедитесь, что они разложены именно по этому правилу.
3) Если в знаменателе находится неразложимый многочлен второй степени (в нашем случае 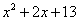 ), то при разложении в числителе нужно записать линейную функцию с неопределенными коэффициентами (в нашем случае
), то при разложении в числителе нужно записать линейную функцию с неопределенными коэффициентами (в нашем случае 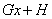 с неопределенными коэффициентами
с неопределенными коэффициентами 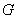 и
и 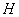 ).
).
На самом деле, есть еще 4-ый случай, но о нём я умолчу, поскольку на практике он встречается крайне редко.
Пример 4
Представить функцию 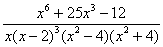 в виде суммы элементарных дробей с неизвестными коэффициентами.
в виде суммы элементарных дробей с неизвестными коэффициентами.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Строго следуйте алгоритму!
Если Вы разобрались, по каким принципам нужно раскладывать дробно-рациональную функцию в сумму, то сможете разгрызть практически любой интеграл рассматриваемого типа.
Пример 5
Найти неопределенный интеграл.
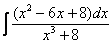
Шаг 1.Очевидно, что дробь является правильной: 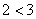
Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Можно. Здесь сумма кубов 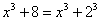 . Раскладываем знаменатель на множители, используя формулу сокращенного умножения
. Раскладываем знаменатель на множители, используя формулу сокращенного умножения 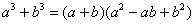
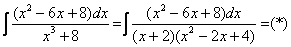
Шаг 3. Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
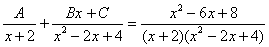
Обратите внимание, что многочлен 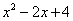 неразложим на множители (проверьте, что дискриминант отрицательный), поэтому вверху мы ставим линейную функцию
неразложим на множители (проверьте, что дискриминант отрицательный), поэтому вверху мы ставим линейную функцию 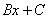 с неизвестными коэффициентами, а не просто одну буковку.
с неизвестными коэффициентами, а не просто одну буковку.
Приводим дробь к общему знаменателю:
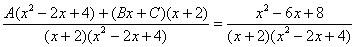
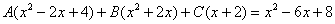
Составим и решим систему:
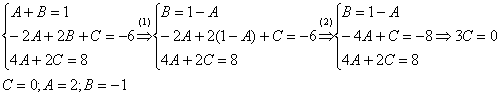
(1) Из первого уравнения выражаем 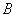 и подставляем во второе уравнение системы (это наиболее рациональный способ).
и подставляем во второе уравнение системы (это наиболее рациональный способ).
(2) Приводим подобные слагаемые во втором уравнении.
(3) Почленно складываем второе и третье уравнения системы.
Все дальнейшие расчеты, в принципе, устные, так как система несложная.
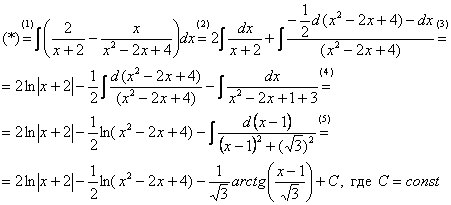
(1) Записываем сумму дробей в соответствии с найденными коэффициентами 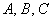 .
.
(2) Используем свойства линейности неопределенного интеграла. Что произошло во втором интеграле? С этим методом Вы можете ознакомиться в последнем параграфе урока Интегрирование некоторых дробей.
(3) Еще раз используем свойства линейности. В третьем интеграле начинаем выделять полный квадрат (предпоследний параграф урока Интегрирование некоторых дробей).
(4) Берём второй интеграл, в третьем – выделяем полный квадрат.
(5) Берём третий интеграл. Готово.
А вот вам еще пара примеров для самостоятельного решения, один похожий, другой – труднее.
Пример 6
Найти неопределенный интеграл.
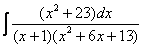
Пример 7
Найти неопределенный интеграл.