Пример приведения общего уравнения линии второго порядка к каноническому виду

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Кривые второго порядка. 2

Пример приведения общего уравнения линии второго порядка к каноническому виду 2

Эллипс. 5

Вывод уравнения эллипса. 5

Гипербола. 7

Парабола. 8

Примеры решения задач на тему «Кривые второго порядка». 9

Кривые второго порядка

Общее уравнение кривой второго порядка в декартовой системе координат имеет вид

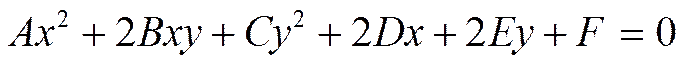
A, B, C – одновременно не равны нулю.

Важнейшие случаи общего уравнения кривой II порядка.

1. Эллипс: 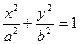, ( 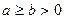). При 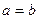- окружность. ;

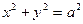2. Гипербола: 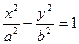, ( 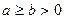) с полуосями 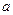и ;

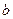3. Парабола: , ( );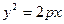

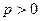4. Пара пересекающихся прямых: , ( )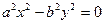

, ;

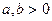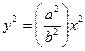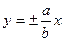5. Пара параллельных или совпадающих прямых: , ( )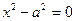

;

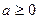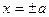6. Точка: .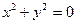

Могут быть случаи, когда нет точек, удовлетворяющих уравнению:

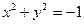- мнимая кривая II порядка (эллипс мнимый);

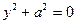- пара мнимых параллельных прямых.

Пример приведения общего уравнения линии второго порядка к каноническому виду

(*)

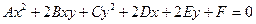В большинстве формул теории линий второго порядка коэффициенты 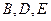входят деленными на 2, т. е. буквы 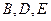обозначают половину коэффициента. Первые три члена уравнения называются старшими членами.

Можно записать уравнение (*) следующим образом:

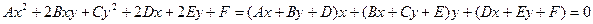
Пусть дано общее уравнение II порядка (*). Требуется упростить это уравнение путём перехода к другой системе координат (с более выгодным расположением осей):

1) добиться, чтобы число членов первой степени стало наименьшим;

2) в группе старших членов избавиться от слагаемого с произведением координат;

3) избавиться от свободного члена.

Для этого воспользуемся параллельным переносом и поворотом координатных осей.

Выведем формулы преобразования координат при параллельном переносе и повороте осей. Пусть точка 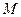имеет координаты 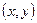в «старой системе координат» и 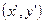– в новой системе координат, полученной путем параллельного переноса и последующего поворота осей.

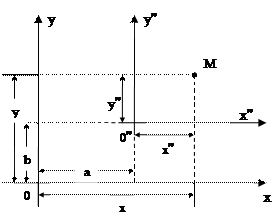Параллельный перенос координатных осей

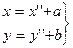(1)

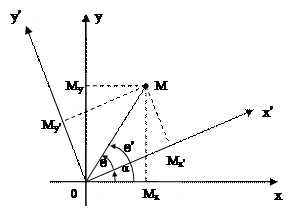Поворот координатных осей

Пусть ,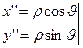

.

,

.

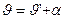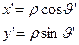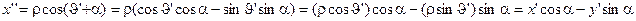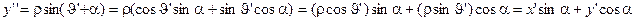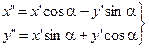(2)

Формулы (1) и (2) задают старые координаты точки через ее координаты в новой системе.

Рассмотрим приведение общего уравнения линии второго порядка к каноническому виду на примере.

Пусть дано общее уравнение второго порядка:

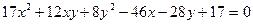. (3)

Произведем параллельный перенос координатных осей в точку 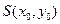по формулам (1): .

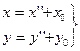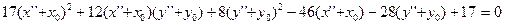
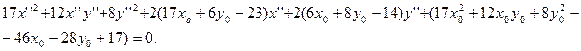(3’)

Чтобы избавиться от членов первого порядка, приравняем коэффициенты при них к нулю:

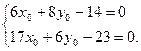
Решив систему, найдем координаты точки S 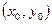, нового начала координат: S 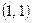. Подставим эти координаты в уравнение (3’). В новых координатах уравнение примет вид:

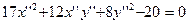(4)

Геометрический смысл преобразования – перенести начало координат в центр кривой.

Осталось повернуть оси, чтобы они совпали с осями симметрии кривой. Воспользуемся формулами поворота координатных осей (2).

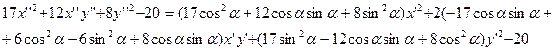(5)

Подбираем угол 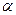так, чтобы коэффициент при произведении 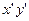стал равен нулю, т. е. решаем уравнение

.

,

.

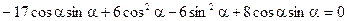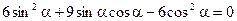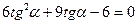Определяем 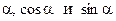и подставляем в (5):

.

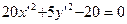Приводим уравнение к каноническому виду, разделив все коэффициенты на 20:

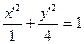. (6)

Уравнение (6) – это каноническое уравнение эллипса с полуосями 2 (по оси О 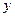) и 1(по оси О ).

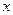Эллипс

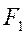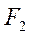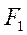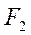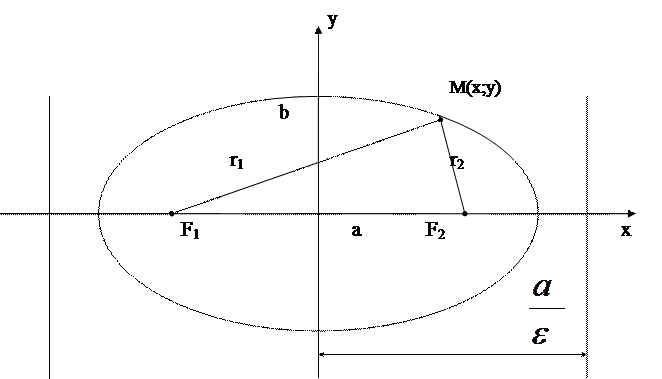
Определение. Эллипс – это геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости и есть постоянная величина. Точки и называются фокусам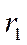и.

и 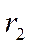- фокальные радиусы точки .

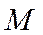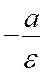
0

, ,

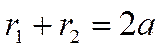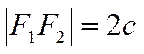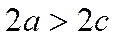следовательно ,

.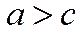
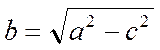