Свойства многочленов в двоичном поле GF(2)

1. Ненулевые элементы поля GF(2ⁿ) являются корнями

_n

обобщенного многочлена X ^{2 – 1} + 1.

2. Каждый многочлен р (Х) степени n, неприводимый над полем

_n

Галуа GF(2) является делителем двучлена X ^{2 – 1} + 1, и каждый

_n

делитель двучлена X ^{2 – 1} + 1, неприводимый над полем GF(2), имеет степень, равную n и менее.

3. Все элементы поля GF(2 ⁿ) можно получить как совокупность остатков от деления 100…00 на неприводимый многочлен р (Х),

_n

входящий в разложение двучлена (X ^{2 – 1} + 1). Эти остатки –

_n

корни двучлена (X ^{2 – 1} + 1), т.е. обращают его в нуль. Число остатков равно (2 ⁿ – 1).

4. В поле GF(2 ⁿ) существует примитивный элемент a, такой, что каждый ненулевой элемент поля GF(2 ⁿ) может быть представлен как некоторая степень a, т.е. мультипликативная группа GF(2 ⁿ) является циклической.

Пример. Определение элементов a_i поля GF(2 ⁴).

Согласно свойству 1 ненулевые элементы поля GF(2 ⁴) являются

₄

корнями обобщенного двучлена (X ^{2 – 1} + 1) = (Х ¹⁵ + 1). Двучлен (Х ¹⁵ + 1) можно представить в виде произведения неприводимых многочленов – сомножителей:

(Х ¹⁵ + 1) = Р (Х ¹) • Р (Х ²) • Р₁ (Х ⁴) • Р₂ (Х ⁴) • Р₃ (Х ⁴),

где:

Р (Х ¹) = Х + 1,

Р (Х ²) = Х ² + Х + 1,

Р₁ (Х ⁴) = Х ⁴ + Х + 1,

Р₂ (Х ⁴) = Х ⁴ + Х ³ + 1,

Р₃ (Х ⁴) = Х ⁴ + Х ³ + Х ² + Х + 1.

В соответствии со свойством 3 вычислим элементы a_i поля GF(2 ⁴) как совокупность остатков от деления 100…00 на неприводимый многочлен Р₁ (Х ⁴) = Х ⁴ + Х + 1.

Процедура определения остатков.

Делят на Р₁ (Х ⁴) = Х ⁴ + Х + 1 Û 10011 единицу с возрастающим числом нулей, т.е. делят одночлены Х ^j, где j = 0, 1, 2, 3, …, на многочлен Х ⁴ + Х + 1. Степени одночленов Х ⁰, Х ¹, Х ², Х ³ меньше степени многочлена Р₁ (Х ⁴), поэтому первые четыре остатка от деления на Р₁ (Х ⁴) равны делимым, т.е. одночленам Х ⁰, Х ¹, Х ², Х ³.

Для одночлена Х ⁴ Û 10000 получаем остаток:

Å
	Û Х 4

Для одночлена Х ⁵ Û100000 получаем остаток:

Å
	Û Х 5

Таким образом, схема вычисления остатков:

Å   Å   Å   Å   Å   Å   Å   Å
	Û Х 4
	Û Х 7
	Û Х 8
	Û Х 10
	Û Х 12
	Û Х 13
	Û Х 14
	Û Х 15 = Х 0

Результаты занесем в таблицу 1.9.1.

Таблица 1.9.1 – Вычисленные остатки и нулевые элементы a₀ - a₁₄ поля Галуа GF(2 ⁴)

Х j	Остаток	ai
Х 0		a0
Х 1		a1
Х 2		a2
Х 3		a3
Х 4		a4
Х 5		a5
Х 6		a6
Х 7		a7
Х 8		a8
Х 9		a9
Х 10		a10
Х 11		a11
Х 12		a12
Х 13		a13
Х 14		a14

Поле Галуа GF(2⁴) построено как поле многочленов с коэффициентами 0 и 1 по модулю неприводимого многочлена

Р₁ (Х ⁴) = Х ⁴ + Х + 1 Û 10011.

В поле Галуа GF(2 ⁿ) определены четыре алгебраические операции.

Операции сложения и вычитания выполняются как операции поразрядного сложения по модулю 2.

Операция умножения элементов поля выполняется как умножение соответствующих многочленов с приведением по модулю неприводимого многочлена Р (Х), т.е. многочлена, по модулю которого построены элементы поля GF(2 ⁿ).

Пример. a₅ = 0110, a₆ = 1100, a₅ + a₆ = 1010, так как

Å

Пример. a₁₄ = 1001, a₁₄ • a₁₄ = a₁₃ по mod P₁ (X⁴) Û 10011.

	•
Å 1001

Å
	Û a13

Чтобы выполнить деление элемента b на элемент а в поле GF(2 ⁿ) по модулю Р(Х), сначала находят обратный элемент а ^{– 1} (mod P (X)), а затем вычисляют

b • a ^{– 1} (mod P (X)).

Каждый двоичный вектор длиной n, исключая 0, является взаимно простым с неприводимым многочленом Р (Х) независимо от значения

Р (Х). Поэтому число вычетов, взаимно простых с Р (Х), равно

j (Р(Х)) = 2 ⁿ – 1 (расширение фугкции Эйлера для многочленов). Поэтому

_n

a ^{– 1} = a ^{j (Р(Х)) – 1} mod P (X) = a ^{2 – 2} mod P (X).

Пример. Пусть а = 100 и Р (Х) = 1011 в поле Галуа GF(2 ³).

₃

a ^{– 1} = 100 ^{2 – 2} (mod 1011) = 100 ⁶ (mod 1011) = 100 ² •100 ⁴ (mod 1011).

100 ² (mod 1011) = 10000 Å 10110 = 110

или

Å

100 ⁴ (mod 1011) = 110 ² (mod 1011) = 010

или

	•
Å 000

Å

100 ² •100 ⁴ (mod 1011) = 110 • 010 (mod 1011) = 1100 (mod 1011) = 111

или

Å

Итак, а ^{– 1} = 111.

Проверка: а = 100, а ^{– 1} = 111, Р (Х) = 1011, а • а ^{– 1} = 110 • 100 = 11100.

Å   Å

т.е. а • а ^{– 1}(mod 1011) = 1.

1.10 Достоинства вычислений в поле Галуа GF(2 ⁿ)

1. Все элементы поля Галуа имеют конечный размер, деление элементов не имеет каких-либо ошибок округления.

2. Сложение и вычитание элементов поля GF(2 ⁿ) не требует деления на модуль.

3. Алгоритмы вычислений в поле GF(2 ⁿ) допускают параллельную реализацию.

4. Для поля GF(2 ⁿ) обычно применяют в качестве модуля трехчлен Р (Х ⁿ) = Х ⁿ + X + 1.

Длинная строка нулей между коэффициентами при Х ⁿ и X обеспечиваетболее простую реализацию быстрого умножения (с приведением по модулю). Трехчлен Р (Х ⁿ) должен быть неприводимым и примитивным.

Трехчлен Р (Х ⁿ) = Х ⁿ + X + 1 является примитивным для следующих значений n (n < 1000):

1, 3, 4, 6, 9, 15, 22, 28, 30, 46, 60, 63, 127, 153, 172, 303, 471, 532, 865, 900.

КОДИРОВАНИЕ

Оптимальное кодирование

Оптимальным кодированиемназывается процедура преобразования символов первичного алфавита m₁ в кодовые слова во вторичном алфавите m₂, при котором средняя длина сообщений во вторичном алфавите имеет минимально возможную длину.

Коды, представляющие первичные алфавиты с неравномерным распределением символов, имеющие среднюю минимальную длину кодового слова во вторичном алфавите, называются оптимальными неравномерными кодами (ОНК).

Эффективность ОНК оценивают при помощи двух коэффициентов:

1. коэффициента статического сжатия

,

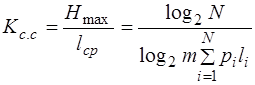который характеризует уменьшение количества двоичных знаков на символ сообщения при применении ОНК по сравнению с применением методов нестатистического кодирования.

2. коэффициента относительной эффективности

,

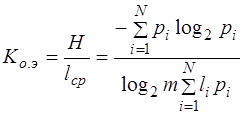который показывает, насколько используется статическая избыточность передаваемого сообщения.

Из свойств оптимальных кодов вытекают принципы их построения:

· выбор каждого кодового слова необходимо производить так, чтобы содержащееся в нем количество информации было максимальным,

· буквам первичного алфавита, имеющим большую вероятность, присваиваются более короткие кодовые слова во вторичном алфавите.

Принципы оптимального кодирования определяют методики построения оптимальных кодов.

I. Построение ОНК по методике Шеннона-Фано для ансамбля из M сообщений сводится к следующей процедуре:

1) множество из M сообщений располагают в порядке убывания вероятностей;

2) первоначальный ансамбль кодируемых сигналов разбивают на две группы таким образом, чтобы суммарные вероятности сообщений обеих групп были по возможности равны;

3) первой группе присваивают символ 0, второй группе символ 1;

4) каждую из подгрупп делят на две группы так, чтобы их суммарные вероятности были по возможности равны;

5) первым подгруппам каждой из групп вновь присваивают 0, а вторым - 1, в результате чего получают вторые цифры кода. Затем каждую из четырех подгрупп вновь делят на равные (с точки зрения суммарной вероятности) части и т. д. До тех пор, пока в каждой из подгрупп останется по одной букве.

Алгоритм 2.1.1 – Алгоритм построения кода, близкого к оптимальному

Вход :Р : array[1..n] of real -массив вероятностей появления букв в сообщении, упорядоченный по убыванию; 1 ³ Р [1] ³ … ³ Р [n] > 0,

Р [1] + … + Р [n] = 1.

Выход :С : array[1..n, 1..L] of0..1-массив элементарных кодов.

Fano (1, n, 0) {вызов рекурсивной процедуры Fano}

Основная работа по построению элементарных кодов выполняется следующей рекурсивной процедурой Fano.

Вход: b - индекс начала обрабатываемой части массива P,

e - индекс конца обрабатываемой части массива P,

k - длина уже построенных кодов в обрабатываемой части массива C.

Выход: заполненный массив С.

ife > bthen

k : = k + 1 {место для очередного разряда в коде}

m : = Med (b, e) {деление массива на две части}

fori frombtoe do

C [i, k] : = i > m {в первой части добавляем 0, во второй – 1}

End for

Fano (b, m, k) {обработка первой части}

Fano (m + 1, е, k) {обработка второй части}

End if

Функция Med находит медиану указанной части массива Р [b..e], т.е. определяет такой индекс m (b ≤ m < e), что сумма элементов Р [b..m] наиболее близка к сумме элементов Р [m + 1..e].

Примечание. При каждом удлинении кодов в одной части коды удлиняются нулями, а в другой части – единицами. Таким образом, коды одной части не могут быть префиксами другой. Удлинение кода заканчивается тогда и только тогда, когда длина части равна 1, то есть остается единственный код. Таким образом, схема построения префиксная, а потому разделимая, т.е. коды не требуют разделителя.

Пример: Построим оптимальный код сообщения, состоющего из восьми равновероятных букв.

Решение. Так вероятности данного ансамбля сообщений равны p₁ = = p₂ = ...= p₈ = 2^-3 и порядок их расположения не играет роли, то расположим их так, как показано в таблице 2.1.1. Затем разбиваем данное множество на две равновероятные группы. Первой группе в качестве первого символа кодовых слов присваиваем 0, а второй - 1. Во второй колонке таблицы записываем четыре нуля и четыре единицы. После чего разбиваем каждую из групп еще на две равновероятные подгруппы. Затем каждой первой подгруппе присваиваем 0, а второй - 1 и записываем в третью колонку таблицы. Далее каждую из четырех подгрупп разбиваем на две равновероятные части и первой из них присваиваем 0, а второй - 1. Таким образом в четвертой колонке появится значение третьего символа кодовых слов.

Таблица 2.1.1 – Оптимальный код равновероятных букв

Буква	Кодовое слово полученное после разбиения
	первого	второго	третьего
А1 А2 А3 А4 А5 А6 А7 А8

Проверка оптимальности кода осуществляется путем сравнения энтропии кодируемого (первичного) алфавита со средней длиной кодового слова во вторичном алфавите.

Для рассматриваемого примера энтропия источника сообщений

H = log₂ N = log₂ 8=3 бит/символ

а среднее число двоичных знаков на букву кода

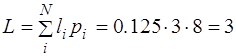бит

где l_i - длина i-ой кодовой комбинации; p_i - вероятность появления i-го символа комбинации длиной в l_i.

Таким образом, H = L, т. е. код является оптимальным для данного ансамбля сообщений.

Вывод: Для ансамблей равновероятных сообщений оптимальным является равномерный код. Если число исходных элементов ансамбля равно целой степени двух, то всегда H = L.

Пример. Первичный алфавит состоит из 8 символов со следующими вероятностями появления: a₁ = 0,5; a₂ = 0,25; a₃ = 0,098; a₄ = = 0,052; a₅ = 0,04; a₆ = 0,03; a₇ = 0,019; a₈ = 0,011. Построить ОНК по методу Шеннона - Фано и подсчитать коэффициенты.

Решение проиллюстрируем в таблице 2.1.2.

Таблица 2.1.2 – Оптимальный код неравновероятных букв

ai	pi	Кодовое слово после разбиения	Знаков	lipi
	0,5		-	-	-	-	-		0,5
	0,25			-	-	-	-		0,5
	0,098					-	-		0,392
	0,052					-	-		0,208
	0,04					-	-		0,16
	0,03						-		0,15
	0,019								0,114
	0,011								0,066

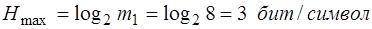
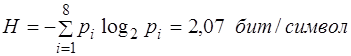
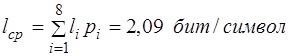
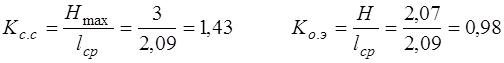
Недостатком методики Шеннона – Фано является неоднозначность построения ОНК. В методике Хаффмена этого недостатка нет.

ІІ. Хаффмен предложил следующий метод построения ОНК:

1) Символы первичного алфавита выписываются в порядке убывания вероятностей.

2) Последние n₀ символов, где 2 £ n₀ £ m и N - n₀ / m - 1 - целое число, объединяют в некоторый новый символ с вероятностью, равной сумме вероятностей объединяемых символов.

3) Последние символы с учетом образованного символа вновь объединяют и получают новый, вспомогательный, символ.

4) Опять выписывают символы в порядке убывания вероятноьстей с учетом вспомогательного символа и т. д. До тех пор, пока вероятности m оставшихся символов после N - n₀/m - 1-го выписывания не дадут в сумме 1.

На практике обычно не производят многократного выписывания вероятностей символов, а обходятся элементарными геометрическими построениями, суть которых для кодов с числом качественных признаков m = 2 сводится к тому, что символы кодируемого алфавита попарно объединяются в новые символы, начиная с символов, имеющих наименьшую вероятность, а затем, с учетом вероятностей вновь образованных символов, опять производят попарное объединение символов с наименьшими вероятностями и таким образом строят двоичное кодовое дерево, в вершине которого стоит символ с вероятностью 1.

Пример.

Построить методом Хаффмена оптимальный код для алфавита со следующим распределением вероятностей появления букв в тексте: A = 0,5; B = 0,15; C = 0,12; D = 0,1;

E =0,04; F = 0,04; G = 0,03;

H = 0,02.

Решение.

Сначала находят буквы с наименьшими вероятностями 0,02 (H) и 0,03 (G), затем проводят от них линию к точке, в которой вероятность появления буквы G равна 0,05. Затем берут две наименьшие вероятности 0,04 (F) и 0,04 (E) и получают новую точку с вероятностью 0,08.

Теперь наименьшими вероятностями обладают точки, соответствующие вспомогательным символам с вероятностями 0,05 и 0,08. Соединяем их линией с новой точкой, соответствующей вспомогательному символу с вероятностью 0,13.

Продолжаем алгоритм до тех пор, пока линия от основных и вспомогательных символов не сольются в точке, дающую суммарную вероятность, равную 1.

Обозначим каждую верхнюю линию (см. рисунок 2.1.1) цифрой 1, а нижнюю - цифрой 0. Получим ОНК, который для каждого слова представляет собой последовательность нулей и единиц, которые встречаются по пути к данному слову от конечной точки (1,00).

Полученные коды представлены в таблице 2.1.3.

Таблица 2.1.3 – Двоичный код Хаффмена для восьми сообщений

Буква	Вероятность	ОНК	Число знаков в кодовом слове	pili
A B C D E F G H	0,50 0,15 0,12 0,10 0,04 0,04 0,03 0,02	0 0 1 0 1 1 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0		0,50 0,45 0,36 0,30 0,20 0,20 0,15 0,10

Пример.

Построить код Хаффмена для передачи сообщений при помощи трех частот f₁, f₂, f₃, если символы первичного алфавита встречаются в сообщениях со следующими вероятностями: А = 0,24; Б = 0,18; В = 0,38;

Г = 0,1; Д = 0,06; Е = 0,02; Ж = 0,02.

Решение.

Таблица 2.1.4 – Троичный код Хаффмена для семи сообщений

Буква	Вероятность	Дерево	Код
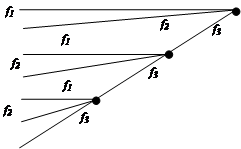В А Б Г Д Е Ж	0,38 0,24 0,18 0,1 0,06 0,02 0,02		f1 f2 f3f1 f3f2 f3f3f1 f3f3f2 f3f3f3

Полученный код легко декодируется, так как ни один код не начинается с f₁ и f₂, кроме одного одноразрядного кода.

Алгоритм 2.1.1 – Алгоритм построения оптимального кода – рекурсивная процедура Huffman

Вход :n – количество букв, Р : array[1..n] of real -массив вероятностей появления букв в сообщении, упорядоченный по убыванию; 1 ³ Р [1] ³ … ³ Р [n] > 0, Р [1] + … + Р [n] = 1.

Выход :С : array[1..n, 1..L] of0..1-массив элементарных кодов.

l : array[1..n] of1..L – массив длин элементарных кодов схемы префиксного кодирования.

ifn = 2then

C [1, 1]: = 0; l [1]: = 1 {первый элемент}

C [2, 1]: = 1; l [2]: = 1 {второй элемент}

Else

q : = P [n – 1]+ P [n] {сумма двух последних вероятностей}

j : = Up (n, q ) {поиск места и вставка суммы}

Huffman (P, n – 1) {рекурсивный вызов}

Down (n, j) {достраивание кодов}

End if

Примечание. Функция Up находит место в массиве Р, в котором должно находиться число q и вставляет это число, сдвигая вниз остальные элементы. Процедура Down строит оптимальный код для n букв на основе построенного оптимального кода для n – 1 буквы. Для этого код буквы с номером j временно исключается из массива С путем сдвига вверх кодов букв с номерами, большими j, а затем в конец обрабатываемой части массива С добавляется мара кодов, полученных из кода буквы с номером j удлинением на 0 и 1, соответственно.

Для пары букв при любом распределении вероятностей оптимальное кодирование очевидно: первой букве нужно назначить код 0, а второй – 1. Именно это и делается в первой части оператора ifосновной процедуры Huffman. С помощью функции Up в исходном упорядоченном массиве Р отбрасываются две последние (наименьшие) вероятности, и их сумма вставляется в масси Р, так чтобы массив (на единицу меньшей длины) остался упорядоченным. При этом место вставки сохраняется в локальной переменной j. Так происходит до тех пор, пока не останется массив из двух элементов, для которого оптимальный код известен. После этого в обратном порядке строятся оптимальные коды для трех, четырех и т.д. элементов. При этом масси вероятностей Р уже не нужен – нужна только последовательсноть номеров кодов, которые должны быть изъяты из массива кодов и продублированы в конце с добавлением рахряда. А эта последовательность хранится в экземплярах локальной переменной j, соответствующих рекурсивным вызовампроцедуры Huffman.

Данный алгоритм можно использовать для сжатия файлов. Причем, если учитывать все 256 ASCII символов, то разницы в сжатии, например, *.txt и *.exe не будет.

К недостаткам алгоритма относятся:

1. Необходимость при кодировании двукратного прочтения файла первый раз для подсчета частоты вхождения символов,

второй – непостредственно для кодирования.

2. Необходимость хранения вместе с сжатым файлом декодирующего дерева для возможности восстановления файла.