Предел монотонной ограниченной функции

РАЗДЕЛ 2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИЙ И ОТОБРАЖЕНИЙ

· Рассматриваются важные для дальнейшего погятия предельного перехода и непрерывности

· Рассматриваются понятия предела последовательности, предела функции, отображения, непрерывности функции. отображения. Описываются необхъодимые свойства этих понятий

ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНО МАЛЫЕ ВЕЛИЧИНЫ. АРИФМЕТИЧЕСКИЕ СВОЙСТВА ПРЕДЕЛА

Определение.Если каждому сопоставлено число , то говорят, чтозадана последовательность

Некоторые последовательности обладают очень важным свойством – они имеют предел.

Определение.Последовательность имеет предел, равный числу A тогда и только тогда, когда для любого существует число такое, что для всех , удовлетворяющих неравенству , выполняется неравенство .

Удобно записывать это определение с помощью логических символов: .

Для обозначения предела последовательности используется символ: .

Пусть определена в некоторой проколотой окрестности точки а.

Определение.Функция имеет при предел, равный числу А тогда и только тогда, когда для любой окрестности точки А существует проколотая окрестность точки а такая, что , или, равносильно, такая, что для любого . С помощью логических символов это определение записывается так:

Данное определение называется определением предела по Коши.

В этом определении можно вместо произвольной рассматривать при произвольном и, соответственно, вместо - проколотую окрестность . Тогда оно примет вид: .

Вспоминая, что условие равносильно неравенствам , а условие равносильно условию , получаем равносильную запись определения предела на "языке ":

Теорема.

1) Если предел последовательности существует, то он единственен, т.е. если и если , то

2) Если предел функции имеет при существует, то он единственен, т.е. , , то

Определение.Последовательность называется бесконечно малой, если . Аналогично, функция - бесконечно малая при , если .

Теорема.Предел последовательности существует и равен А тогда и только тогда, когда можно представить в виде , где - бесконечно малая последовательность.

Аналогично, тогда и только тогда, когда , где - бесконечно малая при функция.

Определение.Функция называется ограниченной при , если она ограничена в некоторой , т.е. если : .

Теорема. (Свойства бесконечно малых)

1. Если и - бесконечно малые при , то алгебраическая сумма - тоже бесконечно малая при ;
2. Если - бесконечно малая и - ограниченная при , то произведение есть бесконечно малая при ;
3. Если и - бесконечно малые при , то произведение - тоже бесконечно малая при .

Бесконечно малые последовательности обладают вполне аналогичными свойствами:

1. Если и - бесконечно малые последовательности, то алгебраическая сумма - тоже бесконечно малая последовательность;
2. Если - бесконечно малая последовательность, а - ограниченная последовательность (т.е. : ), то - бесконечно малая последовательность;
3. Если и - бесконечно малые последовательности, то произведение - бесконечно малая последовательность.

Теорема(Арифметические свойства предела)

Пусть две функци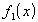и и 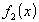, имеют пределы и , соответственно, при . Тогда предел суммы, разности, произведения, и, если , частного этих функций равны соответственно сумме, разности, произведению и частному значения этих пределов, т.е. , если , то .

Аналогично теорема верна и для последовательностей. Если , то , то , а если , то и .

ПРЕДЕЛЬНЫЙ ПЕРЕХОД В НЕРАВЕНСТВАХ

Теорема .Если функция имеет предел при , равный А и в некоторой проколотой окрестности точки a принимает неотрицательные значения, то .

Теорема.Если для двух функций и , имеющих пределы, соответственно, и , в некоторой проколотой окрестности выполняется неравенство , то .

Замечание:Эти две теоремы означают, что при переходе к пределу сохраняется нестрогое неравенство.

Замечание: строгое неравенство между функциями может не сохраниться для пределов.

Например, для функций , в любой выполняется неравенство , т.е. . Однако,

Теорема.(Теорема о “зажатой” переменной). Если выполняется неравенство , и если , то

Определение.Если , то говорят, что существует предел функции при стремлении х к а справа и обозначают это так: . Аналогично, если , то говорят, что существует предел функции при стремлении х к а слева и обозначают это так: .

Теорема.Функция имеет при предел, равный а, тогда и только тогда, когда он имеет пределы при стремлении х к а справа и слева, причем оба эти пределы равна А.

Замечание.Разумеется, для пределов справа и слева верны все теоремы об арифметических свойствах предела и о предельном переходе в неравенствах.

Ниже приводятся определения бесконечных пределов.

.

.

.

.

.

ПРЕДЕЛ МОНОТОННОЙ ОГРАНИЧЕННОЙ ФУНКЦИИ

Определение.Последовательность называется неубывающей , если для всех n выполняется неравенство . Она называется возрастающей, если выполняется неравенство . Последовательность называется невозрастающей , если для всех n выполняется неравенство . Она называется убывающей, если выполняется неравенство .Общее название всех таких последовательностей – монотонные последовательности.

Определение.Функция , определенная на промежутке называется: неубывающей(возрастающей) на Х, если для всех из неравенства следует неравенство ( ). Она называется невозрастающей(убывающей) на Х, если из следует ( ). Общее название для этих случаев – монотонные на Х функции.

Теорема . (К. Вейерштрасс)

1. Если последовательность не убывает и ограничена сверху, то существует .
2. Если последовательность не возрастает и ограничена снизу, то существует .

Теорема . (К. Вейерштрасс)

1) Если не убывает на и ограничена сверху на , то существует .

2) Если не убывает на и ограничена снизу на , то существует .

3) Если не возрастает на и ограничена сверху, то существует .

4) Если не возрастает на и ограничена снизу, то существует .

Следствие. Если - монотонная на функция, то для любого существуют и .