Промежуточные значения непрерывной на отрезке функции

Определение.Пусть функция 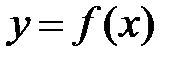определена на некотором множестве 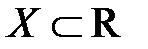. Если она непрерывна в каждой точке этого множества, то говорят, что она непрерывна на множестве 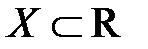.Иными словами, функция 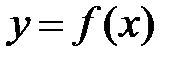непрерывна на множестве 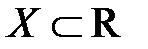, если для любого числа 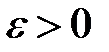и любого 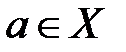существует такое число 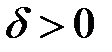, что для всех 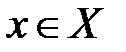, удовлетворяющих неравенству 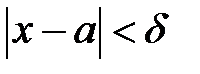выполняется неравенство .

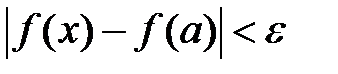Теорема.(Больцано, Коши)Пусть функция 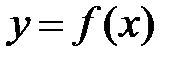непрерывна на отрезке 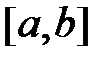и принимает на его концах значения разных знаков. Тогда существует хотя бы одна точка 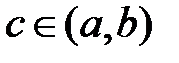такая, что .

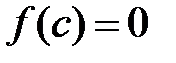Следствие.Пусть функция непрерывна на отрезке , и пусть ( ). Тогда для любого числа , удовлетворяющего неравенствам ( ), существует точка такая, что .

$ Рассмотрим функцию 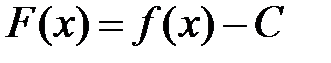. Она непрерывна на отрезке 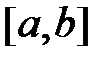как разность непрерывной по условию функции 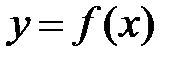и постоянной функции. 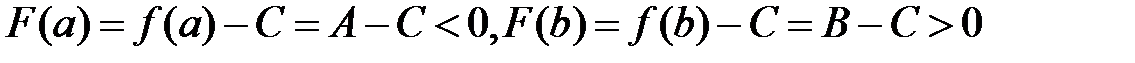, поэтому существует точка 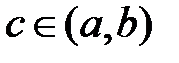такая, что 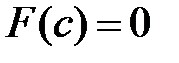, т.е. .#

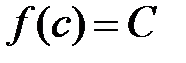ОГРАНИЧЕННОСТЬ НЕПРЕРЫВНОЙ НА ОТРЕЗКЕ ФУНКЦИИ

Теорема.(Вейерштрасс) Пусть функция 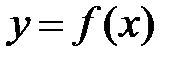непрерывна на отрезке 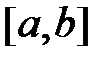. Тогда она ограничена на этом отрезке.

Замечание.Если функция 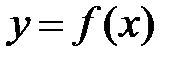непрерывна на интервале 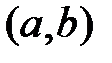, то она может быть неограниченной на этом интервале. Например, функция 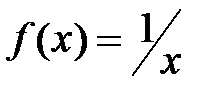на интервале 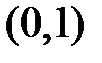непрерывна. Однако для любого числа 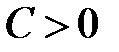имеет место неравенство 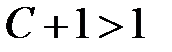, откуда 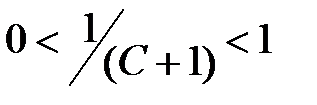и значение этой функции в точке 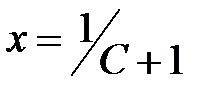равно .

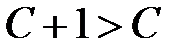Следствие.Пусть функция 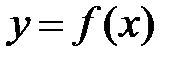непрерывна на отрезке 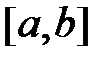. Тогда существуют точная верхняя грань 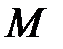и точная нижняя грань 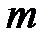множества её значений на отрезке .

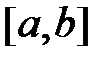Теорема.(Вейерштрасс) Пусть функция 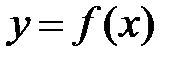непрерывна на отрезке 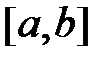. Тогда существуют такие точки 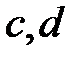, принадлежащие этому отрезку, что .

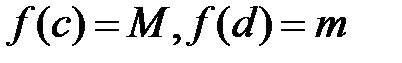Замечание.Часто эту теорему формулируют так:

Непрерывная на отрезке функция принимает свои наименьшее и наибольшее значения на этом отрезке.

Следствие. Пусть функция 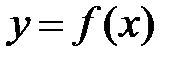непрерывна на отрезке 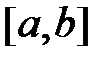. Тогда для любого числа 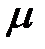, удовлетворяющего неравенствам 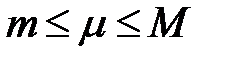, существует точка 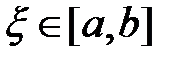такая, что .

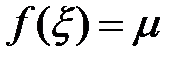Замечание.Доказанные утверждения означают, что непрерывная на отрезке функция принимает на нём все свои значения, от наименьшего до наибольшего. Разумеется, таким свойством могут обладать не только непрерывные функции. Например, функция 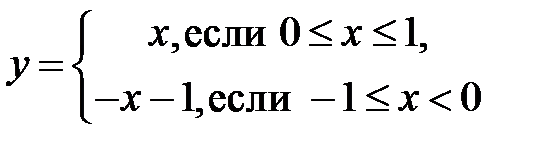принимает все значения от -1 до +1, однако имеет разрыв в точке .

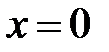Теорема.Пусть функция 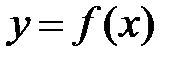непрерывна на промежутке 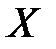(конечном или бесконечном). Тогда множество её значений 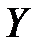также представляет собой промежуток.

Обратная функция

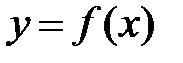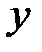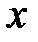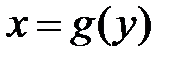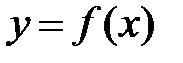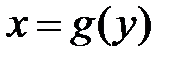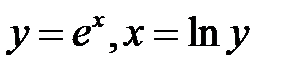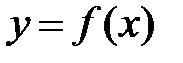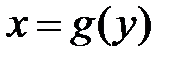Обратная функция – частный случай понятия обратного отображения. Если задана функция , обладающая тем свойством, что любое своё значение она принимает при единственном значении , то это даёт возможность рассматривать обратную функцию , такую, что равенства и равносильны . Примером служат функции . Ясно, что обе функциональные зависимости, и определяют одну и ту же кривую на плоскости. Часто рассматривают функцию 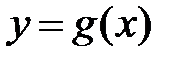( и именно эту функцию называют обратной). График такой функции получается из графика функции 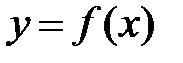отражением относительно биссектрисы первого координатного угла.

Теорема.Пусть функция 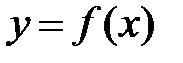возрастает (убывает) на промежутке 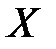. Тогда на промежутке 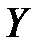, представляющем собой множество её значений, определена обратная функция 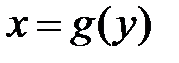, которая также возрастает(убывает) и непрерывна.

РАВНОМЕРНАЯ НЕПРЕРЫВНОСТЬ

Определение.Пусть функция 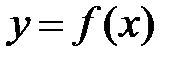определена на некотором множестве 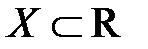. Функция 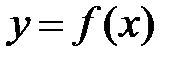называется равномерно непрерывной на множестве 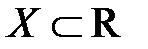, если для любого числа 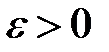существует такое число 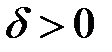, что для всех 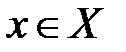и 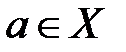удовлетворяющих неравенству 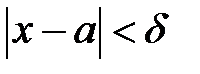выполняется неравенство .

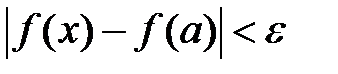Замечание.Есть важное различие между понятиями равномерной непрерывности на множестве 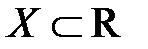и непрерывности на этом множестве. Из равномерной непрерывности следует непрерывность, но не наоборот. В определении равномерной непрерывности содержится сильное требование о том, чтобы входящее в определение число 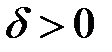зависело только от числа 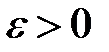. В обычном определении непрерывности на множестве ( определение 16.1) это число 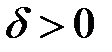зависит не только от числа 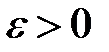, но ещё и от точки 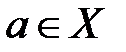. Поэтому возможно, что общего значения числа 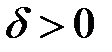, одновременно пригодного для всех 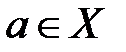, найти не удастся. Однако если в качестве множества 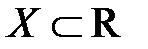рассматривается отрезок числовой оси, то верна такая теорема.

Теорема.(Кантор)Пусть функция 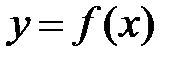непрерывна на отрезке 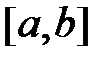. Тогда она равномерно непрерывна на этом отрезке.

Замечание.Функция, непрерывная на интервале 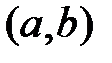, не обязательно равномерно непрерывна на нём. Пример: функция 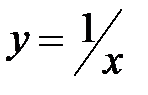, непрерывная на интервале 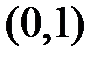, не равномерно непрерывна на этом интервале. Для доказательства выберем 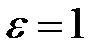и для любого 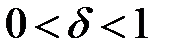рассмотрим точки 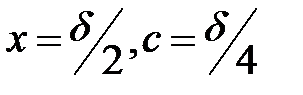. При этом 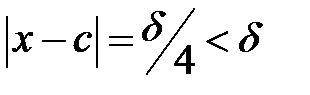, но 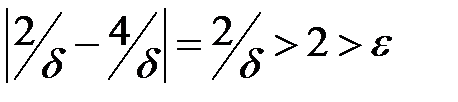.