Тема 2. ПОНЯТИЕ КАК ФОРМА МЫШЛЕНИЯ

ЮФ - 104

Тема 1. ЛОГИКА И ЯЗЫК ПРАВА

Основные этапы развития логики. Предмет и значение логики. Логика в сфере права. Логическая семантика. Взаимосвязь мышления и языка. Гипотеза Сепира-Уорфа. Имена, предикаторы, предложения. Смысл и значение языковых выражений. Язык и метаязык. Понятие логической формы. Язык классической логики предикатов.

Упражнения

Из приведенных понятий построить ряды, в которых каждое последующее понятие было бы родовым по отношению к предыдущему.

· Преступление, книга, животное, уголовное преступление, сооружение, наука, печатное издание, млекопитающее, живой организм, здание, интересная книга, логика, новое здание, аристотелевская логика.

2. Выявить отношения между объемами понятий:

* отличник учебы – гражданин РФ

* студент вуза – учащийся

логика – философская наука

понятие - форма мышления

дедуктивная логика – формальная логика

сибиряк – пенсионер

3. Выявите логическую форму следующих высказываний:

* некоторые предметы не являются идеальными;

* Все хирурги являются врачами;

* ни один стуг не является тувелом;

4. Указать смысл и значение следующих имен:

* самая высокая гора на Алтае;

* ближайшая к Земле звезда;

* воспитатель Александра Македонского.

* основатель логики

* первый российский президент

* Автор произведения «Органон»

5. Подставляя вместо P и Q простые суждения, образуйте истинные высказывания:

* если P, то Q, следовательно, если не P, то не Q;

* если P, то Q, следовательно, если не Q, то не P;

* если P, то Q, следовательно, неверно, что P и не Q.

Перед вами три ложных утверждения. Укажите их.

1. 2 + 2 = 4

2. 3 + 6 = 11

3. 8 + 4 = 12

4. 13 - 7= 5

5. 5 + 4 = 9

1. На вопрос о количестве своих учеников Пифагор ответил:

Половина моих учеников изучает математику, четверть – музыку, а седьмая часть пребывает в молчании. Кроме того, есть еще три женщины.

Сколько всего учеников было у Пифагора?

8. Решите задачу:

Поезд № 648 отправляется из Барнаула в Томск в 15 ч.24 м. Через три часа другой поезд отправляется из Томска в Барнаул. Оба поезда идут с одной и той же скоростью.

Какой из них в момент их встречи будет находиться на меньшем расстоянии от Томска?

1. Решите задачу:

В нашем вузе организовали эстрадный концерт. Михаил играет на саксофоне и учится на экономическом факультете. Пианист учится на юридическом факультете. Ударника зовут Валерием. Андрей не пианист и не историк. Валерий учится не на философском факультете, а ударник – не на юридическом. Леонид играет не на гитаре.

На каких факультетах учатся студенты, и на каких инструментах они играют?

Тема 2. ПОНЯТИЕ КАК ФОРМА МЫШЛЕНИЯ

1. Понятие как форма мышления. Способы образования понятий. Объем и содержание понятий. Закон обратного отношения между объемом и содержанием понятий. Ограничение и обобщение понятий.

2. Виды понятий. Общие, единичные и пустые понятия. Регистрирующие и нерегистрирующие. Абстрактные и конкретные понятия, собирательные и разделительные, положительные и отрицательные, относительные и безотносительные.

3. Отношения между объемами понятий. Сравнимые и несравнимые. Совместимые и несовместимые. Отношения совместимости: полная совместимость, пересечение, подчинение. Отношения несовместимости: координация, контрарность, контрадикторность. Круговые схемы.

4. Определение, основные виды и правила определений. Особенности юридических дефиниций. Деление, основные виды и правила деления объема понятий. Виды и правила классификации. Естественная и вспомогательная классификации.

Упражнения

1. Выявить объем и содержание понятий:

* государство, общество, наука.

2. Определите виды следующих понятий:

* столица РФ, книга, спутник Земли.

3. Обобщить понятия:

* учебник по логике, конкретное понятие, майор, ложное суждение, студент 1 курса.

4. Ограничить понятия:

* государство, чемпион, космонавт, понятие, умозаключение.

5. Сформулировать контрарные и контрадикторные понятия:

* храбрость, взрослый, идеалист, грустный, добрый.

6. Найдите понятия, находящиеся в отношении пересечения:

* ученик 5 класса, депутат государственной думы, философ.

7. Изобразить в круговых схемах отношения между объемами понятий:

а) Наука, логика, философская наука, дедуктивная логика, формальная логика;

б) суждение, понятие, ложное суждение, форма мышления, пустое понятие, высказывание.

в) ученый, семейный человек, пенсионер, поэт, известный поэт, женщина;

г) врач, хирург, мужчина, сын, отец, лейтенант, офицер;

д) город, населенный пункт, город РФ, сибирский город, города Азии, большой город, большой сибирский город;

е) Мужчина, женщина, директор, юрист, известный юрист;

8. Сформулировать определения через родовое понятие и видовое отличие. Преобразовать эти определения в номинальные.

* школьник, демократия, человек, счастье, жизнь.

9. Определите вид и правильность следующих дефиниций:

· Логика – это наука, которую преподает мой дядя.

· Свидетель – это человек, являющийся свидетелем происшествия.

· Солнце – это большая звезда.

· Физика – это наука, которая не изучает общественные явления.

· Знание – сила;

· Криптография – наука о методах обеспечения конфиденциальности информации.

· Студент – это учащийся.

· Понятие – это форма мышления.

10. Подберите понятия, отношения между которыми соответствуют схеме:

А В С

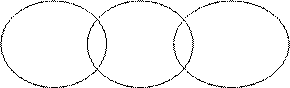
11. Дихотомически разделить объемы понятий:

* общество, наука, город.

12. Разделить объемы понятий по видоизменению признака:

* человек, логика, ученый.

Тема 3. СУЖДЕНИЕ КАК ФОРМА МЫШЛЕНИЯ

1. Суждение как форма мышления. Структура суждения. Виды простых суждений. Атрибутивные суждения, суждения об отношениях, суждения существования (экзистенциальные). Классификация простых категорических суждений по количеству и качеству. Распределенность терминов в суждениях.

2. Логические отношения между простыми категорическими суждениями (логический квадрат). Сравнимые и несравнимые суждения. Отношения полной совместимости, логического подчинения и частичной совместимости (субконтрарности). Отношения контрарности и контрадикторности.

3. Сложные суждения. Виды сложных суждений. Сложные соединительные суждения (конъюнктивные). Разделительные (дизъюнктивные), условные (импликативные), эквивалентные (двойная импликация). Условия истинности сложных суждений. Таблицы истинности.

4. Деление суждений по модальности. Понятие и виды модальности. Эпистемическая, деонтическая, алетическая. Алетическая модальность: Аподиктические, ассерторические и проблематические суждения. "Модальный" шестиугольник. Эпистемическая модальность суждений. Деонтическая модальность суждений.

5. Основные формально-логические законы. Закон тождества. Закон непротиворечия. Закон исключенного третьего. Закон достаточного основания.

Упражнения

1. Установите виды категорических суждений.

Некоторые понятия являются общими. Студенты являются учащимися. Ни один ученик не решил задачу. Большинство людей любят заниматься спортом.

2. Установить распределенность терминов в суждениях, изобразить отношения между терминами в круговых схемах.

Все выпускники университетов имеют высшее образование. Большинство войн являются захватническими. Логика не является описательной наукой.

3. Установить логические отношения между суждениями:

а) все студенты этой группы являются спортсменами. Некоторые студенты этой группы являются спортсменами;

б) всякое государство имеет законы. Некоторые государства не имеют законов;

в) некоторые вопросы являются уточняющими. Ни один вопрос не является уточняющим;

г) все граждане России имеют водительские удостоверения. Ни один гражданин России не имеет водительского удостоверения.

4. Сформулировать контрадикторные суждения по отношению к данным:

· Все бактерии вредны.

· Некоторые государства являются демократическими.

· Ни один гриб не является съедобным.

· Некоторые гипотезы не являются научными.

5. Установите вид сложного суждения, запишите суждения с помощью символов, используя логические связки.

Логика является наукой и изучает формы человеческого мышления. Каждый из нас знает книгу или хотя бы имя Льва Толстого. Неверно, что 5 делится на 2 или на 3. Если в этом человек по-настоящему силен, то ему покорятся другие, и вокруг него будет атмосфера доброго покоя. Если он при пожаре выпрыгнет из окна, то рискует получить либо ожоги, либо травмы, либо то и другое.

6. Постройте таблицы истинности для следующих формул:

а) (p & q) ⊃ p

б) ((p v q) ⊃ q) v p¯

в) ((p ⊃ q) v q) ⊃ q

7. Установить являются ли следующие суждения равносильными:

· Сын работает на заводе, а дочь учится в школе. Неверно, что сын не работает на заводе или дочь не учится в школе.

· Иван либо сын, либо внук Петра. Неверно, что Иван сын Петра тогда и только тогда, когда Иван является его внуком.

· Если слово ставится в начале предложения, то оно пишется с большой буквы. Неверно, что слово ставится в начале предложения и при этом не пишется с большой буквы.

8. Решите задачу, используя понятие равносильности высказываний.

В деле об убийстве имеются двое подозреваемых – Петр и Павел. Допросили четырех свидетелей. Показания первого таковы: "Я знаю только, что Петр не виноват".

Второй свидетель сказал: "Я знаю лишь, что Павел не виноват".

Третий свидетель: "Я знаю, что из первых двух показаний, по меньшей мере, одно истинно".

Четвертый: "Я знаю, что показания третьего свидетеля ложны".

Четвертый свидетель оказался прав. Кто же совершил преступление?

Тема 4. УМОЗАКЛЮЧЕНИЕ КАК ФОРМА МЫШЛЕНИЯ

1. Дедуктивные умозаключения. Непосредственные дедуктивные умозаключения. Превращение, обращение, противопоставление предикату, умозаключение по логическому квадрату.

2. Простой категорический силлогизм. Структура ПКС. Общие правила ПКС. Фигуры ПКС. Модусы фигур ПКС. Частные правила фигур ПКС. Преобразование модусов 2 и 3 фигуры ПКС в модусы 1 фигуры. Модусы фигур силлогизма в круговых схемах.

3. Дедуктивные умозаключения из сложных суждений: Чисто условные умозаключения. Условно-категорические умозаключения. Правильные и неправильные модусы условно-категорического умозаключения. Разделительно-категорические умозаключения. Утверждающе - отрицающий и отрицающее - утверждающий модусы разделительно-категорического умозаключения. Условно-разделительные умозаключения. Дилемма.

4. Сложные и сокращенные силлогизмы. Прогрессивный и регрессивный полисиллогизмы. Энтимемы, сориты и эпихейремы. Восстановление сокращенных силлогизмов в полные силлогизмы.

Упражнения

1. Произведите превращения следующих суждений:

* некоторые понятия являются конкретными;

* многие студенты не являются совершеннолетними;

* некоторые жители нашего города являются пенсионерами;

* все дороги являются ведущими в Рим;

* ни один присутствующий не является несовершеннолетним.

2. Обратить следующие суждения:

* все военнослужащие принимают присягу;

* некоторые барнаульцы обучаются в вузах;

* ни один невиновный не должен быть наказан;

* многие математики являются программистами;

* все законы природы являются объективными.

3. Сделайте вывод путем противопоставления предикату.

· Электрон имеет отрицательный заряд.

· Всякий товар имеет стоимость.

· Ни одна захватническая война не является справедливой.

· Некоторые гипотезы не являются обоснованными предположениями.

4. Определите фигуру, модус и правильность следующих силлогизмов:

а) Многие древние греки внесли большой вклад в развитие философии, а спартанцы – древние греки, следовательно, спартанцы внесли большой вклад в развитие философии;

б) все планеты – небесные тела. Луна – не планета. Значит, луна не является небесным телом;

в) Я – человек, а ты – не я, значит, ты – не человек.

г) Все люди с высшим образованием читали произведения Х.Л. Борхеса. Мой дядя – читал произведения Х.Л. Борхеса. Следовательно, он – человек с высшим образованием.

д) Лошадь погибает от одного грамма никотина, но я – не лошадь, следовательно, от одного грамма никотина я не погибну.

е) Все формы мышления являются способами рационального познания мира. Понятие – форма мышления. Следовательно, понятие – способ рационального познания мира.

5. Приведите примеры рассуждений по 1, 2 и 3 фигуре простого категорического силлогизма.

Сделайте полный разбор силлогизмов: укажите заключение и посылки, средний, меньший и больший термины. Определите фигуру, модус и корректность выводов при помощи общих и частных правил ПКС. Изобразите в круговых схемах отношения между терминами.

6. Правильно ли построены силлогизмы?

M i P М o Р P a M M a P

S a M M i SS o MM e S

S i P S i P S o P S o P

7. Модусы второй и третьей фигуры преобразовать в модусы первой фигуры.

8. Докажите, почему нельзя считать правильными:

а) по первой фигуре модусы АОО, АЕЕ, ОАО, ЕОО.

б) по третьей фигуре модусы ЕАЕ, АЕЕ, ААА.

9. Приведите пример вывода по правилу: следствие следствия есть следствие основания, то есть по следующей схеме:

(p ⊃ q) & (q ⊃ r)

p ⊃ r

Тема 5. ЛОГИКА ВЫСКАЗЫВАНИЙ

1. Логика высказываний в структуре современной формальной логики. Язык логики высказываний. Основные задачи и методы построения логики высказываний. Табличный метод. Правильно построенные формулы (ППФ). Таблицы истинности. Тождественно истинные, тождественно ложные и выполнимые формулы.

2. Понятие разрешимости логической системы. Равносильные формулы. Метод приведения к нормальным формам. Конъюнктивная нормальная форма (КНФ). Выявление законов логики при помощи приведения формул к КНФ. Дизъюнктивная нормальная форма (ДНФ). Тождественно ложные формулы. Совершенные нормальные формы. Сокращенные нормальные формы. Исчисление высказываний.

Упражнения

1. Установите с помощью табличного метода, являются ли следующие формулы законами логики:

______

а) p & p¯

б) (( p ⊃ q) & q) ⊃ q

в) (( p ⊃ q) & r) ⊃ (( p v r) ⊃ q)

г) ((p& q‾) ⊃ r) ≡ (p ⊃ (q ⊃ r))

д) ((p ⊃ q) & q) ⊃ ‾p

2. Запишите в символическом виде и проверьте с помощью таблиц наличие следования:

а) если бы Петров знал решение задачи, он рассказал бы его Смирнову и Николаеву. Если Смирнов не знает решения, то Петров его знает, а если Смирнов знает, то Николаев не знает. Значит, только Смирнов знает решение задачи;

б) если число делится на 2 и на 3, то оно делится и на 6. Значит, если число делится на 2, а на 6 не делится, то оно не делится и на 3;

в) если в какой-то точке пространства возникло переменное магнитное поле, то оно не стоит на месте, а со скоростью света распространяется во все стороны;

3. Следующие формулы привести к нормальным формам:

____

а) (p v q) ⊃ ((p &q) ⊃ p)

б) ((p ⊃ q) ⊃ (q ⊃ p)) ⊃ (p v q)

в) (p ≡ q) ⊃ (p &q)

г) ((p ⊃ q) & (q ⊃ r)) ⊃ (p &q)

д) ((p ⊃ q) ⊃ r) ⊃ p

е) (p v (q ⊃ r)) ⊃ p

ж) ((p ⊃ q) & (q ⊃ r)) ⊃ (p ⊃ r)

з) (p& q) ⊃ ((p ⊃ q) ⊃ q)

и) ((q ⊃ r) ⊃ q) ⊃ (r ⊃ p)

к) ((p & q) v (p ⊃ r)) ⊃ (q & r)

л) (p ≡ q) ⊃ p

4. Приведите к КНФ формулы:

а) (p& q) ⊃ ((p ⊃ q) ⊃ q)

б) (p ⊃ q) ⊃ ((p v r) ⊃ (q v r))

в) (p & (q v r)) ⊃ (‾p ⊃ ‾r)

_____

г) (‾p & ‾q) ⊃ (p v q)

д) (‾p v (q ⊃ r)) v ((p ⊃ ‾r) ⊃ (p ⊃ ‾q ))

е) (p ⊃ q) ⊃ (q v (‾p ⊃ r))

5. Приведите к ДНФ формулы:

а) (p ⊃ r) & (q v r)

_____ _________

б) (p v r) & ((q & r) v p)

в) (p ⊃ q) & (‾p v q)

_____

г) (p v r) & (p ⊃ q)

д) (p & q) & ((q ⊃ p) & p)

6. При помощи таблицы истинности установить являются ли равносильными формулы:

а) (p ⊃ q) и (‾q ⊃ ‾p)

б) (p ⊃ q) и (‾p v q)

в) (p ⊃ (q ⊃ r)) и ((p & q) ⊃ r)

г) (p & (q v r)) и ((p & q) v (p & r))

д) (p v (q & r)) и ((p v q) & (p v r))

7. Используя в качестве разрешающей процедуры процесс приведения к КНФ, решить задачу.

Три цеха договорились, что при утверждении проектов должны соблюдаться следующие условия:

· Если второй цех не участвует в утверждении проекта, то в нем не участвует и первый цех.

· Если второй цех принимает участие в утверждении проекта, то в нем принимают участие первый и третий цеха.

· Обязан ли при этих условиях третий цех принимать участие в утверждение проекта, когда в нем принимает участие первый цех?