Задания для самостоятельной работы. 1.2.1.1. Оценки вектора коэффициентов регрессии:
МНОЖЕСТВЕННАЯ РЕГРЕССИЯ
Расчетные формулы
1.2.1.1. Оценки вектора коэффициентов регрессии:
.
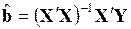1.2.1.2. Стандартная ошибка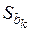 
k-го коэффициента регрессии, равная корню квадратному из соответствующего диагонального элемента ковариационной матрицы векторной оценки
,
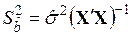где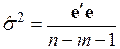 
рассчитывается по остаткам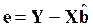 
1.2.1.3. Множественный индекс корреляции:
.
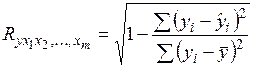1.2.1.4. Бета-коэффициенты:
.
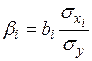1.2.1.5. Парные коэффициенты корреляции:
.
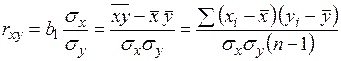1.2.1.6. Множественный коэффициент корреляции:
.
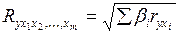1.2.1.7. Скорректированный коэффициент множественной детерминации:
.
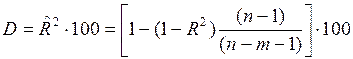1.2.1.8. Частный F-критерий:
.
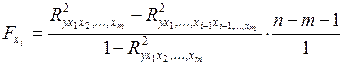1.2.1.9. Стандартную ошибку прогноза среднего
.
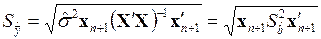1.2.10. Для проверки гипотезы о равенстве прогноза среднего значения заданной величине рассчитывается t-статистика:
.
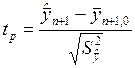Решение типовой задачи
Задание 1.2.2.1. Предприниматель желает сдать в аренду на один год принадлежащий ему отель*** «Блаженство жизни» (80 комнат), расположенный в престижной курортной зоне, обладающий собственным пляжем, общая площадь территории отеля составляет 3,42 кв.м.
Для того чтобы определить величину платы, которую он сможет установить за аренду своего отеля, предприниматель решил проанализировать ситуацию на соответствующей рыночной нише. Изучение объявлений, размещенных в газетах владельцами трехзвездных отелей, позволило ему сформировать небольшую базу данных, представленную в виде табл. 1.2.2.1.
На основе данных этой базы предприниматель решил построить модель множественной регрессии, отражающую зависимость величины годовой арендной платы от числа комнат, престижности района расположения отеля (1 – престижный район, 0 – нет), наличия у отеля собственного пляжа (1 – есть собственный пляж, 0 – нет), а также общей площади территории, принадлежащей отелю, и с помощью построенной модели определить примерный размер платы, которую он может получать за предоставление в аренду своего отеля.
На данный момент выбор предпринимателя колеблется между 162 тыс. руб. и 165 тыс. руб. Определите наиболее приемлемый размер арендной платы.
Т а б л и ц а 1.2.2.1
| Величина годовой платы за аренду отеля, тыс. руб. | Число комнат в отеле | Престижность района, в котором расположен отель | Наличие у отеля собственного пляжа | Общая площадь территории, принадлежащей отелю, кв. км. | |
| 1,00 | |||||
| 0,80 | |||||
| 1,20 | |||||
| 1,50 | |||||
| 1,40 | |||||
| 2,00 | |||||
| 2,50 | |||||
| 2,20 | |||||
| 2,70 | |||||
| 2,80 | |||||
| 3,00 | |||||
| 3,60 | |||||
| 3,50 | |||||
| 3,80 | |||||
| 3,60 | |||||
| 3,75 | |||||
| 4,10 | |||||
| 4,70 | |||||
| 4,25 | |||||
| 4,65 |
Решение с помощью табличного процессора Excel
1. Ввод исходных данных с включением дополнительной переменной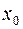 
, принимающей единственное значение, равное 1.
2. Расчет коэффициентов регрессии с использованием матричных функций Excel: ТРАНСП, МУМНОЖ, МОБР.
2.1. Нахождение обратной матрицы к матрице системы нормальных уравнений
| 0,4184 | 0,0040 | -0,0764 | -0,1095 | -0,1802 |
| 0,0040 | 0,0006 | 0,0007 | -0,0059 | -0,0136 |
| -0,0764 | 0,0007 | 0,2060 | -0,0330 | -0,0136 |
| -0,1095 | -0,0059 | -0,0330 | 0,2771 | 0,1144 |
| -0,1802 | -0,0136 | -0,0136 | 0,1144 | 0,3368 |
2.2. Получение вектора оценок коэффициентов регрессии
| 102,5677 |
| 0,1033 |
| -0,0194 |
| 2,6003 |
| 13,9271 |
Таким образом, построенная модель имеет следующий вид:
.
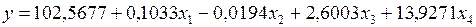3. Расчет стандартных ошибок коэффициентов регрессии
3.1. Проведение промежуточных расчетов, требуемых для расчета остаточной дисперсии, и оформление их в виде табл. 1.2.2.2.
Т а б л и ц а 1.2.2.2
 |  |  |
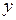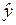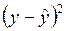| 121,6579 | 1,8012 | |
| 116,2916 | 1,6681 | |
| 124,9597 | 1,0821 | |
| 129,1573 | 0,7101 | |
| 125,1448 | 0,0210 | |
| 135,0698 | 1,1445 | |
| 142,0139 | 0,0002 | |
| 140,4556 | 0,2075 | |
| 144,8188 | 3,3080 | |
| 150,3611 | 0,1304 | |
| 153,1466 | 0,0215 | |
| 158,8831 | 0,7798 | |
| 161,6400 | 2,6895 | |
| 163,2372 | 0,0563 | |
| 163,0327 | 0,9357 | |
| 162,5408 | 29,8025 | |
| 172,5978 | 0,3574 | |
| 180,9347 | 0,8736 | |
| 176,7332 | 0,0712 | |
| 182,3235 | 0,1046 | |
| Сумма квадратов отклонений | 45,77 | |
| Остаточная дисперсия | 3,05 |
3.2. Получение стандартных ошибок
| 1,1299 |
| 0,0433 |
| 0,7927 |
| 0,9195 |
| 1,0137 |
4. Вычисление множественного коэффициента корреляции.
4.1. Проведение промежуточных расчетов и оформление их в виде табл. 1.2.2.3.
Т а б л и ц а 1.2.2.3
 |  |  |  |  |
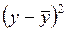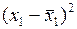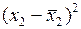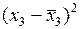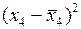| -1- | -2- | -3- | -4- | -5- |
| 742,56 | 0,30 | 0,16 | 3,43 | |
| 1242,56 | 0,20 | 0,36 | 4,21 | |
| 588,06 | 0,30 | 0,16 | 2,73 | |
| 410,06 | 0,20 | 0,16 | 1,83 | |
| 637,56 | 0,30 | 0,36 | 2,11 | |
| 264,06 | 0,20 | 0,36 | 0,73 |
О к о н ч а н и е т а б л. 1.2.2.3
| -1- | -2- | -3- | -4- | -5- |
| 68,06 | 0,30 | 0,36 | 0,12 | |
| 105,06 | 0,20 | 0,16 | 0,43 | |
| 52,56 | 0,20 | 0,36 | 0,02 | |
| 0,06 | 0,20 | 0,16 | 0,00 | |
| 7,56 | 0,20 | 0,16 | 0,02 | |
| 60,06 | 0,30 | 0,36 | 0,56 | |
| 95,06 | 0,30 | 0,16 | 0,42 | |
| 162,56 | 0,20 | 0,36 | 0,90 | |
| 189,06 | 0,30 | 0,16 | 0,56 | |
| 315,06 | 0,20 | 0,36 | 0,81 | |
| 473,06 | 0,20 | 0,16 | 1,56 | |
| 885,06 | 0,30 | 0,16 | 3,41 | |
| 715,56 | 0,30 | 0,16 | 1,95 | |
| 1008,06 | 0,20 | 0,16 | 3,23 | |
| Сумма квадратов отклонений | ||||
| 8021,75 | 4,95 | 4,80 | 29,03 | |
| Дисперсия | ||||
| 534,78 | 1151,33 | 0,33 | 0,32 | 1,94 |
| Среднее квадратическое отклонение | ||||
| 23,13 | 33,93 | 0,574 | 0,566 | 1,39 |
4.2. Расчет множественного коэффициента корреляции
.
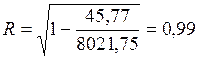Множественный коэффициент корреляции достаточно высокий, что свидетельствует о существенной зависимости величины арендной платы от включенных в модель факторов.
5. Расчет скорректированного множественного индекса корреляции
.
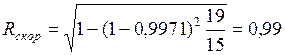6. Расчет бета-коэффициентов
,
,
,
.
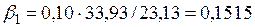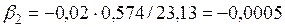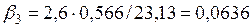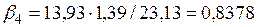Полученные значения бета-коэффициенты позволяют проранжировать факторы по степени их влияния на моделируемый показатель следующим образом:
1) общая площадь территории, принадлежащей отелю (в большей степени влияющий фактор);
2) число комнат в отеле;
3) наличие собственного пляжа;
4) престижность района, в котором расположен отель (в меньшей степени влияющий фактор).
7. Вычисление парных коэффициентов корреляции.
7.1. Проведение промежуточных расчетов и оформление результатов расчетов в виде табл. 1.2.2.4.
Т а б л и ц а 1.2.2.4
 |  |  |  |
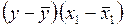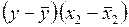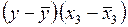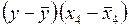| 1008,2500 | -14,9875 | -10,9000 | 50,4806 |
| 1304,2500 | 15,8625 | 21,1500 | 72,3506 |
| 776,0000 | -13,3375 | -9,7000 | 40,0731 |
| 648,0000 | 9,1125 | -8,1000 | 27,3881 |
| 808,0000 | -13,8875 | 15,1500 | 36,6756 |
| 276,2500 | 7,3125 | 9,7500 | 13,8531 |
| 140,2500 | -4,5375 | 4,9500 | 2,9081 |
| 174,2500 | 4,6125 | -4,1000 | 6,6881 |
| 123,2500 | 3,2625 | 4,3500 | 1,1056 |
| 0,5000 | 0,1125 | -0,1000 | 0,0131 |
| -5,5000 | -1,2375 | 1,1000 | 0,4056 |
| -15,5000 | 4,2625 | -4,6500 | 5,7931 |
| 126,7500 | 5,3625 | 3,9000 | 6,3131 |
| 165,7500 | -5,7375 | -7,6500 | 12,0806 |
| 178,7500 | 7,5625 | 5,5000 | 10,2781 |
| 230,7500 | -7,9875 | -10,6500 | 15,9306 |
| 826,5000 | -9,7875 | 8,7000 | 27,1331 |
| 1130,5000 | 16,3625 | 11,9000 | 54,9631 |
| 1551,5000 | 14,7125 | 10,7000 | 37,3831 |
| 1841,5000 | -14,2875 | 12,7000 | 57,0706 |
| Сумма произведений | |||
| 11290,00 | 2,75 | 54,00 | 478,89 |
7.2. Расчет парных коэффициентов корреляции
, 
,
, 
.
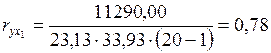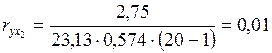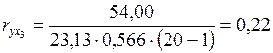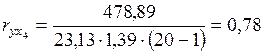8. Расчет дисперсионного отношения Фишера
.
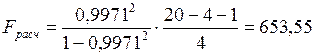Сравнение расчетного значения F-критерия с табличным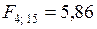 
для 95%-го уровня значимости (см. Приложение) позволяет сделать вывод об адекватности построенной модели.
9. Расчет t-статистик
, 
, 
,
, 
.
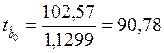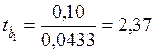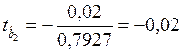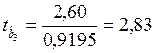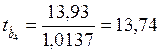Сравнение полученных t-статистик с табличным значением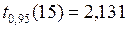 
(см. Приложение) подтверждает значимость таких коэффициентов регрессии, как 
, 
, 
, 
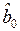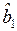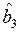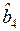, и незначимость коэффициента 
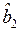. Скорее всего, это связано с тем, что престижность района, в котором расположен отель, в некоторой степени определяется наличием пляжа.
10. Построение с помощью пакета анализа линейного регрессионного уравнения, исключив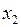 
(см. Вывод итогов 1.2.2.2).
| ВЫВОД ИТОГОВ 1.2.2.2 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,997143234 | |||||
| R-квадрат | 0,994294628 | |||||
| Нормированный R-квадрат | 0,993224871 | |||||
| Стандартная ошибка | 1,69128398 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 7975,983 | 2658,661 | 929,4583 | 3,739E-18 | ||
| Остаток | 45,76706 | 2,860442 | ||||
| Итого | 8021,75 | |||||
| Коэффиц-иенты | Стандартная ошибка | t-статис-тика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 102,5605062 | 1,056324 | 97,09187 | 1,34E-23 | 100,3212 | 104,7998 |
| Переменная X 1 | 0,103350894 | 0,041834 | 2,470506 | 0,025119 | 0,014667 | 0,192035 |
| Переменная X 2 | 2,597229942 | 0,881817 | 2,945315 | 0,009503 | 0,7278613 | 4,466599 |
| Переменная X 3 | 13,92581958 | 0,980218 | 14,20685 | 1,72E-10 | 11,84785 | 16,00379 |
Таким образом, пригодная для целей прогнозирования модель записывается в следующем виде:
.
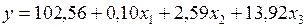11. Проверки обоснованности величины арендной платы, которую предприниматель желает назначить за свой отель
11.1. Расчет t-статистик по формуле (3.1.20)
; 
.
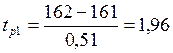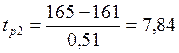11.2. Сравнение полученных t-статистик с табличным значением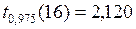 
(см. Приложение) свидетельствует о том, что первая величина арендной платы незначимо отличается от средней прогнозируемой величины, а вторая – значимо. Следовательно, предприниматель, назначая арендную плату 165 тыс. руб. в год рискует в большей степени не найти арендаторов своего отеля, чем при установлении размера платы в 162тыс. руб. или в 161 тыс. руб., поскольку 165 тыс. руб. существенно превышает средний сложившийся уровень арендной платы трехзвездных отелей в данной курортной зоне.
Задания для самостоятельной работы
Задание 1.2.3.1. В табл. 1.2.3.1 представлены данные о производительности труда, фондоотдаче и уровне рентабельности пятнадцати предприятий. Используя матричную форму метода наименьших квадратов, по данным этой таблицы рассчитайте:
1) коэффициенты регрессии;
2) стандартные ошибки коэффициентов регрессии;
3) множественный индекс корреляции;
4) скорректированное значение множественного коэффициента детерминации;
5) бетта-коэффициенты;
6) парные коэффициенты корреляции;
7) множественный коэффициент корреляции через бета-коэффициенты и парные коэффициенты корреляции;
8) дисперсионное отношение Фишера;
9) частные F-критерии для каждого фактора.
Т а б л и ц а 1.2.3.1
| № предприятия | Производительность труда, руб. | Фондоотдача, руб. | Уровень рентабельности, % |
| 1,08 | 20,1 | ||
| 1,05 | 12,9 | ||
| 0,99 | 18,0 | ||
| 1,02 | 11,7 | ||
| 0,98 | 17,9 | ||
| 1,04 | 16,8 | ||
| 1,03 | 15,6 | ||
| 1,10 | 14,3 | ||
| 1,03 | 18,1 | ||
| 0,89 | 17,8 | ||
| 0,78 | 13,0 | ||
| 0,99 | 14,2 | ||
| 1,43 | 24,2 | ||
| 1,03 | 20,0 | ||
| 1,05 | 19,3 |
Задание 1.2.3.2. Руководство крупной компании ЗАО «Надежная связь», предоставляющая услуги мобильной и стационарной телефонной связи, а также осуществляющая продажу телефонных аппаратов, планирует в следующем квартале расширить свой бизнес, освоив за счет прибыли компании новую рыночную нишу – предоставление Интернет-услуг в собственном Интернет-салоне. Получите прогнозные оценки прибыли компании в следующем квартале для того, чтобы у руководства сложилось представление о возможном размере финансового обеспечения этого бизнес-плана. Для построения прогнозной модели множественной регрессии воспользуйтесь данными табл. 1.2.3.2. Прогнозные оценки факторов, влияющие на прибыль компании, необходимо получить с помощью трендовых моделей.
Т а б л и ц а 1.2.3.2
| Квар-тал | Прибыль компании, тыс. руб. | Общее число абонентов компании | Выручка за мобильный трафик, тыс. руб. | Затраты на поддержание и обновление программного обеспечения, руб. | |
Задание 1.2.3.3. Экономисту-аналитику одной крупной компании было поручено указать обоснованный размер заработной платы руководителя будущего филиала этой компании. Ожидаемый объем среднемесячных продаж филиала составит 6500 тыс. у.е. Возраст сотрудника, который, как планируется, должен занять пост руководителя, – 45 лет, он имеет законченное высшее образование, а срок работы в должности директора другого филиала компании – 3 года. С целью решения поставленной задачи экономист-аналитик решил сначала изучить опыт других компаний, собрав сведения представленные в табл. 1.2.3.3, в которой за 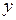обозначена среднемесячная заработная плата руководителей, у.е.; за 
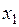– возраст, лет; за 
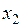– образование (0 – нет высшего образование, 1 – незаконченное высшее, 2 – высшее); за 
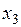– срок работы в должности руководителя, лет; за 
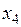– годовой объем продаж компании, тыс. у.е.
Т а б л и ц а 1.2.3.3
| Компания | 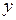| 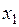| 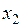| 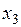| 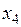| Ком-пания | | | | | |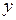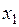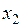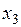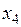
| 1 652 | 12 949 | ||||||||||
| 1 948 | 1 227 | 5 061 | |||||||||
| 1 735 | 1 712 | 1 929 | |||||||||
| 1 681 | 1 488 | 2 643 | |||||||||
| 1 461 | 5 673 | 1 084 | |||||||||
| 1 117 | 1 752 | 5 137 | |||||||||
| 1 475 | 2 497 | ||||||||||
| 2 094 | 10 818 | 2 097 | |||||||||
| 2 686 | 2 342 | ||||||||||
| 3 409 | 14 021 | ||||||||||
| 2 244 | 4 451 | ||||||||||
| 1 539 | 1 911 | ||||||||||
| 2 833 | 11 663 | 1 554 | 1 435 | ||||||||
| 2 366 | 1 314 | ||||||||||
| 1 856 | 4 864 | 2 301 |
Постройте модель множественной регрессии, отражающую зависимость среднемесячной зарплаты от указанных факторов, и оцените ее качество. Используя построенную модель, осуществите расчет заработной платы руководителя будущего филиала компании.
Задание 1.2.3.4. Исследуйте зависимость урожайности зерновых культур (ц/га) от следующих факторов сельскохозяйственного производства:
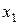– число тракторов на 100 га;
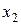– число зерноуборочных комбайнов на 100 га;
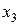– число орудий поверхностной обработки почвы на 100 га;
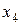– количество удобрений, расходуемых на гектар (т/га);
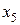– количество химических средств защиты растений, расходуемых на гектар (ц/га).
Исходные данные для 20 районов области приведены в табл. 1.2.3.4.
Т а б л и ц а 1.2.3.4
| Районы области |  | | | | | |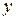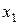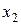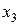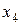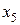
| -1- | -2- | -3- | -4- | -5- | -6- | -7- |
| 9,7 | 1,59 | 0,26 | 2,05 | 0,32 | 0,14 | |
| 8,4 | 0,34 | 0,28 | 0,46 | 0,59 | 0,66 | |
| 9,0 | 2,53 | 0,31 | 2,46 | 0,30 | 0,31 | |
| 9,9 | 4,63 | 0,40 | 6,44 | 0,43 | 0,59 | |
| 9,6 | 2,16 | 0,26 | 2,16 | 0,39 | 0,16 | |
| 8,6 | 2,16 | 0,30 | 2,69 | 0,32 | 0,17 |
О к о н ч а н и е т а б л. 1.2.3.4
| -1- | -2- | -3- | -4- | -5- | -6- | -7- |
| 12,5 | 0,68 | 0,29 | 0,73 | 0,42 | 0,23 | |
| 7,6 | 0,35 | 0,26 | 0,42 | 0,21 | 0,08 | |
| 6,9 | 0,52 | 0,24 | 0,49 | 0,20 | 0,08 | |
| 13,5 | 3,42 | 0,31 | 3,02 | 1,37 | 0,73 | |
| 9,7 | 1,78 | 0,30 | 3,19 | 0,73 | 0,17 | |
| 10,7 | 2,40 | 0,32 | 3,30 | 0,25 | 0,14 | |
| 12,1 | 9,36 | 0,40 | 11,51 | 0,39 | 0,38 | |
| 9,7 | 1,72 | 0,28 | 2,26 | 0,82 | 0,17 | |
| 7,0 | 0,59 | 0,29 | 0,60 | 0,13 | 0,35 | |
| 7,2 | 0,28 | 0,26 | 0,30 | 0,09 | 0,15 | |
| 8,2 | 1,64 | 0,29 | 1,44 | 0,20 | 0,08 | |
| 8,4 | 0,09 | 0,22 | 0,05 | 0,43 | 0,20 | |
| 13,1 | 0,08 | 0,25 | 0,03 | 0,73 | 0,20 | |
| 8,7 | 1,36 | 0,26 | 0,17 | 0,99 | 0,42 |
Задание 1.2.3.5. Торговое предприятие «Альянс» имеет сеть, состоящую из 12 магазинов, информация о деятельности которых представлена в табл. 1.2.3.5. Постройте:
1) диаграммы рассеяния годового товарооборота ( 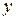) в зависимости от торговой площади ( 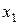) и среднего числа посетителей в день ( 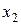) и определите форму связи между результирующим показателем и каждым из этих факторов;
2) двухфакторное регрессионное уравнение, отражающее зависимость переменной 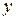от соответствующих факторов 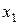и .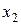
Оцените:
1) качество построенного уравнения;
2) частные коэффициенты эластичности годового товарооборота от торговой площади и от среднего числа посетителей.
Т а б л и ц а 1.2.3.5
| № мага-зина | Годовой товарооборот, млн. руб. | Торговая площадь, тыс. кв.м. | Среднее число посетителей в день, тыс. чел. |
| 19,76 | 0,24 | 8,25 | |
| 38,09 | 0,31 | 10,24 | |
| 40,95 | 0,55 | 9,31 | |
| 41,08 | 0,48 | 11,01 | |
| 56,29 | 0,78 | 8,54 | |
| 68,51 | 0,98 | 7,51 | |
| 75,01 | 0,94 | 12,36 | |
| 89,05 | 1,21 | 10,81 | |
| 91,13 | 1,29 | 9,89 | |
| 91,26 | 1,12 | 13,72 | |
| 99,84 | 1,29 | 12,27 | |
| 108,55 | 1,49 | 13,92 |