Интервальные оценки коэффициентов регрессии

По аналогии с парной регрессией после опре­деления точечных оценок 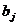коэффициентов 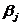- (j =0,1,…,m) теоретического уравнения регрессии могут быть рассчитаны ин­тервальные оценки указанных коэффициентов. Для построения интервальной оценки коэффициента 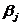строится 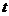-статистика

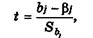(6.26)

имеющая распределение Стюдента с числом степеней свободы v= n — т — 1 (n— объем выборки, т - количество объясняю­щих переменных в модели)

Пусть необходимо построить 100(1 — 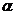)%-й доверительный интервал для коэффициента 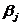Тогда по таблице критических точек распределения Стьюдента по требуемому уровню значи­мости а и числу степеней свободы 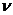находят критическую точку Удовлетворяющую условию

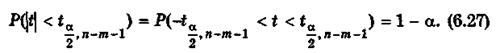
Подставляя (6.26) в (6.27), получаем

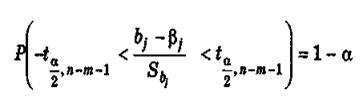
или после преобразования

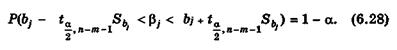
Напомним, что 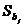рассчитывается по формуле

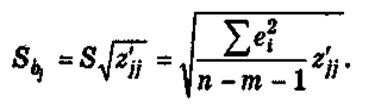
Таким образом, доверительный интервал, накрывающий с надежностью (1 – 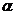) неизвестное значение параметра 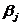, опре­деляется неравенством

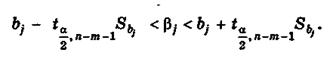
Отметим, что по аналогии с парной регрессией (может быть построена интервальная оценки для среднего значения предсказания:

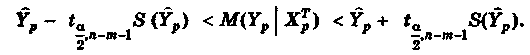
В матричной форме это неравенство имеет вид:

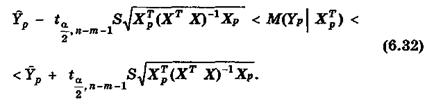
17)Коэффициент детерминации R². Отличие скорректированного коэффициента детерминации от обычного.

После проверки значимости каждого коэффициента регрес­сии обычно проверяется общее качество уравнения регрессии. Для этой цели, как и в случае парной регрессии, используется

коэффициент детерминации R , который в общем случае рас­считывается по формуле

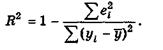
Как отмеча­лось, в общем случае 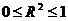. Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение У. Поэтому естественно желание построить регрессию с наи­большим R².

Для множественной регрессии коэффициент детерминации является неубывающей функцией числа объясняющих пере­менных. Добавление новой объясняющей переменной никогда не уменьшает значение R². Действительно, каждая следующая объясняющая переменная может лишь дополнить, но никак не сократить информацию, объясняющую поведение зависимой переменной. Это уменьшает (в худшем случае не увеличивает) область неопределенности в поведении У.

Иногда при расчете коэффициента детерминации для полу­чения несмещенных оценок в числителе и знаменателе вычи­таемой из единицы дроби делается поправка на число степеней свободы. Вводится так называемый скорректированный (ис­правленный) коэффициент детерминации:

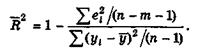(6.35)

Можно заметить, что 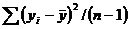является несмещенной оценкой общей дисперсии — дисперсии отклонений значений переменной У от 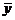. При этом число ее степеней сво­боды равно (n — 1). Одна степень свободы теряется при вычис­лении .

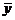В свою очередь 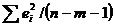является несмещенной оцен­кой остаточной дисперсии — дисперсии случайных отклонений (отклонений точек наблюдений от линии регрессии). Ее число степеней свободы равно (n - m -1). Потеря (m + 1) степени свобо­ды связана с необходимостью решения системы (m + 1) линейно­го уравнения при определении коэффициентов эмпирического уравнения регрессии. Попутно заметим, что несмещенная оцен­ка объясненной дисперсии (дисперсии отклонений точек на ли­нии регрессии от 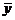) имеет число степеней свободы, равное разно­сти степеней свободы общей дисперсии и остаточной дисперсии (n — 1) — (n- m -1) = m.

Соотношение (6.35) может быть представлено в следую­щем виде:

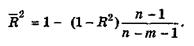(6.36)

Из (6.36) очевидно, что 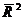< R² для m > 1. С ростом значения m скорректированный коэффициент детерминации 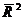рас­тет медленнее, чем (обычный) коэффициент детерминации R². Другими словами, он корректируется в сторону уменьшения с ростом числа объясняющих переменных. Нетрудно заметить, что 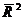= R² только при R² = 1. 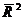может принимать отрица­тельные значения (например, при R² = 0).

Доказано, что R увеличивается при добавлении новой объ­ясняющей переменной тогда и только тогда, когда t-статистика для этой переменной по модулю больше единицы. Поэтому до­бавление в модель новых объясняющих переменных осуществ­ляется до тех пор, пока растет скорректированный коэффици­ент детерминации.

Обычно приводятся данные как по R², так и по 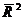, яв­ляющиеся суммарными мерами общего качества уравнения регрессии. Однако не следует абсолютизировать значимость коэффициентов детерминации. Существует достаточно приме­ров неправильно специфицированных моделей, имеющих высо­кие коэффициенты детерминации (обсудим данную ситуацию позже). Поэтому коэффициент детерминации в настоящее вре­мя рассматривается лишь как один из ряда показателей, кото­рый нужно проанализировать, чтобы уточнить строящуюся модель.

18)Анализ статистической значимости коэффициента детерминации R².

на практике чаще вместо указанной гипотезы про­веряют тесно связанную с ней гипотезу о статистической значи­мости коэффициента детерминации R²:

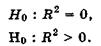
Для проверки данной гипотезы используется следующая F-статистика:

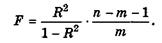(6.38)

Величина F при выполнении предпосылок МНК и при спра­ведливости Но имеет распределение Фишера, аналогичное рас­пределению F-статистики (6.37). Действительно, разделив чис­литель и знаменатель дроби в (6.37) на общую сумму квадратов отклонений 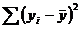, мы получим формулу(6.38);

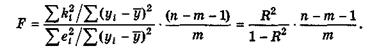
Из (6.38) очевидно, что показатели F и R² равны или не равны нулю одновременно. Если F = 0, то R² = 0, и линия регрессии Y = 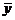является наилучшей по МНК, и, следова­тельно, величина Y линейно не зависит от 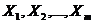.Для проверки нулевой гипотезы 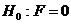при заданном уровне значимости 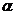по таблицам критических точек распределения Фишера находится критическое значение 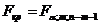. Нуле­вая гипотеза отклоняется, если F_набл > F_кр, Это равносильно тому, что R² > 0, т.е. R статистически значим.

Анализ статистики F позволяет сделать вывод о том, что для принятия гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии коэффициент детермина­ции R² не должен существенно отличаться от нуля. Его критическое значение уменьшается при росте числа наблюдений и может стать сколь угодно малым.

Пусть, например, при оценке регрессии с двумя объясняющими переменными по 30 наблюдениям R² = 0,65. Тогда F_набл= .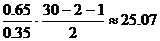

По таблицам критических точек распределения Фишера найдем . 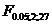=3,36; 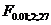= 5,49. = 25,07 > F_кр как при 5% -м, так и при 1%-м уровне значимости, то нулевая гипотеза в обоих случаях отклоняется.

Если в той же ситуации 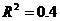, то 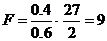. Предположение о незначимости связи отвергается и здесь.

Отметим, что в случае парной регрессии проверка нулевой гипо­тезы для F-статистики равносильна проверке нулевой гипотезы для t-статистики 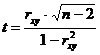коэффициента корреляции.

В этом случае F-статистика равна квадрату t-статистики. Самостоятельную значимость коэффициент R² приобретает в случае множественной линейной регрессии.