Интервальные оценки коэффициентов линейного уравнения регрессии.

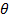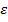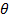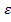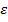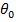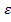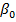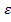Интервальной оценкой называется оценка, определяющая числовой интервал ( - , + ), >0, содержащий оцениваемый параметр , т.е. b- < <b+ . Доверительным интервалом называют интервал 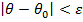, в котором с заданной вероятностью 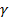заключен неизвестный параметр 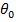, а сама вероятность 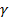называется доверительной вероятностью или надежностью, т.е. R( 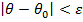)=1

Уровнем значимости 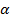называется вероятность Р( 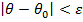)= 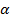, причем 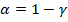, т.к. из предпосылок МНК 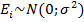, кэофициенты b₀ и b₁ также имеют нормальное распределение 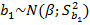.Тогда 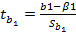имеет распределение Cтьюдента с числом степени свободы v=n-2. По заданной дов-ой вероятности 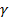можно найти интервал 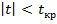, внутри которого находится значение t с вероятностью 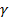P( )=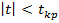

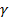
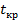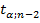= ( по таблице двухсторонних квантилей распределения Стьюдента)

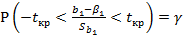Т.о. ; P(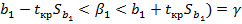

(доверительный интервал для коэффициента b₁ парной линейной регрессии с доверительной вероятностью )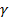

8. Доверительные интервалы для зависимой переменной в уравнении регрессии.

Базовой предпосылкой МНК является предположение о нормальном распределении отклонений 𝜀𝑖 с нулевым математическим ожиданием и постоянной дисперсией 𝜎2, которое является теоретически и практически обоснованным: 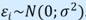Согласно модельному уравнению линейной парной регрессии 𝑦𝑖 = 𝛽0 +𝛽1𝑥𝑖 +𝜀𝑖, коэффициенты 𝑏0 и 𝑏1 через 𝑦𝑖 являются линейными комбинациями 𝜀𝑖. Следовательно, 𝑏0 и 𝑏1 также имеют нормальное распределение: 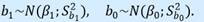Тогда случайные величины 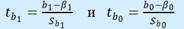имеют распределение Стьюдента с числом степеней свободы 𝜈 = 𝑛 −2. По заданной доверительной вероятности γ можно найти интервал: −𝑡кр < 𝑡 < 𝑡кр или 𝑡 < 𝑡кр внутри которого находятся значения 𝑡 с вероятностью γ: 𝑃(|𝑡| < 𝑡кр) = 𝛾. (2.30) Критическое значение 𝑡кр при доверительной вероятности 𝛾 = 1−𝛼 находятся по таблицам двусторонних квантилей распределения Стьюдента 𝑡кр = 𝑡𝛼;𝑛−2. Таким образом: 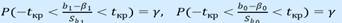После преобразований получим: 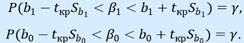Доверительные интервалы для коэффициентов парной линейной регрессии с доверительной вероятностью 𝛾 = 1−𝛼 имеют вид: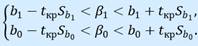

9. Проверка общего качества уравнения регрессии. Коэффициент детерминации R².

Суммарной мерой общего качества уравнения регрессии (соответствия статистическим данным) является коэффициент детерминации R². Пусть уравнение регрессии имеет вид: 𝑦𝑖 = 𝑏0 +𝑏1𝑥𝑖, тогда рассчитанные по модели значения 𝑦 𝑖 для наблюдаемых значений 𝑥𝑖 равны 𝑦 𝑖=𝑏0 +𝑏1𝑥𝑖. Наблюдаемые значения 𝑦𝑖 отличаются от рассчитанных по модели значений 𝑦 𝑖 на величину 𝑒𝑖: 𝑦𝑖 = 𝑦 𝑖 +𝑒𝑖. Представим это равенство в виде 𝑦𝑖 −𝑦 = (𝑦 𝑖 −𝑦 )+𝑒𝑖. Введем обозначения: 𝑄𝑦 = (𝑦𝑖 −𝑦 )2 = 𝑦𝑖2 −𝑛(𝑦 )2;𝑛 𝑖=1 𝑛 𝑖=1 𝑄𝑅 = (𝑦 𝑖 −𝑦 )2;𝑛 𝑖=1 𝑄𝑒 = 𝑒𝑖2, 𝑛 𝑖=1 (2.17) тогда 𝑄𝑦 = 𝑄𝑅 +𝑄𝑒. Здесь: 𝑄𝑦- полная сумма квадратов отклонений: мера разброса наблюдаемых значений результирующего признака Y относительно среднего значения 𝑦 . 𝑄��- объясненная сумма квадратов отклонений: мера разброса, объясненного уравнением регрессии. 𝑄𝑒- остаточная (необъясненная) сумма квадратов отклонений: мера разброса не объясненного уравнением регрессии.

Коэффициент детерминации определяется как доля разброса переменной Y, объясняемая регрессией Y на X: 𝑅² = 𝑄𝑅 𝑄𝑦 . (2.18) Так как 𝑄𝑅 = 𝑄𝑦 −𝑄𝑒, то 𝑅2 = 1− 𝑄𝑒 𝑄 𝑦 . Вывод: Коэффициент детерминации 𝑅2 изменяется в пределах: 0 ≤ 𝑅2 ≤ 1. Если 𝑄𝑒 = 0, то 𝑅2 = 1 и все наблюдаемые значения 𝑦𝑖 лежат на линии регрессии, то есть между Y и Х имеется строгая функциональная зависимость. Если 𝑅² = 0 , то регрессия ничего не объясняет. Следовательно, чем ближе 𝑅² к 1, тем лучше уравнение регрессии объясняет наблюдаемые значения.