Отражение региональных связей при анализе функционирования экономических систем. Статическая модель межрегионального МОБа. Динамические модели МОБа

Межрегиональные межотраслевые модели явл-ся эффек-м инструментом анализа и планирования. Они синтезируют региональные межотраслевые модели и представляют пространственную развертку сводных межотраслевых моделей. В дальнейшем: территория представлена m регионами, r – регион-производитель, s-регион-потребитель. В регионах n отраслей, i–отрасль-производитель, j–отрасль-потребитель. Предпосылки для модели те же, как и при статической МОБ. Возможны три схемы объединения региональных межотраслевых моделей: 1. сводят все региональные модели в "точечную" модель народного хозяйства, совпадающую с основным вариантом модели межотраслевого баланса: региональные величины производства, конечного испол-ния продукции и ресурсов складывают, коэфф-ты прямых затрат сводной модели рассчит-ся как средневзвешенные величины из региональных; 2. сохраняют часть элементов региональных моделей (объем производства, коэфф-ты затрат), другую часть суммирует (внутрирегиональное конечное исполь-ние продукции, региональные ресурсы), третью - исключает из рассмотрения (межрегион-е поставки продукции). 3. Сохраняет все условия и информацию региональных моделей и, кроме того, включает условия согласования межрегиональных связей. Межрег-й МОБ имеет вид шахматной таблицы. В подлежащем- регионы-производители, в сказуемом — регионы-потребители. Каждый блок таблицы содержит межотр-е потоки текущего производственного потребления и конечного использования продукции. 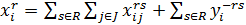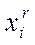Соотношения показателей по горизонтали: , где — объем произ-ва продукции i-й отрасли в рег. r; 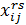— объем продукции i-й отрасли, пост-мой из rв s для произ-ва продукции j-й отрасли; 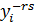— объем продукции i-й отрасли, постав-мой из rв s для конечного использования. При объединении условий региональных межотраслевых балансов по 2ой и 3ей схеме возникает избыточное числопеременных. Необходимо устранить множественность выбора межотраслевых и межрегиональных связей. Матем. модель межрег-го баланса - система алгебраических уравнений, имеющая единственное решение. Устранение всех степеней свободы достигается посредством введения дополнительных параметров, фиксирующих структуру некоторых территориальных пропорций.

Основное предположение: региональная структура потребления продукции устойчива.

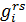– доля продукции i-й отрасли, произведенной регионом r, в производственном и непроизводственном потреблении региона s: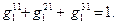

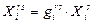
рег.-потребит	Регион 1	Регион 2	Конечное использование	Вал. Прод-я
		Отрасли	Отрасли
Рег-произв					Рег 1	Рег 2
Рег 1	Отрасли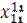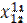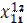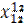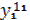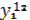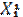
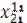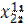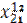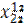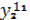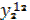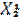Рег 2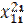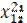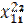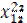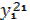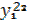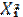

,

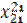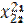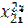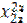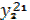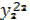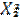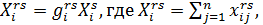
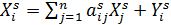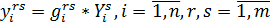
С учетом вышеизложенных формул получится модель межрегионального МОБа:

В векторно-матричной записи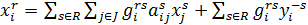

В матричной записи выглядит так X=GAX+GY, где G = (Grs), r, sÎR, а каждый блок Grs — диагональная матрица из коэффициентов 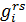, А — блочно-диагональная матрица из матриц Аr; векторы X, Y — композиции региональных векторов X^r, Y^s. Строятся след. образом:

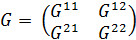
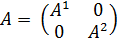
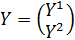X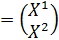

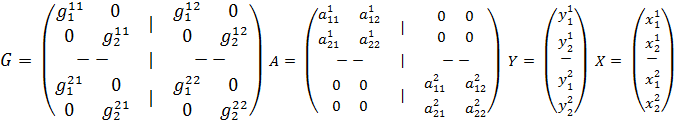
Системы уравнений и можно выразить через обратные матрицы: X=(G^-1 – A)^-1Y

По своему эконом-му содержанию G = (G^-1 – A)^-1это межрегиональная матрица коэффициентов полных затрат продукции. Каждый элемент этой матрицы характеризует объем производства продукции i-й отрасли в r-м регионе, необходимый для конечного использования единицы продукции j-и отрасли в s-м регионе.

Заполняем таблицу матрицами, элементы кот равны:

, .

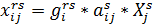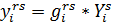Простейшая модель МОБ в векторной форме: X=AX+Y

X=(X₁, X₂,.. ,X_n)^T – вектор-столбец валовой продукции отраслей

Y=(Y₁, Y₂,.. ,Y_n)^T – вектор-столбец конечного спроса на продукцию отраслей

A=( a_ij ) – матрица коэффициентов прямых материальных затрат

Матрица A продуктивна, если существует неотрицательный вектор X⁰ такой, что выполняется матричное неравенство X⁰>A· X⁰

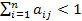, для всех j=1,2,..,n.

Если А известна и при этом продуктивна, вектор – столбец Y экзогенно задан, и Y≥0

X=(E-A)^-1·Y

Коэффициенты матрицы В=( b_ij )=(E-A)^-1, где Е – единичная матрица размерности n×n называются коэффициентами полных материальных затрат.