Задания для самостоятельной работы. 1) Исследуйте возможность применения техники доступа МДПН/ОC для системы кабельного телевидения с наибольшим удалением пользователя от головного окончания X

1) Исследуйте возможность применения техники доступа МДПН/ОC для системы кабельного телевидения с наибольшим удалением пользователя от головного окончания X км. Размер кадров возьмите из согласно варианту из таблицы заданий. Какова максимальная скорость передачи в канале, если а должно быть не больше 0.1? Примите время распространения сигнала равным Y мкс/км. (см. Данные в таблице). Найдите максимальное число пользователей при интенсивности передачи сигнала от одного пользователя в 1 кадр за Z c (см. Данные в таблице).

2) Разработайте программу, моделирующую работу сети типа МДПН/ОС

3) Проведите качественный анализ полученных результатов

Таблица исходных данных

№ Варианта	Удаление пользователя от головной части	Длина кадра	Время распространения сигнала	Интенсивность передачи
			4.5
			7.5
			10.5
			9.5

Содержание отчета

1. Титульный лист.

2. Наименование и цель работы.

3. Отчет по заданию.

4. Выводы по работе

Лабораторная работа № 7

Программирование алгоритмов маршрутизации

Цель и порядок выполнения работы

Цель работы - ознакомление с управлением процессами маршрутизации пакетов, передаваемых через сеть. Изучение теории выбора кратчайших путей и ее методов.

Порядок выполнения работы:

- ознакомиться с описанием лабораторной работы;

- написать программу в соответствии с вариантом, ввести программу, отладить и решить ее на ЭВМ;

- оформить отчет.

Общие сведения

Теоретическую основу современных информационных сетей определяет Базовая эталонная модель взаимодействия открытых систем (OSI - Open Systems Interconnection) Международной организации стандартов (ISO - International Standards Organization). Она описана стандартом 7498. Модель является международным стандартом для передачи данных. Согласно эталонной модели взаимодействия OSI выделяются семь уровней, образующих область взаимодействия открытых систем (табл.1).

Таблица1. Функции уровней модели взаимодействия открытых систем

Уровень	Функции
7. Прикладной	Интерфейс с прикладными процессами
6. Представительный	Согласование представления и интерпретация передаваемых данных
5. Сеансовый	Поддержка диалога между удаленными процессами; обеспечение соединения и разъединения этих процессов; реализация обмена данными между ними
4. Транспортный	Обеспечение сквозного обмена данными между системами
3. Сетевой	Маршрутизация; сегментирование и объединение блоков данных; управление потоками данных; обнаружение ошибок и сообщение о них
2. Канальный	Управление каналом передачи данных; формирование кадров; управление доступом к среде передачи; передача данных по каналу; обнаружение ошибок в канале и их коррекция
1. Физический	Физический интерфейс с каналом передачи данных; битовые протоколы модуляции и линейного кодирования

Основная идея этой модели заключается в том, что каждому уровню отводится конкретная роль. Благодаря этому, общая задача передачи данных расщепляется на отдельные конкретные задачи. Функции уровня, в зависимости от его номера, могут выполняться программными, аппаратными либо программно-аппаратными средствами. Как правило, реализация функций высших уровней носит программный характер, функции канального и сетевого уровней могут быть исполнены как программными, так и аппаратными средствами. Физический уровень обычно выполняется в аппаратном виде.

Каждый уровень определяется группой стандартов, которые включают в себя две спецификации: протокол и обеспечиваемый для вышестоящего уровня сервис. Под протоколом подразумевается набор правил и форматов, определяющих взаимодействие объектов одного уровня модели.

Наиболее близким к пользователю является прикладной уровень. Его главная задача - предоставить уже переработанную (принятую) информацию. С этим обычно справляется системное и пользовательское прикладное программное обеспечение, например, терминальная программа. Прикладные программы взаимодействующих пользователей должны работать с одинаковыми кодовыми таблицами. Количество предоставленных в коде знаков зависит от числа битов, используемых в коде, т.е. от основания кода.

В большинстве сетей с коммутацией пакетов, находящихся в эксплуатации в настоящее время, для выполнения функций по выбору маршрутов на сетевом уровне применяется в различных формах выбор кратчайших путей. В некоторых сетях выбор маршрутов выполняется централизованно, т.е. установление путей между узлами источника и получателя осуществляется в центре управления сетью, а затем полученная в результате информация распределяется по всем узлам сети. В других сетях применяется децентрализованный выбор маршрутов, и в этом случае каждый узел обменивается информацией о стоимости и маршрутах со своими соседними узлами в ходе взаимодействия с ними до тех пор, пока в узлах не сформируются таблицы маршрутов с необходимыми данными о кратчайших путях.

Рассмотрим алгоритмы Дейкстры и Флойда для выполнения вычислений кратчайшего пути. Оба эти алгоритма или их версии применяются в различных действующих сетях для выполнения функций выбора маршрутов.

Алгоритм Дейкстры.

Переходим к описанию алгоритма Дейкстры. Рассмотрим сеть на рис.1

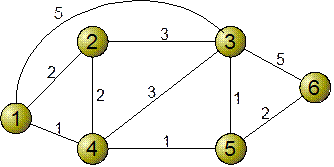
Рис.1 Пример сети

Числа, проставленные у каждой линии, указывают ее стоимость (ради простоты стоимость в обоих направлениях предполагается одинаковой; однако в более общем случае стоимость передачи в разных направлениях может и различаться). Алгоритм Дейкстры позволяет найти кратчайшие пути от источника ко всем другим узлам. Для этого требуется знание глобальной структуры, т.е. списка всех узлов сети и их взаимосвязей, а также стоимости каждой линии. Таким образом, алгоритм Дейкстры служит для централизованных вычислений с полной информацией о структуре, имеющейся на центральной базе данных. В примере на рис.1 целью является нахождение кратчайшего пути от узла 1, являющегося источником, ко всем остальным узлам сети. Алгоритм решает эту задачу поэтапно, строя дерево кратчайших путей с корнем в узле-источнике (в данном примере в узле 1), пока будет охвачен самый удаленный узел. На k-м шаге вычисляются кратчайшие пути к k-узлам, ближайшим к источнику. Они определяются как находящиеся внутри множества N. Опишем алгоритм неформально.

Обозначим через D(v) расстояние (сумму весов каналов вдоль данного пути) от источника 1 до узла v. Пусть l(i,j) - заданная стоимость пути между узлами i и j. Алгоритм состоит из двух частей: начального шага и итераций, повторяющихся до завершения алгоритма.

1. Начальный шаг. Устанавливаем N={1}. Для каждого узла v, не принадлежащего множеству N, устанавливаем D(v)=l(1,v). (Расстояние до узлов, не соединенных с узлом 1, принимаем равным ¥; практически можно принять любое число, большее максимальной стоимости или расстояния.)

2. Каждый последующий шаг. Находим не принадлежащий множеству N узел w, для которого D(w) минимально и включаем w в множество N. Затем обновляем значения D(v) для всех остальных узлов, не принадлежащих N путем вычисления

.

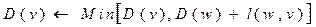Шаг 2 повторяется, пока в множество N не войдут все узлы.

Применение алгоритма Дейкстры к сети на рис.1 иллюстрируется последовательными шагами, указанными в таблице1.1. Полужирным курсивом в столбцах обозначены минимальные значения D(w) на каждом шаге (при равных расстояниях выбор производится случайным образом). После каждого шага соответствующий узел w добавляется к N. Затем величины D(v) обновляются. Например, после начального шага во время шага 1 к множеству N добавляется узел 4, имеющий минимальное значение D(4)=1. На шаге 2 в N включается узел 5 при D(5)=2, и т.д. После шага 5 все узлы оказываются включенными в множество N, и алгоритм завершается.

Таблица1.1 Применение алгоритма Дейкстры к сети рис.1

Шаг	N	D(2)	D(3)	D(4)	D(5)	D(6)
Начальный	{1}				¥	¥
	{1,4}					¥
	{1,4,5}
	{1,2,4,5}
	{1,2,3,4,5}
	{1,2,3,4,5,6}

По мере работы алгоритма, приводящей к результатам, показанным в табл.1.1, в то же самое время строится дерево кратчайших путей с корнем в узле 1: при включении узла во множество N он соединяется с соответствующим узлом, уже принадлежащим N. Результирующее дерево для сети на рис.1 показано на рис.2а.

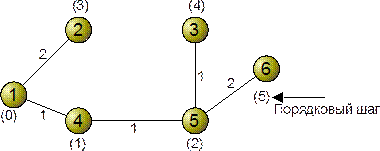
а

Получатель Следующий шаг

2 2

3 4

4 4

5 4

6 4

б

Рис.2. Применение алгоритма Дейкстры к рис.1;

источник-узел 1: (а) построение дерева кратчайших путей,

(б) таблицы маршрутов, узел 1.

Цифры в скобках у каждого узла указывают шаг, на котором этот узел был включен в дерево. С помощью дерева кратчайших путей для узла 1 можно получить таблицу маршрутов для узла 1, показывающую исходящий путь. По которому нужно направлять пакеты к узлу назначения. Подобная таблица маршрутов может быть составлена для каждого узла, являющегося источником сообщений. В случае централизованных вычислений каждая таблица маршрутов затем может быть направлена в соответствующий узел. В случае же децентрализованного, или распределенного выбора маршрутов, как в обсуждаемом ниже алгоритме сети ARPA, каждый узел выполняет свои вычисления, используя ту же самую глобальную информацию и генерируя собственное дерево и соответствующую таблицу маршрутов.

Алгоритм Флойда

Алгоритм имеет форму алгоритма Форда - Фалкерсона, т.е. одного из классов алгоритмов, впервые предложенного Флойдом.

Он также состоит из двух частей: начального шага и расчета кратчайших путей, которые повторяются до завершения алгоритма. Здесь кратчайшее расстояние представляет собой расстояние до данного узла от узла 1, например, рассматриваемого как узел назначения. Алгоритм заканчивается, когда для всех узлов фиксируется их расстояние до узла 1 (узла получателя) и отмечаются следующие узлы по направлению к узлу назначения по кратчайшему пути. Построение таблицы маршрутов с использованием алгоритма Флойда требует повторного или параллельного применения этого алгоритма для каждого узла назначения, что дает в результате набор меток для каждого узла, причем каждая метка дает информацию о маршруте (следующем узле) и расстоянии до конкретного узла назначения.

Дадим опять только неформальное описание алгоритма. Каждый узел v имеет метку (n, D(v)), где D(v) представляет текущую величину кратчайшего расстояния от узла до получателя, а n - номер следующего узла по текущему рассчитанному кратчайшему пути.

1. Начальный шаг. Если узел назначения - узел 1, то устанавливаем D(1)=0 и отмечаем все остальные узлы (· , ¥).

2. Отметка кратчайшего расстояния для всех узлов. Для каждого узла v¹1 выполняется следующее: обновляются величины D(v) путем использования текущего значения D(w) для каждого соседнего узла w и вычисления D(w)+l(w,v) с последующим выполнением операции

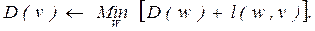
Метка v обновляется путем замены n номером смежного узла, что минимизирует только что приведенное выражение, и путем замены D(v) вновь полученным значением. Операция повторяется для каждого узла, пока не прекратятся дальнейшие изменения. (Тогда алгоритм завершается, и во всех узлах фиксируются метки как об их кратчайших расстояниях от узла 1, так и следующие соседние узлы по кратчайшему пути.)

Пример рассмотрим опять на рис.1. Обращаясь ко второй части алгоритма и применяя ее в циклическом порядке для узлов 2-6, находим, что алгоритм завершается после двух циклов. Эти циклы и полученные в результате метки каждого цикла, приводятся в табл.1.2 (любой другой порядок обхода узлов приводит к тому же самому окончательному результату).

Таблица 1.2 Алгоритм Флойда; рис.1

Цикл	Метки, узел®
Начальный		(· , ¥)	(· , ¥)	(· , ¥)	(· , ¥)	(· , ¥)
		(1,2)	(1,5)	(1,1)	(4,2)	(5,4)
		(1,2)	(5,3)	(1,1)	(4,2)	(5,4)

Таким образом, в цикле 1 нужно отметить, что узел 2 является «ближайшим» к его соседу 1. Его результирующая новая стоимость равна D(v)=D(1)+l(1,2)=2. Следовательно, метка, как это и указано, имеет вид (1,2). Переходя к узлу 3, приходим к необходимости выбора стоимостей между D(2)+l(2,3)=5 или D(1)+l(1,3)=5. Выбирая произвольно D(1)+l(1,3), получим (1,5), что показано в таблице (при другом выборе получится то же самое). Аналогично получаются другие результаты. В цикле 2 узел 3 имеет теперь пять соседних узлов с конечными значениями D(w), между которыми нужно произвести выбор. Минимальное значение D(w)+l(w,3) равно D(5)+l(5,3), и метка узла 3, как показано, меняется на (5,3). Другие узлы не меняют своих меток, и алгоритм завершается. Опять же дерево кратчайших путей с корнем в узле 1, как показано на рис.2а, может быть получено путем обхода меток каждого узла. В результате, узел 2 соединяется с узлом 1, узел 3 - с узлом 5, узел 4 - с узлом 1, узел 5 - с узлом 4 и узел 6 - с узлом 5. Иначе, таблица маршрутов или значение следующего узла в каждом узле по направлению к узлу 1 в точности является первым числом каждой двузначной метки, что и указывалось выше. Для получения полной таблицы маршрутов в каждом узле алгоритм В должен быть повторен для каждого узла, принимаемого в качестве узла назначения.

Алгоритм, подобный алгоритму Флойда, применяется для централизованных вычислений маршрутов в сети Tymnet.

3. Контрольные вопросы

1. Какая модель является международным стандартом для передачи данных?

1) ISO

2) OSI

3) ASCII

2. Сколько уровней выделяется в модели взаимодействия открытых систем?

1) Шесть

2) Семь

3) Восемь

3. В каком виде выполняется физический уровень?

1) В аппаратном

2) В программном

3) Как в аппаратном, так и в программном

4. Что подразумевается под набором правил и форматов, определяющих взаимодействие объектов одного уровня модели?

1) Сервис

2) Пакет с информацией

3) Протокол

5. Какой уровень модели OSI является наиболее близким к пользователю?

1) Прикладной

2) Представительный

3) Сетевой

6. Какому уровню принадлежит функция маршрутизации пакетов, передаваемых через сеть?

1) Канальному

2) Сетевому

3) Физическому

7. Установление путей между узлами источника и получателя осуществляется в центре управления сетью, а затем полученная в результате информация распределяется по всем узлам сети. Что это за тип выбора кратчайших путей?

1) Централизованный

2) Децентрализованный

3) Распределенный

8. Основой какого типа выбора кратчайших путей служит алгоритм Флойда?

1) Централизованного

2) Децентрализованного

3) Комбинированного

9.Какие применяться методы маршрутизации?

Централизованный и децентрализованный

Централизованный и декомпозиционный

Декомпозиционный и коммутативный

10.Какие недостатки имеют централизованные методы для поиска кратчайших путей?

Для реализации необходимо в 2*Е раз больше итераций.

Для реализации необходимо знание глобальной структуры сети

Реализуется не для всех вычислительных сетей

11.Какие недостатки имеют децентрализованные методы для поиска кратчайших путей?

Поиск выполняется дольше, чем при использовании централизованных методов.

Могут приводить к конфликтам в системе

Узлам приходится обмениваться между собой стоимостью маршрутов в ходе поиска.

12.К какому типу относится метод Дейкстры?

Коммутативный

Централизованный

Децентрализованный

4. Варианты заданий для самостоятельной работы

1. Дана сеть

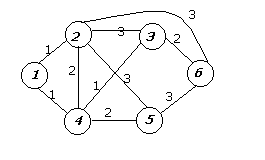Получить дерево кратчайших путей и таблицу маршрутов методом Флойда.

2. Дана сеть

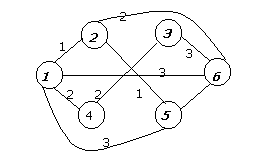Получить дерево кратчайших путей и таблицу маршрутов методом Дейкстры.

3. Дана сеть.

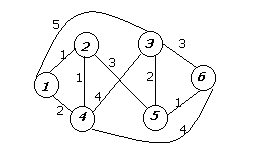Получить дерево кратчайших путей и таблицу маршрутов методом Флойда.

4. Дана сеть.

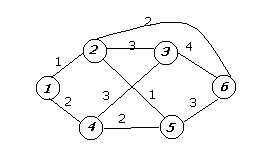
Получить дерево кратчайших путей и таблицу маршрутов методом Дейкстры.

5. Дана сеть.

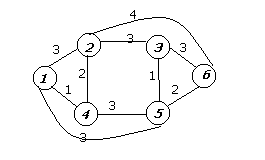Получить дерево кратчайших путей и таблицу маршрутов методом Флойда.

6. Дана сеть.

Получить дерево кратчайших путей и таблицу маршрутов методом Дейкстры.

7. Дана сеть.

Получить дерево кратчайших путей и таблицу маршрутов методом Флойда.

8. Дана сеть.

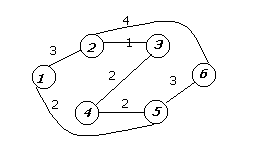Получить дерево кратчайших путей и таблицу маршрутов методом Дейкстры.

9. Дана сеть.

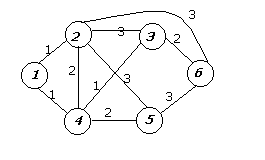
Получить дерево кратчайших путей и таблицу маршрутов методом Флойда.

10. Дана сеть.

Получить дерево кратчайших путей и таблицу маршрутов методом Дейкстры.

11. Дана сеть.

Получить дерево кратчайших путей и таблицу маршрутов методом Дейкстры.

12. Дана сеть.

Получить дерево кратчайших путей и таблицу маршрутов методом Дейкстры.

Содержание отчета

5.1. Титульный лист.

5.2. Краткое теоретическое описание

5.3. Задание на лабораторную работу, включающее математическую

формулировку задачи.

5.4. Результаты выполнения работы, включающие схему алгоритма,

тексты программ, результаты вычислений.

Литература

1. Microsoft Corporation. Компьютерные сети. Учебный курс/Пер. с англ. - М.: Издательский отдел ”Русская редакция” ТОО ”Channel Trading Ltd.”.1997.

2. Блэк Ю. Сети ЭВМ. Протоколы, стандарты, интерфейсы. - М.: Мир,1990.

3. Вентцель Е.С. Исследование операций: задачи, принципы, методология .– М.: Наука, Главная редакция физико - математической литературы, 1980.

4. Каган Б.М. Электронные вычислительные машины и системы. - М.: Энергоатомиздат, 1991.

5. Ключко В.И. Кодирование информации . Курс лекций.. -Краснодар, КГТУ, 1998.

6. Методы управления ресурсами вычислительных систем:Учебное пособие/П.П. Кравченко, А.Г. Чефранов; Таганрог. радиотехн. ин-т. Таганрог, 1991.

7. Нанс Б. Компьютерные сети. - М.: БИНОМ, 1996.

8. Озкарахан Э. Машины баз данных и управление базами данных: Пер. с англ.– М.: Мир, 1989.

9. Основы теории вычислительных систем/С.А.Майоров, Г.И. Новиков,Т.И. Алиев и др. - М.: Высшая школа, 1987.

10. Семенов М.И., Лойко В.И., Барановская Т.П.Автоматизированные информационные технологии в экономике: Учебное пособие для агроэкономических специальностей вузов/Под общей ред. И.Т.Трубилина. - Краснодар: издательство КубГАУ, 1998.

11. Смирнов А.Д. Архитектура вычислительных систем. - М.: Наука, 1990.

12. Советов Б.Я.Информационная технология: Учеб. для вузов по спец. ”Автоматизир. системы обработки информ. и упр.”. - М.: Высш. шк.,1994.

13. Советов Б.Я., Яковлев С.А. Построение сетей интегрального обслуживания. - Л.: Машиностроение. Ленингр. отд - ние,1990.

14. Шварц М. Сети связи: протоколы, моделирование и анализ:В 2-х ч.:Пер. с англ. - М.: Наука, 1992.

15. Якубайтис Э.А. Информационные сети и системы. - М.: Финансы и статистика,1996.

Содержание

Организационно-методические указания_________________________________ 3

Лабораторная работа №1_______________________________________________ 4

Лабораторная работа №2______________________________________________ 14

Лабораторная работа № 3_____________________________________________ 21

Лабораторная работа N4______________________________________________ 30

Лабораторная работа №5______________________________________________ 37

Лабораторная работа №6______________________________________________ 46

Лабораторная работа № 7_____________________________________________ 61

Литература__________________________________________________________ 73