Дифференциальные уравнения невозмущенного движения искусственных спутников Земли
Уравнения движения спутников Земли выводят на основе фундаментальных законов механики Ньютона и закона всемирного тяготения. Законы Кеплера получаются при этом как следствия.
Согласно закону всемирного тяготения Земля (массой МÅ) и спутник (массой m) притягивают друг друга с силой:
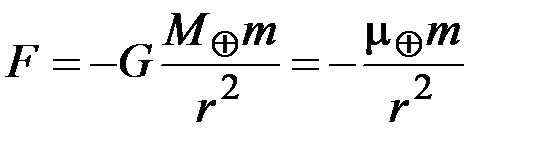 . (1.22)
. (1.22)
С другой стороны, по второму закону Ньютона
F = ma, (1.23)
где a – ускорение.
Приравнивая правые части уравнений и проецируя ускорение на оси инерциальной системы координат, получаем:
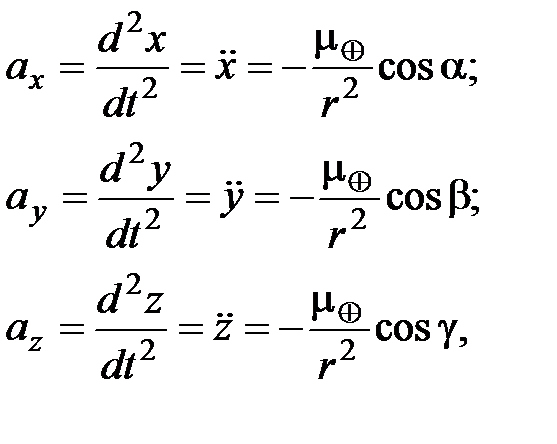 (1.24)
(1.24)
| где | 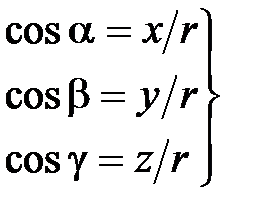 | — направляющие косинусы геоцентрического радиус-вектора 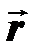 спутника. спутника. |
Подставляя в (1.26) выражения для направляющих косинусов, имеем:
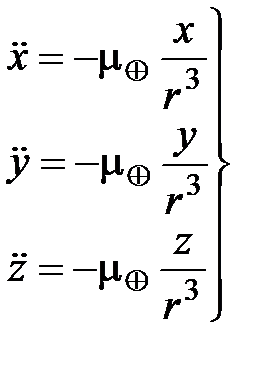 ; (1.25)
; (1.25)
Уравнение (1.25) представляет собой систему трех нелинейных дифференциальных уравнений второго порядка, в результате интегрирования которой для любого момента ti можно получить координаты x, y, z и составляющие скорости 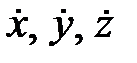 ИСЗ. При этом должны быть известны начальные условия (всего 6) интегрирования, например, координаты x0, y0, z0 и составляющие скорости
ИСЗ. При этом должны быть известны начальные условия (всего 6) интегрирования, например, координаты x0, y0, z0 и составляющие скорости 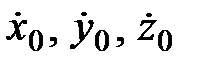 для начальной эпохи t0.
для начальной эпохи t0.
Начальные условия можно задать элементами кеплеровой орбиты, которыми, как правило, являются: большая полуось a; эксцентриситет Î; долгота восходящего узла W; аргумент перицентра w; наклонение орбиты J; время прохождения спутника через перицентр tп.
Возмущенное движение ИСЗ
Рассмотрение движения в гравитационном поле сферической Земли с равномерным распределением масс и без учета других факторов является идеализацией и служит первым приближением в решении задачи о движении ИСЗ.
Реальное движение отличается от идеализированного наличием большого числа других сил (помимо гравитационной), каждая из которых существенно меньше силы тяготения Земли. Однако, именно вследствие действия этих возмущающих сил, элементы кеплеровой орбиты ИСЗ непрерывно изменяются.
Основными возмущающими факторами являются:
· неравномерность гравитационного поля Земли и его аномалии;
· сопротивление атмосферы;
· притяжение Луны, Солнца и других планет;
· магнитное и тепловое поле Земли;
· солнечное излучение;
· действие заряженных и нейтральных частиц;
Дифференциальные уравнения возмущенного движения КЛА можно записать в виде:
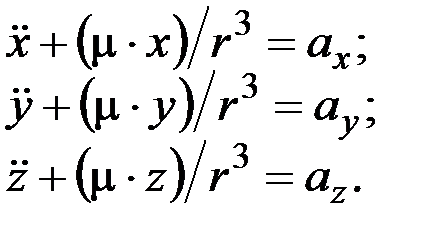 (1.26)
(1.26)
где ax, ay, az – суммарные значения ускорений по осям инерциальной системы координат, обусловленные действием возмущающих сил.
Решения этих дифференциальных уравнений: т.е. x, y, z, 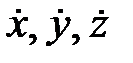 уже не постоянны, а являются некоторыми функциями элементов орбиты и времени. Их совокупность определяет мгновенную орбиту.
уже не постоянны, а являются некоторыми функциями элементов орбиты и времени. Их совокупность определяет мгновенную орбиту.
