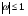Замена переменных в двойном интеграле

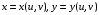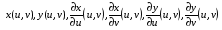При вычислении интегралов часто бывает удобно сделать замену переменных , где – непрерывны в некоторой области . Впоследствии мы будем часто писать просто 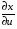вместо 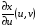и т.п. и, кроме того, говорить при выполнении вышеупомянутых условий, что x и y – непрерывно дифференцируемые в Δ функции. Будем также использовать обозначения

.

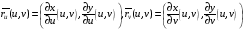Пусть при этом формулы 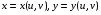задают взаимно-однозначное отображение квадрируемых областей: 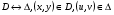. Кроме того, потребуем, чтобы всюду на области Δ не равнялся 0 якобиан отображения
.

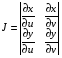Теорема 1.5.При сформулированных выше условиях для непрерывной на функции 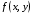выполняется равенство

.

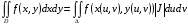►Строгое доказательство этой теоремы потребовало бы значительных усилий из-за обилия технических деталей. Мы изложим здесь схему доказательства. Во-первых, оба интеграла в формулировке теоремы существуют, поскольку 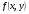– непрерывная функция.

Рассмотрим разбиение области Δ прямыми, параллельными осям u и v. Рассмотрим его часть, имеющую вид прямоугольника с вершинами

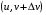
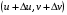
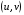
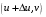
При отображении 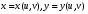эти точки перейдут, соответственно, в точки

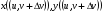
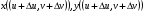
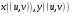
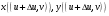
Далее, при

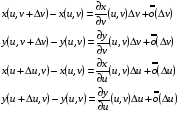
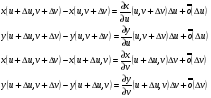
При малых 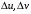производные 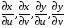, вычисленные в точках 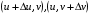, мало отличаются от соответствующих производных, вычисленных в точке 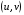, поэтому и определённые выше векторы 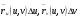мало отличаются от векторов 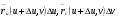и 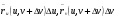, соответственно, и рассматриваемый четырёхугольник представляет собой «почти параллелограмм».

Как известно из курса линейной алгебры, площадь параллелограмма со сторонами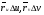

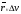
равна модулю определителя, составленного из координат этих векторов,

,

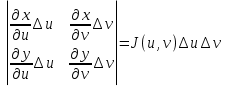т.е равна 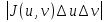. Поэтому при сделанном преобразовании координат интегральная сумма

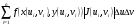
близка по величине к интегральной сумме

.

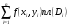Точнее говоря, можно доказать, что соответствующие интегральные суммы для интегралов, стоящих в правой и левой частях доказываемого равенства, отличаются друг от друга на стремящуюся к нулю величину. Поэтому и интегралы совпадают.◄

Замечание. Утверждение теоремы сохранится, если условие взаимной однозначности отображения нарушится на множестве нулевой площади.

Переход к полярным координатам. Вычисление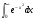

Пусть требуется вычислить 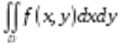по области , которая задаётся в полярных координатах условиями

Сделаем замену переменных

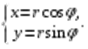
При этой замене нарушается взаимная однозначность отображения. Точке (0,0) соответствует целый отрезок 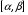на оси 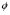. Однако и точка, и отрезок имеет нулевую площадь, и теорема, с учётом замечания, справедлива. Осталось вычислить якобиан преобразования.

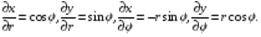
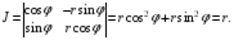
Следовательно,

.

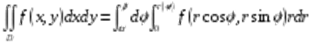Полярные координаты бывают очень полезны при вычислениях. Рассмотрим пример.

Пример. Найти .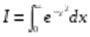

Решение. 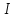— это несобственный интеграл, и прежде всего следует установить его сходимость. По определению,

.

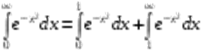Первый из интегралов — собственный, второй — сходится по 1-й теореме о сравнении, так как при 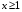справедливо неравенство_,из которого следует, что 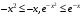, а интеграл 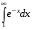, очевидно, сходится.

Обозначим 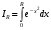(очевидно, 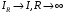). Тогда, поскольку обозначение переменной интегрирования можно выбрать произвольным, т.е.

,

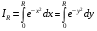имеем

,

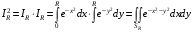где 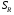— квадрат, а 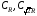— четверти круга, соответственно, радиусов и 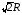. Так как 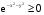, то по свойствам 2 , 3 двойного интеграла .

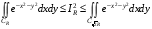В интеграле 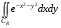перейдем к полярным координатам:

.

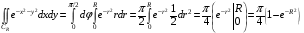Аналогично,

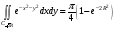
и .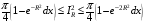

При стремлении 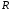к 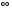получаем, что

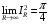, то есть .

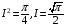Тройные интегралы

Рассмотрим кубируемое множество 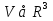. Считаем, что оно ограничено конечным числом кусочно-гладких поверхностей . Разбиение на части 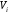также осуществляется кусочно- гладкими поверхностями. Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции 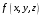, разбиения множества 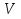на части и для выбранных точек 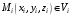интегральную сумму

,

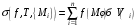где 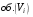обозначает объем части .

Определение. Пусть такое число, что .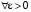

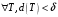
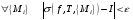Тогда мы говорим, что функция интегрируема на множестве , число есть интеграл функции по множеству и обозначаем это так: .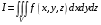

Как и в случае двойного интеграла, выполняются свойства 1-6. Полезное упражнение - переформулировать их для тройного интеграла .

Теорема 2.1. Ограниченная на кубируемом множестве функция 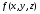интегрируема тогда и только тогда, когда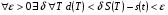

(На экзамене ограничиваемся формулировкой).

Из этого критерия следует теорема.

Теорема 2.2. Если функция непрерывна на кубируемом множестве , то интегрируема на этом множестве.

(На экзамене достаточно формулировки).

Точно также можно убедиться в том, что если точки разрыва лежат на конечном числе кусочно-гладких поверхностей, лежащих на и разбивающих на кубируемые области, то интегрируема на .

Вычисление тройного интеграла производится по следующему правилу.

Теорема 2.3.Пусть задана следующими неравенствами:

,

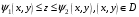где — квадрируемая область на плоскости, 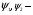непрерывные функции. Тогда

.

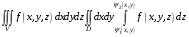Замечание. Если область задана неравенствами 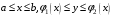, где — непрерывные функции, то

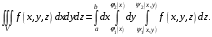
Сформулируем общую теорему о замене переменных.

Теорема 2.4. Пусть отображение 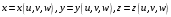устанавливает взаимно однозначное соответствие между областям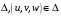и и 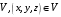, причем функции 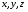— непрерывно дифференцируемые и ни в одной точке 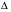.Пусть всюду в области

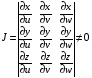
Пусть — непрерывная функция. Тогда

.

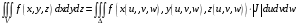Как и для двойного интеграла, теорема остается верной в случае нарушения ее условий на множестве нулевого объема.

Пример 1. Переход к цилиндрическим координатам. Он осуществляется с помощью функций: .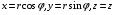

При этом якобиан равен

.

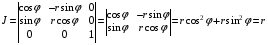Пример 2. Переход к сферическим координатам осуществляется функциями .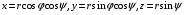

Якобиан преобразования равен

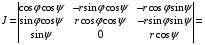
(разложение определителя по 3-й строке)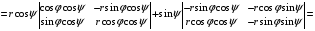

(выделение общих множителей у столбцов)

.

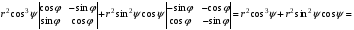
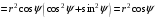Часто используется интеграл (вы встретите его при вычислении двойных, тройных интегралов при переходе к сферическим или цилиндрическим координатам)

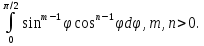
Сведем его к значениям эйлеровых интегралов см. приложение 3:

|=

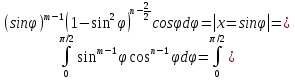
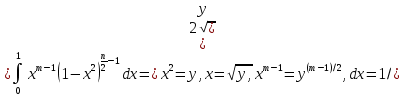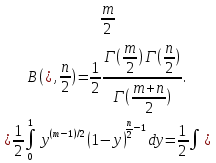
Эйлеровы интегралы

Гамма-функция

Рассмотрим несобственный интеграл

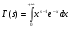(1)

как функцию от s и выясним область ее определения. Для этого представим интеграл (1) в виде суммы несобственных интегралов

.

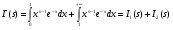Поскольку 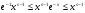для всех 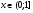и всех 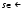, а эталонный интеграл 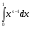сходится при 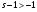; т.е. при 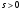, и расходится при 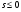, то, по признакам сравнения несобственных интегралов, интеграл 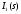сходится при всех и расходится при .

Поскольку 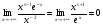для любого и 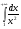сходится, то по аналогичному признаку сравнения заключаем, что несобственный интеграл 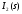сходится при всех .

Окончательно, несобственный интеграл (1) сходится только при ; т.е. областью определения гамма-функции Г(s) служит множество всех положительных чисел.

Интегрируя по частям (подстановка верхнего предела означает переход ),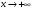

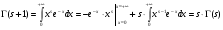. (2)

Формула 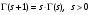, задает функциональное уравнение для гамма-функции.

Покажем, что при 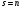, где n-натуральное число, 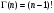; т.е. гамма-функция есть обобщение понятия факториала. При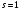

.

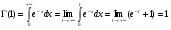При , где n-натуральное число большее 1, пользуемся функциональным уравнением

.

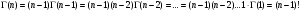Положив 0!=1, получим, что равенство выполняется для всех натуральных чисел.

Известно, что гамма-функция Эйлера бесконечно дифференцируема на , выпукла вниз и её минимум приходится в точке интервала 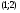, поскольку .

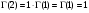Бета-функция

Эйлером предложен также несобственный интеграл

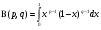(3)

как функция параметров 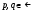, которую называют бета-функцией. Представим интеграл (3) в виде суммы двух слагаемых

,

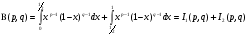где 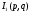имеет особенность только в точке 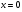, а 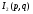- только в точке .

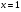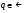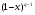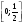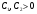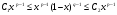Поскольку для любого функция положительна, непрерывна и ограничена на отрезке , то существуют постоянные , что для всех 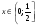и всех 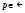. Поэтому, как и в предыдущем пункте, убеждаемся, что интеграл сходится для всех только при .

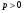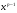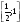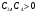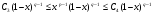Аналогично, функция положительна, непрерывна и ограничена на отрезке для любого , и, следовательно, существуют , что для всех 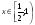и всех .

Поэтому несобственный интеграл сходится для каждого только при .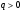

Окончательно, бета-функция 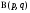определена только для и .

Совершая в интеграле (3) замену переменной интегрирования 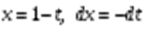, получим

. (4)

Формула (4) указывает на свойство симметричности бета-функции Эйлера.

Интегрируя в (3) по частям и используя разложение 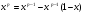, получим

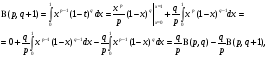
откуда

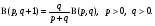(5)

В силу симметричности функции имеем также

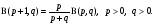(5’)

Формулы (5) и (5’) называют функциональными уравнениями для бета-функции.

Если 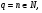то согласно (5)

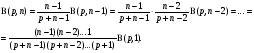
Но

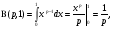
Так что

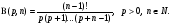(6)

Если 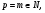то (6) принимает вид

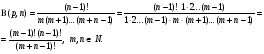
Так как 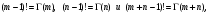то мы доказали частный случай

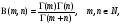
замечательной формулы Эйлера

Гамма-функция и бета-функция, как и экспоненциальная функция, играют фундаментальную роль в математике и её приложениях.

Сформулируем без доказательств несколько важных свойств этих функций.

Для любого 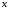, 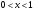выполняется равенство 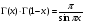, называемое формулой дополнения. Из этого, в частности, следует, что

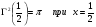и, следовательно, .

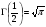Бета-функция допускает ещё представление в виде интеграла

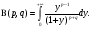
Часто используется интеграл (Вы встретите его при вычислении двойных, тройных интегралов при переходе к полярным, сферическим или цилиндрическим координатам)

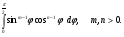
Сведём его к значениям эйлеровых интегралов:

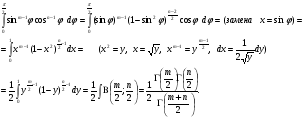
Формула Стирлинга

К настоящему моменту времени свойства гамма-функции изучены достаточно глубоко. В частности, для неё доказано следующее асимпототическое представление

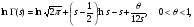(7)

называемоеформулой Стирлинга. Для натуральных 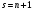, когда 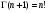, формула (7) после несложных преобразований принимает вид

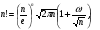где