Ряд Фурье для произвольного интервала.

Разложение периодической функции с периодом L.

Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.

Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид

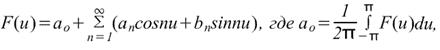
Где коэффициенты ряда Фурье,

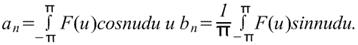
Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования - от -L/2 до L/2 вместо - π до π. Следовательно, ряд Фурье для зависимости от х имеет вид

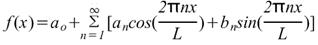
Где в диапазоне от -L/2 до L/2 коэффициенты ряда Фурье,

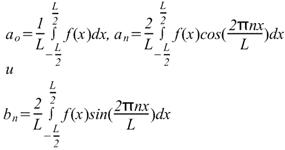
(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)

Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.

Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде.

Разложение по косинусам в диапазоне от 0 до L имеет вид

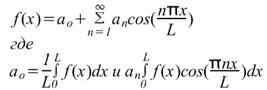
5.Дифференциальные уравнения первого порядка,основные понятия.

Дифференциальным называют уравнение, из которого требуется определить искомую функцию и которое содержит не только эту функцию, но и ее производные или дифференциалы.

Если неизвестная функция является функцией одной переменной, то такое уравнение называют обыкновенным дифференциальным уравнением.

Пример 1.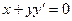

Если неизвестная функция является функцией нескольких переменных, то такое уравнение называют уравнением в частных производных.

Пример.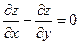

Порядком дифференциального уравнения называют наивысший порядок содержащихся в нем производных.

Пример 2. 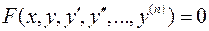дифференциальное уравнение 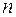-го порядка.

Решением дифференциального уравнения называют функцию 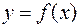, дифференцируемую по крайней мере 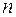раз, обращающую его при подстановке в уравнение в тождество.

Отыскание всех решений и описание их свойств является основными задачами теории дифференциальных уравнений. Процесс отыскания решений называют интегрированием этого уравнения.

Пример 3.

Найти все решения дифференциального уравнения .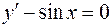

Интегрируя, получим .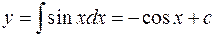

Общим решением дифференциального уравнения называют решение, которое существенно зависит от произвольной постоянной с. Общее решение, полученное в неявном виде называется общим интегралом дифференциального уравнения.

y = - cos x +c – общее решение.

y + cos x = с – общий интеграл.

Решение дифференциального уравнения, которое получается из общего решения при фиксированном значении постоянной c , называют частным решением.

Пусть М(0,2), с= 2+ сos(0); с = 3. y = -cos x + 3 – частное решение, то есть мы выделяем кривую, которая проходит через точку (0,2).

Кривые y = - cos x +c называются интегральными кривыми дифференциального уравнения .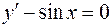

Уравнение вида F(x,y, 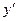)=0 (1) называется дифференциальным уравнением первого порядка.

Задача Коши для дифференциального уравнения первого порядказаключается в отыскании решения уравнения (1), удовлетворяющего начальному условию 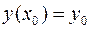. Геометрически это означает определение интегральной кривой, проходящей через точку .

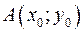Теорема Пикара. Если в уравнении 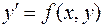функция 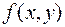определена и непрерывна в окрестности точки 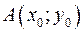и, кроме того, имеет частную производную 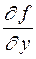, то задача Коши имеет единственное решение, являющееся дифференцируемой функцией. Если в точке 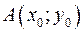условия теоремы Пикара нарушаются, то задача Коши может иметь несколько решений или не иметь их вовсе. В первом случае через точку 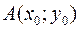проходит несколько интегральных кривых. Точки, в которых происходит нарушение условий теоремы Пикара, называют особыми. Дополнительные решения задачи Коши, возникающие при этом, также называют особыми.

Кратные интегралы.

Двойные интегралы

Определение двойного интеграла и критерий интегрируемости

Определение двойного интеграла:

Мы будем рассматривать функции 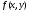, определённые на квадрируемом (то есть имеющем площадь) множестве 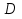. Практически всегда представляет собой фигуру, ограниченную кусочно-гладкой кривой, или конечное объединение таких фигур. Далее, говоря о квадрируемом множестве, мы ограничиваемся рассмотрением именно таких множеств.

Если вспомнить теорию определённого интеграла, то мы начали её изложение с понятия разбиения 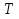отрезка 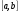. По аналогии, определим разбиение квадрируемого множества , как представление множества в виде объединения конечного числа квадрируемых частей, .

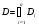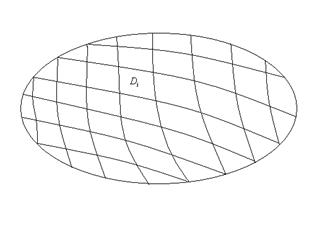
Можно считать, что разбиение на части 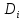также осуществляется с помощью спрямляемых(т.е. имеющих длину) кривых, то есть все также являются фигурами с кусочно-гладкими границами, либо конечными объединениями таких фигур.

В одномерном случае мы рассматривали длины частей разбиения 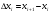. В двумерном случае обобщением понятия длины 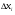будет площадь . Однако нам потребуется также понятие диаметра множества 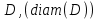. Эта величина определяется, как точная верхняя грань расстояний между точками множества . В частности, если – круг, то 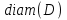– это как раз длина диаметра круга в обычном смысле. В общем понятие диаметра множества поясняет рисунок:

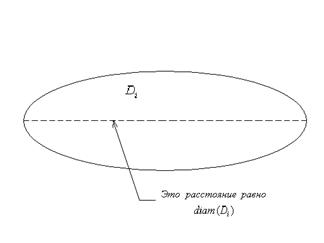
Ясно, что если 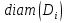невелик, то и площадь также невелика, поскольку неравенство 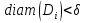означает, что содержится некотором в круге радиуса 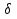и имеет площадь не больше, чем .

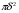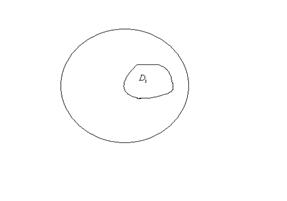
Действительно, возьмём произвольную точку множества в качестве центра этого круга. Так как , остальные точки лежат внутри круга.

Однако площадь множества может быть невелика, а достаточно велик. Пример – очень тонкий прямоугольник.

Определим диаметр 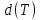разбиения T как наибольший из диаметров частей этого разбиения. Далее, как и в одномерном случае, выберем точки 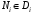(было: 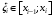).Пусть 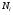имеет координаты 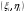. Важную роль в дальнейшем будет играть понятие интегральной суммы, определяемой равенством 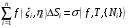. Так же, как и в одномерном случае, эта величина имеет простой геометрический смысл. Вспомним, что сумма 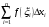представляла собой площадь ступенчатой фигуры вида:

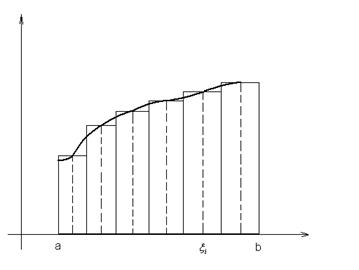
(для простоты считаем, что ).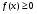

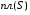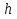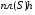Напомним, что объём цилиндра с основанием, имеющим площадь и с высотой равен . Поэтому интегральная сумма 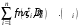равна объёму тела, состоящего из цилиндров с высотой 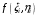(для простоты считаем, что 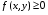) и основаниями .

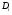Перейдём к основному определению.

Определение.Пусть 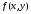- ограниченная на квадрируемом множестве функция. Пусть 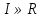. Если

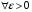
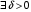
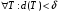
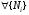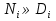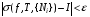_, , , (1)

то будем говорить, что f – интегрируемая на функция и что число 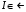является её интеграломна этом множестве. Используется обозначение .

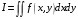Иногда используют обозначение .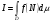

Замечание.Это определение несколько отличается от определения обычного определённого интеграла, в котором отсутствовало требование ограниченности функции 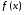. Дело в том, что для обычного определённого интеграла из выполнения условия (1) следовало необходимое условие интегрируемости: если 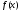интегрируема на , то ограничена на .

Для двойного интеграла из выполнения условия (1) не следует, что функция ограничена. Это условие, например, заведомо выполняется для любой определённой на множестве функции, если множество имеет равную нулю площадь. Для того, чтобы у двойного интеграла сохранились все важные свойства определённого интеграла и добавлено требование ограниченности функции.

Критерий интегрируемости

Критерий существования определённого интеграла 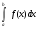формулировался в терминах сумм Дарбу, т.е. сумм вида 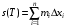, , 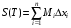где 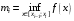, , 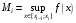то есть 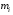- нижняя грань, а 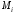- верхняя грань значений при .

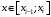Рассуждая аналогично, рассмотрим для ограниченной на квадрируемом множестве функции 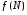числа 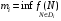, 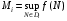(эти числа существуют ввиду предполагаемой ограниченности функции на и, значит, на всех. Определим суммы Дарбу равенствами 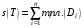, 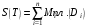. Эти величины представляют собой объемы тел, состоящих из цилиндров с основаниями и высотами, соответственно, 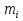и 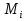. Ясно, что для любого разбиения при любом выборе точек 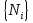выполнены неравенства между суммами Дарбу и интегральной суммой, соответствующей этому выбору точек: .

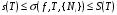На рисунке изображены тела, объёмы которых равны суммам Дарбу.

Нижняя сумма Дарбу

Верхняя сумма Дарбу

Вполне аналогично одномерному случаю можно доказать критерий существования двойного интеграла.

Теорема 1.1.Ограниченная на квадрируемом множестве функция интегрируема тогда и только тогда, когда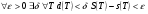

(На экзамене ограничиваемся формулировкой).

Из этого критерия следует теорема.

Теорема1.2.Если функция непрерывна на квадрируемом множестве , то интегрируема на этом множестве.

(На экзамене достаточно формулировки).

Свойства двойных интегралов

Свойство 1. Если 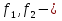- интегрируемые на квадрируемом множестве функции, а 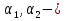числа, то

.

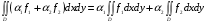Иными словами, интеграл - линейный функционал.

Свойство 2. Если 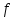- интегрируема на объединении квадрируемых множеств 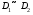, то

,

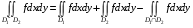причем если площадь пересечения 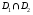равна 0, то 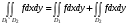. (Аддитивность интеграла по множеству).

Свойство 3.Если- интегрируемая на квадрируемом множествефункция и 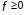, то .

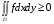Свойство 4.Если - интегрируемые на квадрируемом множестве функции и 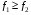, то .

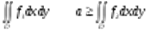Свойство5.Если- интегрируемая на квадрируемом множествефункция , причем .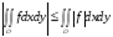

Свойство 6.Если- интегрируемая на квадрируемом множествефункция , то функция 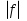– также интегрируемая, причем 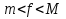где т, М ограничивающие множество значений функции числа, товыполняются неравенства ,

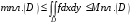т.е.существует число 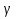, удовлетворяющее неравенствам 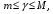для которого

.

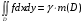Если, кроме того, множество – связное* и- непрерывна на нём,то существует точка 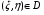, для которой

.

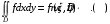Доказывать эти свойства мы не будем, поскольку их доказательства вполне аналогичны доказательствам свойств обычного интеграла.

В конце п.1.2. отмечено, что если -непрерывная на множестве функция, то - интегрируема на . Свойство 2 позволяет утверждать, что если имеет разрывы налишь вдоль конечного числа спрямляемых линий, разбивающихна квадрируемые области, то - интегрируема на , т.к., по свойству 2, интеграл по есть просто сумма конечного числа интегралов по полученным частям (на которых непрерывна и, значит, интегрируема).

*Примечание.Связным множеством на плоскости назовем такое множество, любые две точки которого можно соединить кусочно-гладкой кривой, лежащей в этом множестве.

3. Вычисление двойного интеграла сведением к повторному интегралу

Двойной интеграл – новый объект и мы укажем способ его вычисления сведением к повторному вычислению определённого интеграла. Сначала рассмотрим двойной интеграл по прямоугольной области 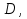стороны которой параллельны осям координат.

Теорема 1.3.Пусть для функции 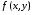существует двойной интеграл 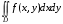по области 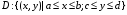. Кроме того, пусть для любого 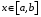существует .

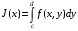Тогда существует и интеграл, называемый повторным:

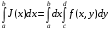
и выполняется равенство

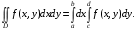(2)

►Разобьём прямоугольник на прямоугольники, обозначенные 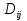, прямыми, проходящими параллельно оси 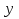через точки 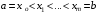и прямыми, параллельными оси 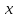и проходящими через точки 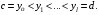Таким образом,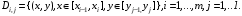

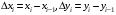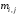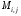Пусть , числа и , соответственно, равны нижней и верхней граням функции 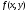на 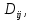откуда 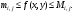Проинтегрируем эти неравенства по на отрезках :

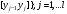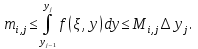
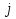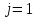Суммируя эти неравенства по от до 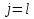, получаем

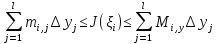
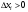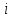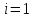Умножим все части этих неравенств на и суммируем полученные неравенства по от до :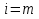

.

Поскольку 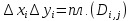, эти неравенства можно переписать в виде

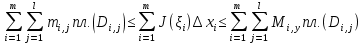
или

,

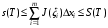где – разбиение на прямоугольник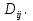и При 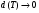стремится к нулю и величина 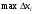. Кроме того, при также 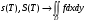. Значит, интеграл 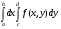существует и равен , что и утверждалось.◄

Замечания.

1. В случае, когда непрерывна навсе условия теоремы выполняются и равенство (2) справедливо.
2. Отметим, что интеграл 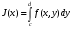представляет собой собственный интеграл, зависящий от параметра.

Рассмотрим случай криволинейной трапеции. Справедлива такая теорема:

Теорема 1.4 (Фубини).Пусть область задана неравенствами 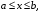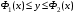, где 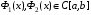. Пусть существует 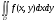и для любого существует 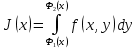. Тогда существует интеграл 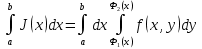и он равен .

►Так как 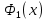непрерывна на 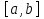, существует её минимальное значение 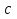на этом отрезке. Аналогично, существует максимальное значение 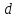функции 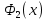на отрезке 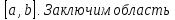в прямоугольник 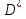, состоящий из точек 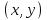, , 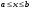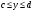. На этом прямоугольнике рассмотрим функцию

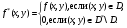
Условия предыдущей теоремы для функции 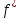выполнены. Она интегрируема в , равна 0 (и, значит, интегрируема) в 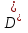. Следовательно, она интегрируема на всём множестве . При этом

.

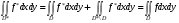Наконец, для любого 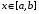выполнено равенство

.

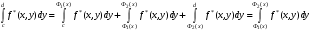По доказанному в предыдущей теореме,

,

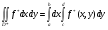откуда сразу получаем:

,

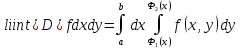что и требовалось доказать.◄

Следствие: Пусть 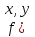) непрерывна в области , ограниченной сверху графиком функции 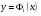, снизу - , где , a по бокам - отрезками вертикальных прямых х = а и х = b. Тогда

.

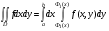►Из непрерывности 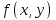сразу следует её интегрируемость на . Кроме того, для любого 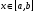функция непрерывна (а, значит, интегрируема по у). Все условия теоремы выполнены. ◄

Замечание. Если область можно ограничить так:
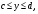
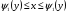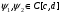, , то

.

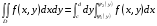Смысл этих теорем ясен – указан способ сведения двойного интеграла к собственным интегралам, зависящим от параметра.