Замена переменных в тройном интеграле.

При вычислении тройного интеграла, так как и двойного, часто применяется метод подстановки, т.е совершается преобразование переменных.

Пусть совершена подстановка 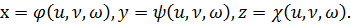Если эти функции имеют в некоторой области 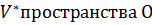( 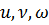) непрерывные частные произвондные и отличный от нуля определитель .

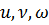I(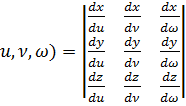

То справедлива формула замены переменных в тройном интеграле:

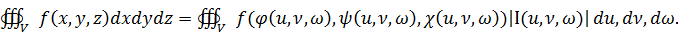(4)

Здесь I( 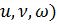-определитель Якоби, или якобиан преобразования .

Для вычисления тройного интеграла часто используют цилиндрические координаты. Положение точки M(x,y,z) в пространстве Оxyz можно определить заданием трёх чисел r, 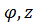. Где r-длина радиус-вектора проекции точки М на плоскость Оxy, 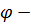угол, образованный этим радиус-вектором с осью Ох, z – аппликата точки М. Эти три числа (r, 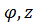.) называются цилиндрическими координатами точки М. Цилиндрические координаты точки связаны с декартовыми координатами следующим соотношением: x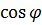=r , y=r 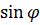, z=z.

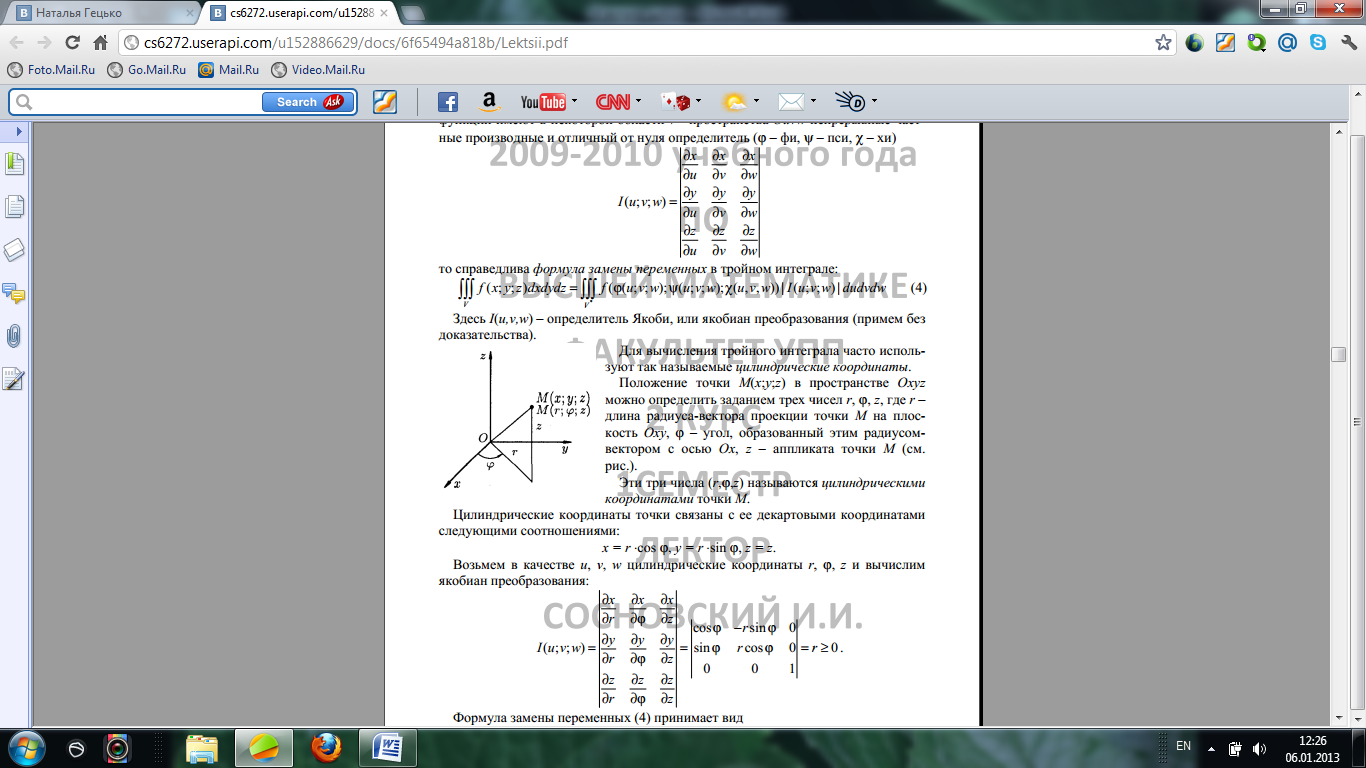
Возьмём в качестве 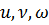цилиндрические координаты r, 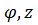и вычислим якобиан преобразования.
I( 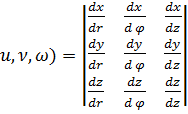= =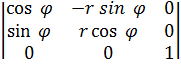r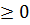

Формула для замены (4) принимает вид:

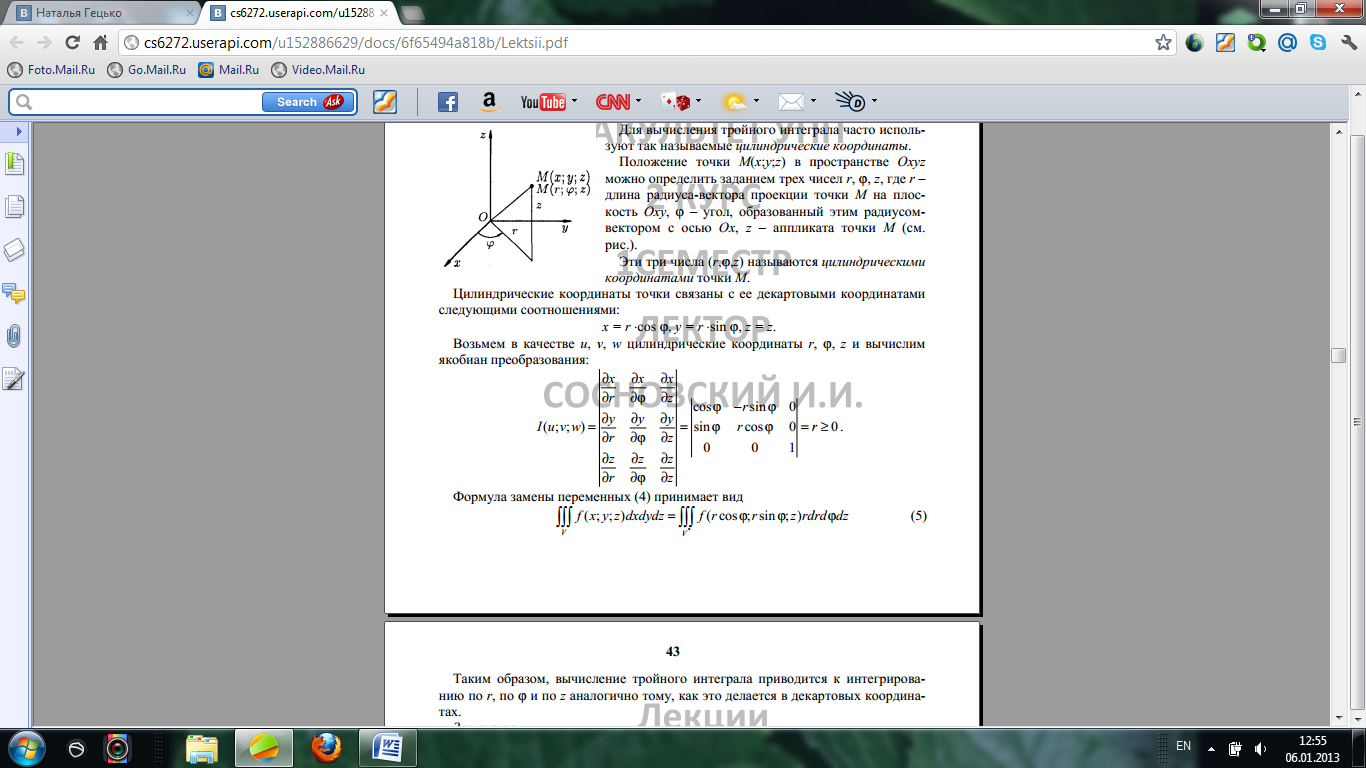
Таким образом, вычисление тройного интеграла приводится к интегрированию по r, 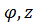, аналогично тому как это делается в декартовых координатах. Замечание: к цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.

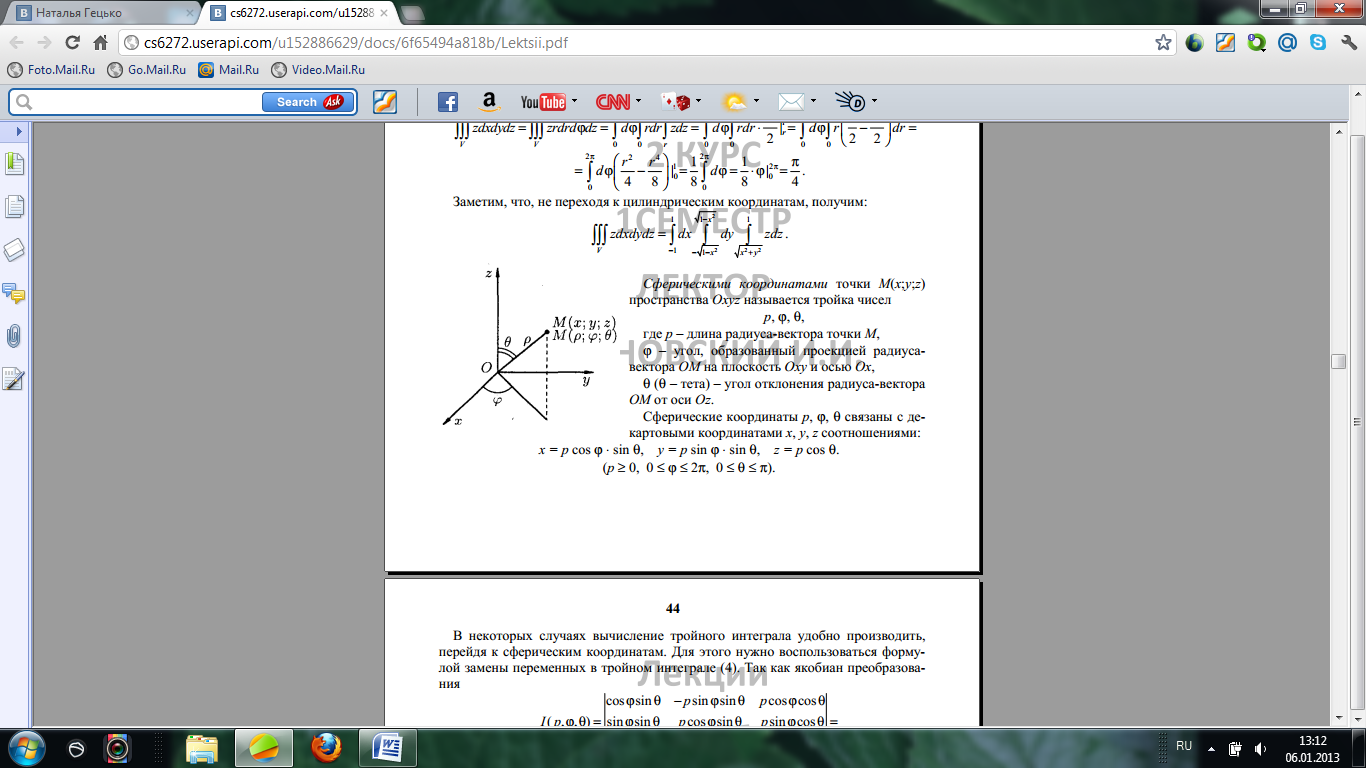
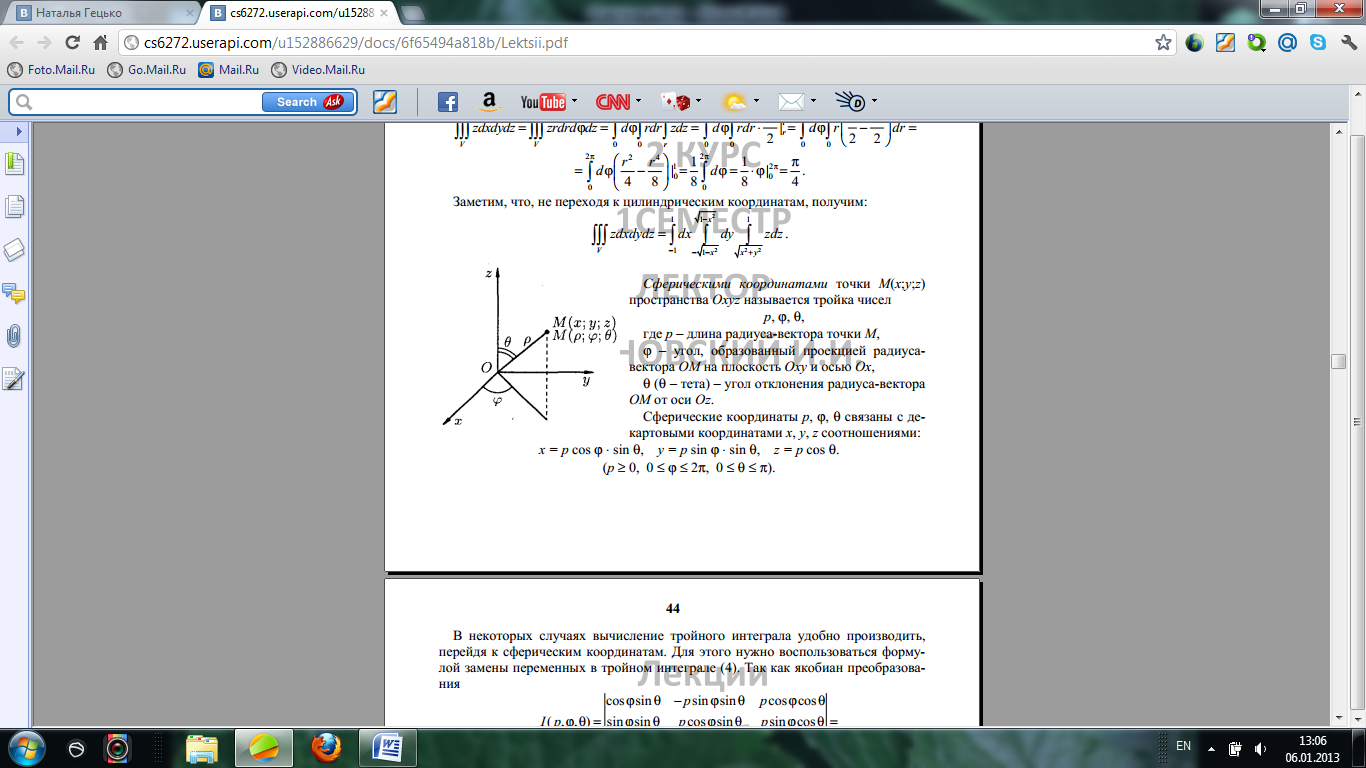Сферическими координатами точки М(x,y,z) пространства Оxyz называется тройка чисел p, 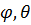. Где р – длина радиус вектора точки М, 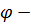угол, образованный проекцией радиус-вектора ОМ на плоскость Оху и осью Ох

В некоторых случаях вычисление тройного интеграла удобно производить, переходя к сферическим координатам .Для этого нужно пользоваться формулой замены переменных для тройного интеграла (4).Так как якобиан преобразования

I(p, 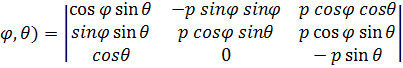=p sin 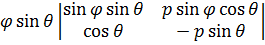+ p cos 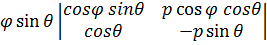= - 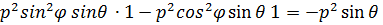, то

.

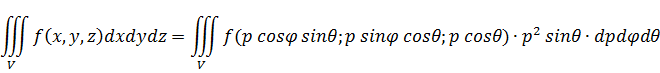
Замечание: переходить к сферическим координатам, удобно когда область интегрирования V есть шар или его часть, а так же если подинтегральная функция имеет вид f(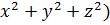

Криволинейные интегралы первого рода

Определение 1. Пусть L-плоская или пространственная линия на плоскости f(x,y) или пространстве f(x,y,z) непрерывная на L функция. Разобьем L произвольным образом на n элементарных частей. На каждой из элементарных частей выберем по точке Р_i и составим интегральную сумму 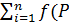_i) l_i, где l_i - длина частичной дуги.

Пусть λ=max {∆l_i}

Если существует конечный предел 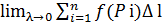_i, который не зависит от выбора точек dx называется криволинейным интегралом первого рода от функции f (P_i) по длине дуги L и обозначается 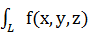в пространстве.

Свойство 1. Аналогично свойствам двойного интеграла. Для вычисления 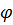воспользуемся формулой дифференциала длины дуги.

dl=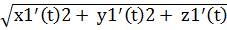

Если l: x=x(t), y=y(t), z=z(t), t 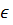[t₁;t₂] , то 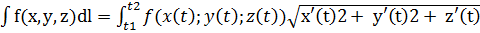dt

На плоскости формула аналогична.

Если на плоскости y=f(x), x 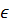[a;b], то параметрически ее можно расписать x=x; y=f(x) x 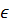[a;b]

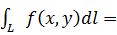
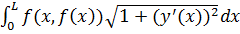
Приложение 3.1.

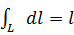--длина L

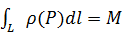-- масса точки L