Ряды с положительными членами

Понятие ряда.

Выражение

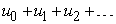, (1)

где числа 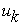(члены ряда), вообще комплексные, зависят от индексов 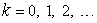, называется рядом. Этому выражению мы не приписали никакого числа, потому что сложение бесконечного числа слагаемых не имеет смысла. Ряд (1) еще записывают так:

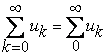. (2)

Это чисто формальная запись часто более удобна, чем запись (1).

Числа

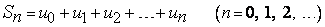
называются 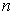-ми частичными суммами ряда (1).

По определению ряд (1) сходится, если существует

.

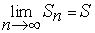В этом случае пишут

(3)

и называют 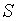суммой ряда, т. е. выражениям (1) или (2) приписывается число 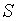. Говорят еще, что ряд (3) сходится к .

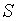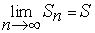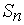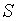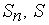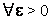
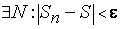
З а м е ч а н и е. Равенство , где и - комплексные, определяется так же, как для действительных , т. е. оно обозначает, что 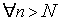. Здесь 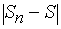- модуль разности двух комплексных чисел 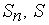. Для комплексных переменных доказывается в точности так же, как для действительных переменных, что предел суммы, разности, произведения и частного переменных 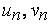равен соответственно сумме, разности, произведению частному пределов этих переменных с обычной оговоркой в случае частного .

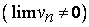В силу условия Коши (верного и для последовательностей комплексных чисел), для того чтобы ряд (1) сходился, необходимо и достаточно, чтобы для всякого 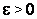нашлось такое 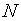, чтобы для всех натуральных 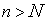и любого натурального 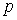выполнялось неравенство

.

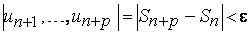Отсюда в частности (полагая ), следует, что если ряд (1) сходится, то его общий член стремится к нулю:

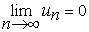. (4)

Но условие (4), будучи необходимым, не является достаточным для сходимости ряда, как это будет видно из дальнейших примеров.

Рассмотрим еще ряд

(5)

Так как условие Коши сходимости рядов (1) и (5) формулируется совершенно одинаково, то они одновременно либо сходятся, либо расходятся (не сходятся). Если они сходятся, то сумма ряда (5) равна

.

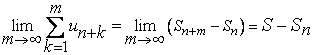Ряд (5) называют остатком или остаточным членом ряда (1).

Если члены ряда (1) неотрицательны (таким образом, действительны), то его частичные суммы образуют неубывающую последовательность 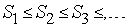, поэтому, если эта последовательность ограничена

,

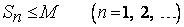то ряд сходится и его сумма удовлетворяет неравенству

.

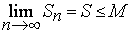Если же она неограниченна, то ряд расходится:

.

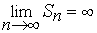В этом случае пишут

.

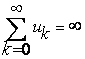Пример. Ряд

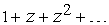(6)

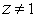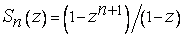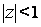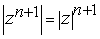имеет (при ) частичную сумму . Если , то и 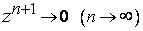. Таким образом, ряд (6) сходится и имеет сумму, равную 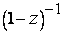- на открытом круге 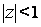. Если же 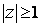, то ряд (6) расходится, потому что в этом случае его общий член, имеющий модуль, не меньший единицы , не стремится к нулю при .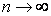

Решение.

Радиус сходимости степенного ряда можно найти по формуле: .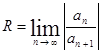

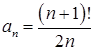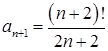Т.к. и , то

.

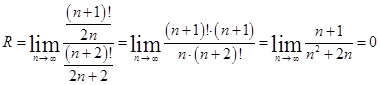Итак, радиус сходимости ряда 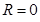. Т.о. данный степенной ряд расходится, при .

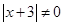Исследуем сходимость ряда при .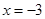

Пусть 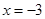. Подставим 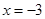в заданный степенной ряд и получим ряд

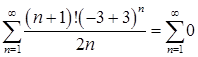, который сходится.

Итак, областью сходимости данного степенного ряда является значение .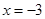

Пример2:

Найти область сходимости степенного ряда .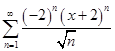

Решение.

Радиус сходимости степенного ряда можно найти по формуле: .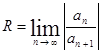

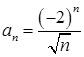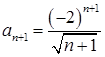Т.к. и , то

.

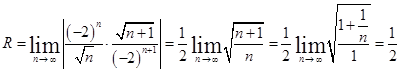Итак, радиус сходимости ряда 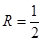. Определим интервал сходимости данного степенного ряда:

.

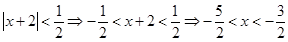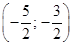– интервал сходимости степенного ряда. Исследуем сходимость ряда на концах интервала сходимости.

Пусть 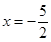. Подставим 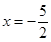в заданный степенной ряд и получим числовой ряд с положительными членами:

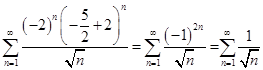
Получили расходящийся обобщенный гармонический ряд .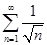

Значит, 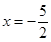не принадлежит области сходимости степенного ряда.

Пусть 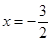. Подставим 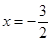в заданный степенной ряд и получим знакочередующийся ряд

.

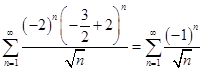Для членов полученного ряда:

1)

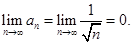
2) 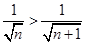, т.е.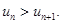

В соответствии с признаком Лейбница данный ряд сходится и 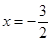принадлежит области сходимости степенного ряда.

Итак, областью сходимости данного степенного ряда является промежуток .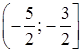

Ряды Фурье.

Ряд Фурье периодических функций с периодом 2π.

Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны - это типичные практические примеры применения периодических функций в инженерных расчетах.

Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):

Стандартная (=обычная) запись через сумму sinx и cosx

f(x)=a_o+ a₁cosx+a₂cos2x+a₃cos3x+...+b₁sinx+b₂sin2x+b₃sin3x+...,

где a_o, a₁,a₂,...,b₁,b₂,.. - действительные константы, т.е.

(1)

Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:

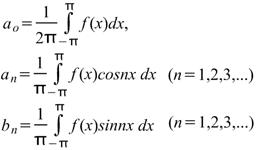
Коэффициенты a_o,a_n и b_n называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a₁cosx+b₁sinx) называется первой или основной гармоникой,

Другой способ записи ряда - использование соотношения acosx+bsinx=csin(x+α)

f(x)=a_o+c₁sin(x+α₁)+c₂sin(2x+α₂)+...+c_nsin(nx+α_n)

Где a_o - константа, с ₁=(a₁²+b₁²)^1/2 , с _n=(a_n²+b_n²)^1/2- амплитуды различных компонент, а фазовый угол равен a_n=arctga_n/b_n.

Для ряда (1) член (a₁cosx+b₁sinx) или c₁sin(x+α₁) называется первой или основной гармоникой,(a₂cos2x+b₂sin2x) или c₂sin(2x+α₂) называется второй гармоникой и так далее.

Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.

Ряд Фурье непериодических функций с периодом 2π.

Четные и нечетные функции.

Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х² и у=cosx.

Говорят, что функция y=f(x) нечетная,если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.

Ряд Фурье на полупериоде.

Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.

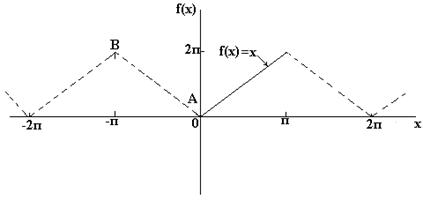
Если требуется получить разложение Фурье на полупериоде по косинусамфункции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ.на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье a_o и a_n

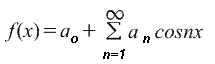
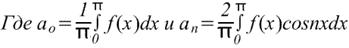
Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b

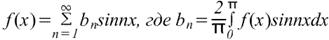
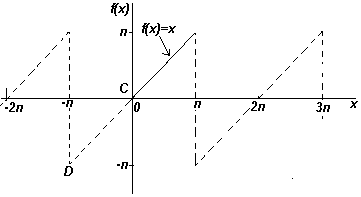
Пример 3.

Найти все решения дифференциального уравнения .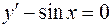

Интегрируя, получим .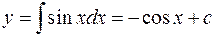

Общим решением дифференциального уравнения называют решение, которое существенно зависит от произвольной постоянной с. Общее решение, полученное в неявном виде называется общим интегралом дифференциального уравнения.

y = - cos x +c – общее решение.

y + cos x = с – общий интеграл.

Решение дифференциального уравнения, которое получается из общего решения при фиксированном значении постоянной c , называют частным решением.

Пусть М(0,2), с= 2+ сos(0); с = 3. y = -cos x + 3 – частное решение, то есть мы выделяем кривую, которая проходит через точку (0,2).

Кривые y = - cos x +c называются интегральными кривыми дифференциального уравнения .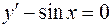

Уравнение вида F(x,y, 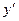)=0 (1) называется дифференциальным уравнением первого порядка.

Задача Коши для дифференциального уравнения первого порядказаключается в отыскании решения уравнения (1), удовлетворяющего начальному условию 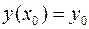. Геометрически это означает определение интегральной кривой, проходящей через точку .

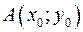Теорема Пикара. Если в уравнении 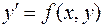функция 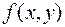определена и непрерывна в окрестности точки 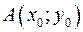и, кроме того, имеет частную производную 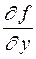, то задача Коши имеет единственное решение, являющееся дифференцируемой функцией. Если в точке 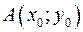условия теоремы Пикара нарушаются, то задача Коши может иметь несколько решений или не иметь их вовсе. В первом случае через точку 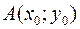проходит несколько интегральных кривых. Точки, в которых происходит нарушение условий теоремы Пикара, называют особыми. Дополнительные решения задачи Коши, возникающие при этом, также называют особыми.

Кратные интегралы.

Двойные интегралы

Определение двойного интеграла и критерий интегрируемости

Определение двойного интеграла:

Мы будем рассматривать функции 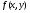, определённые на квадрируемом (то есть имеющем площадь) множестве 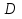. Практически всегда представляет собой фигуру, ограниченную кусочно-гладкой кривой, или конечное объединение таких фигур. Далее, говоря о квадрируемом множестве, мы ограничиваемся рассмотрением именно таких множеств.

Если вспомнить теорию определённого интеграла, то мы начали её изложение с понятия разбиения 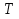отрезка 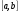. По аналогии, определим разбиение квадрируемого множества , как представление множества в виде объединения конечного числа квадрируемых частей, .

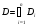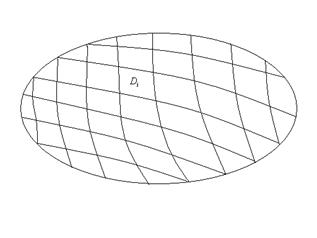
Можно считать, что разбиение на части 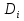также осуществляется с помощью спрямляемых(т.е. имеющих длину) кривых, то есть все также являются фигурами с кусочно-гладкими границами, либо конечными объединениями таких фигур.

В одномерном случае мы рассматривали длины частей разбиения 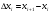. В двумерном случае обобщением понятия длины 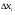будет площадь . Однако нам потребуется также понятие диаметра множества 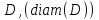. Эта величина определяется, как точная верхняя грань расстояний между точками множества . В частности, если – круг, то 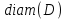– это как раз длина диаметра круга в обычном смысле. В общем понятие диаметра множества поясняет рисунок:

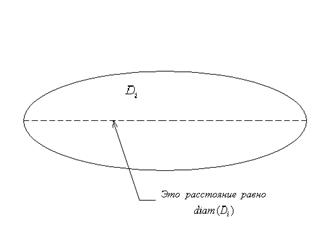
Ясно, что если 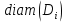невелик, то и площадь также невелика, поскольку неравенство 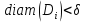означает, что содержится некотором в круге радиуса 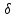и имеет площадь не больше, чем .

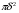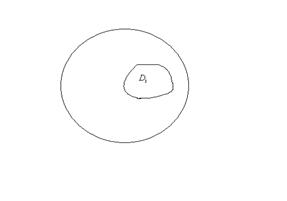
Действительно, возьмём произвольную точку множества в качестве центра этого круга. Так как , остальные точки лежат внутри круга.

Однако площадь множества может быть невелика, а достаточно велик. Пример – очень тонкий прямоугольник.

Определим диаметр 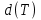разбиения T как наибольший из диаметров частей этого разбиения. Далее, как и в одномерном случае, выберем точки 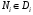(было: 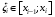).Пусть 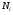имеет координаты 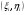. Важную роль в дальнейшем будет играть понятие интегральной суммы, определяемой равенством 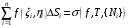. Так же, как и в одномерном случае, эта величина имеет простой геометрический смысл. Вспомним, что сумма 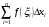представляла собой площадь ступенчатой фигуры вида:

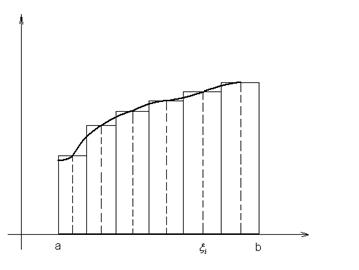
(для простоты считаем, что ).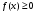

Напомним, что объём цилиндра с основанием, имеющим площадь 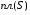и с высотой 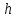равен 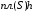. Поэтому интегральная сумма 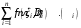равна объёму тела, состоящего из цилиндров с высотой 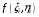(для простоты считаем, что 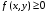) и основаниями .

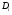Перейдём к основному определению.

Определение.Пусть 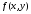- ограниченная на квадрируемом множестве функция. Пусть 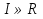. Если

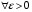
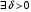
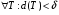
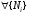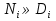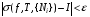_, , , (1)

то будем говорить, что f – интегрируемая на функция и что число 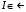является её интеграломна этом множестве. Используется обозначение .

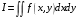Иногда используют обозначение .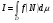

Замечание.Это определение несколько отличается от определения обычного определённого интеграла, в котором отсутствовало требование ограниченности функции 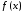. Дело в том, что для обычного определённого интеграла из выполнения условия (1) следовало необходимое условие интегрируемости: если 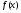интегрируема на , то ограничена на .

Для двойного интеграла из выполнения условия (1) не следует, что функция ограничена. Это условие, например, заведомо выполняется для любой определённой на множестве функции, если множество имеет равную нулю площадь. Для того, чтобы у двойного интеграла сохранились все важные свойства определённого интеграла и добавлено требование ограниченности функции.

Критерий интегрируемости

Критерий существования определённого интеграла 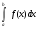формулировался в терминах сумм Дарбу, т.е. сумм вида 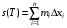, , 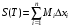где 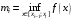, , 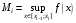то есть 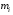- нижняя грань, а 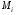- верхняя грань значений при .

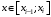Рассуждая аналогично, рассмотрим для ограниченной на квадрируемом множестве функции 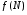числа 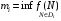, 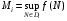(эти числа существуют ввиду предполагаемой ограниченности функции на и, значит, на всех. Определим суммы Дарбу равенствами 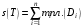, 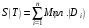. Эти величины представляют собой объемы тел, состоящих из цилиндров с основаниями и высотами, соответственно, 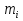и 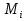. Ясно, что для любого разбиения при любом выборе точек 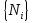выполнены неравенства между суммами Дарбу и интегральной суммой, соответствующей этому выбору точек: .

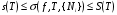На рисунке изображены тела, объёмы которых равны суммам Дарбу.

Нижняя сумма Дарбу

Верхняя сумма Дарбу

Вполне аналогично одномерному случаю можно доказать критерий существования двойного интеграла.

Теорема 1.1.Ограниченная на квадрируемом множестве функция интегрируема тогда и только тогда, когда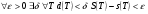

(На экзамене ограничиваемся формулировкой).

Из этого критерия следует теорема.

Теорема1.2.Если функция непрерывна на квадрируемом множестве , то интегрируема на этом множестве.

(На экзамене достаточно формулировки).

Свойства двойных интегралов

Свойство 1. Если 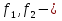- интегрируемые на квадрируемом множестве функции, а 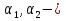числа, то

.

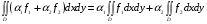Иными словами, интеграл - линейный функционал.

Свойство 2. Если 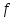- интегрируема на объединении квадрируемых множеств 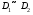, то

,

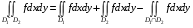причем если площадь пересечения 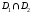равна 0, то 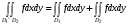. (Аддитивность интеграла по множеству).

Свойство 3.Если- интегрируемая на квадрируемом множествефункция и 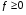, то .

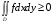Свойство 4.Если - интегрируемые на квадрируемом множестве функции и 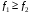, то .

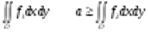Свойство5.Если- интегрируемая на квадрируемом множествефункция , причем .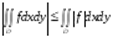

Свойство 6.Если- интегрируемая на квадрируемом множествефункция , то функция 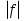– также интегрируемая, причем 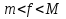где т, М ограничивающие множество значений функции числа, товыполняются неравенства ,

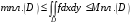т.е.существует число 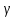, удовлетворяющее неравенствам 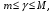для которого

.

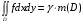Если, кроме того, множество – связное* и- непрерывна на нём,то существует точка 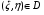, для которой

.

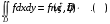Доказывать эти свойства мы не будем, поскольку их доказательства вполне аналогичны доказательствам свойств обычного интеграла.

В конце п.1.2. отмечено, что если -непрерывная на множестве функция, то - интегрируема на . Свойство 2 позволяет утверждать, что если имеет разрывы налишь вдоль конечного числа спрямляемых линий, разбивающихна квадрируемые области, то - интегрируема на , т.к., по свойству 2, интеграл по есть просто сумма конечного числа интегралов по полученным частям (на которых непрерывна и, значит, интегрируема).

*Примечание.Связным множеством на плоскости назовем такое множество, любые две точки которого можно соединить кусочно-гладкой кривой, лежащей в этом множестве.

3. Вычисление двойного интеграла сведением к повторному интегралу

Двойной интеграл – новый объект и мы укажем способ его вычисления сведением к повторному вычислению определённого интеграла. Сначала рассмотрим двойной интеграл по прямоугольной области 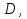стороны которой параллельны осям координат.

Теорема 1.3.Пусть для функции 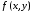существует двойной интеграл 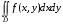по области 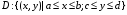. Кроме того, пусть для любого 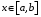существует .

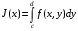Тогда существует и интеграл, называемый повторным:

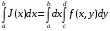
и выполняется равенство

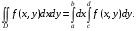(2)

►Разобьём прямоугольник на прямоугольники, обозначенные 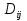, прямыми, проходящими параллельно оси 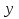через точки 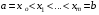и прямыми, параллельными оси 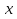и проходящими через точки 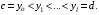Таким образом,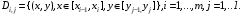

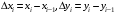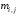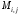Пусть , числа и , соответственно, равны нижней и верхней граням функции 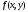на 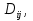откуда 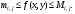Проинтегрируем эти неравенства по на отрезках :

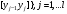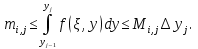
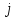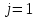Суммируя эти неравенства по от до 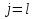, получаем

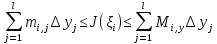
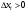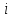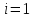Умножим все части этих неравенств на и суммируем полученные неравенства по от до :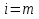

.

Поскольку 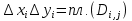, эти неравенства можно переписать в виде

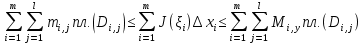
или

,

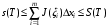где – разбиение на прямоугольник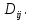и При 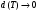стремится к нулю и величина 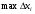. Кроме того, при также 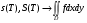. Значит, интеграл 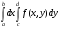существует и равен , что и утверждалось.◄

Замечания.

1. В случае, когда непрерывна навсе условия теоремы выполняются и равенство (2) справедливо.
2. Отметим, что интеграл 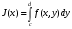представляет собой собственный интеграл, зависящий от параметра.

Рассмотрим случай криволинейной трапеции. Справедлива такая теорема:

Теорема 1.4 (Фубини).Пусть область задана неравенствами 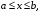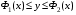, где 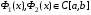. Пусть существует 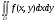и для любого существует 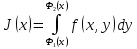. Тогда существует интеграл 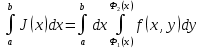и он равен .

►Так как 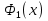непрерывна на 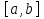, существует её минимальное значение 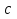на этом отрезке. Аналогично, существует максимальное значение 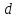функции 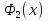на отрезке 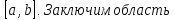в прямоугольник 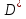, состоящий из точек 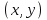, , 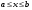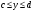. На этом прямоугольнике рассмотрим функцию

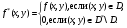
Условия предыдущей теоремы для функции 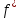выполнены. Она интегрируема в , равна 0 (и, значит, интегрируема) в 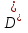. Следовательно, она интегрируема на всём множестве . При этом

.

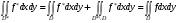Наконец, для любого 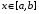выполнено равенство

.

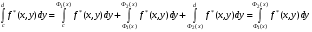По доказанному в предыдущей теореме,

,

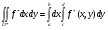откуда сразу получаем:

,

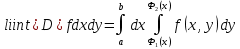что и требовалось доказать.◄

Следствие: Пусть ) непрерывна в области , ограниченной сверху графиком функции 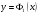, снизу - , где , a по бокам - отрезками вертикальных прямых х = а и х = b. Тогда

.

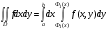►Из непрерывности 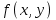сразу следует её интегрируемость на . Кроме того, для любого 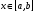функция непрерывна (а, значит, интегрируема по у). Все условия теоремы выполнены. ◄

Замечание. Если область можно ограничить так:
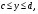
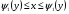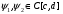, , то

.

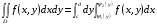Смысл этих теорем ясен – указан способ сведения двойного интеграла к собственным интегралам, зависящим от параметра.

Тройные интегралы

Рассмотрим кубируемое множество 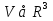. Считаем, что оно ограничено конечным числом кусочно-гладких поверхностей . Разбиение на части 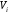также осуществляется кусочно- гладкими поверхностями. Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции 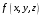, разбиения множества 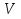на части и для выбранных точек 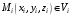интегральную сумму

,

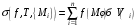где 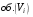обозначает объем части .

Определение. Пусть такое число, что .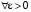

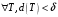
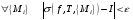Тогда мы говорим, что функция интегрируема на множестве , число есть интеграл функции по множеству и обозначаем это так: .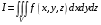

Как и в случае двойного интеграла, выполняются свойства 1-6. Полезное упражнение - переформулировать их для тройного интеграла .

Теорема 2.1. Ограниченная на кубируемом множестве функция 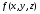интегрируема тогда и только тогда, когда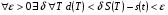

(На экзамене ограничиваемся формулировкой).

Из этого критерия следует теорема.

Теорема 2.2. Если функция непрерывна на кубируемом множестве , то интегрируема на этом множестве.

(На экзамене достаточно формулировки).

Точно также можно убедиться в том, что если точки разрыва лежат на конечном числе кусочно-гладких поверхностей, лежащих на и разбивающих на кубируемые области, то интегрируема на .

Вычисление тройного интеграла производится по следующему правилу.

Теорема 2.3.Пусть задана следующими неравенствами:

,

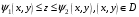где — квадрируемая область на плоскости, 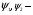непрерывные функции. Тогда

.

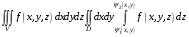Замечание. Если область задана неравенствами 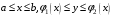, где 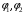— непрерывные функции, то

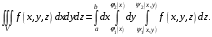
Сформулируем общую теорему о замене переменных.

Теорема 2.4. Пусть отображение 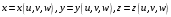устанавливает взаимно однозначное соответствие между областям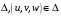и и 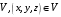, причем функции 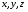— непрерывно дифференцируемые и ни в одной точке 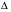.Пусть всюду в области

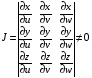
Пусть — непрерывная функция. Тогда

.

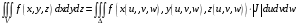Как и для двойного интеграла, теорема остается верной в случае нарушения ее условий на множестве нулевого объема.

Пример 1. Переход к цилиндрическим координатам. Он осуществляется с помощью функций: .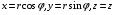

При этом якобиан равен

.

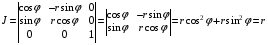Пример 2. Переход к сферическим координатам осуществляется функциями .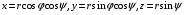

Якобиан преобразования равен

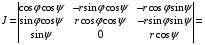
(разложение определителя по 3-й строке)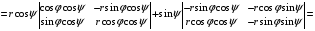

(выделение общих множителей у столбцов)

.

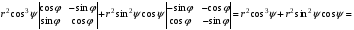
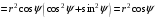Часто используется интеграл (вы встретите его при вычислении двойных, тройных интегралов при переходе к сферическим или цилиндрическим координатам)

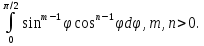
Сведем его к значен