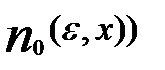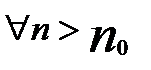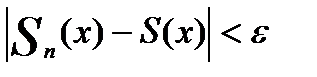Признаки сходимости рядов с неотрицательными членами

Если дан ряд 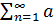_n c неотрицательными членами, то последовательность его частичных сумм является неубывающей. Необходимы и достаточным признаком такой последовательности является ее ограниченность. Отсюда следует

Теорема1. Для того чтобы ряд с неотрицательными членами сходился необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.

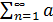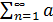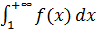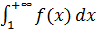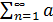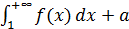Теорема2. Интегральный признак. Если неотрицательная интегрируемая на промежутке от 1 до +∞ функция f(x) монотонно убывает и члены ряда _n имеют вид a_n=f(n) то ряд _n и сходятся или расходятся одновременно, причем в случае сходимости ≤ _n ≤ _n

Теорема3. Признак сравнения. Если для ряда 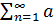_n и 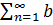_n с неотрицательными членами выполняется неравенство a_n≤b_n для любого nϵN , то из сходимости 2ого ряда следует сходимость 1ого, а из расходимости 1ого следует расходимость 2ого.

Док-ва: Пусть 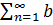_n=b

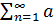_n=a

Сумма 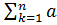_k=S_k , 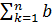_k=S_n′

1) Если 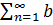_n сходится, то (S_n) ограничена и поэтому ряд 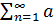_nc_x cходится.

2) Если 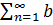_n расходится то S_ni′ неограниченa =› S_u′-неограненa =› 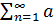_n –расходится.

Теорема4. Предельный признак сравнения. Если для знакоположительных рядов 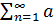_n и 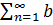_n существует конечный предел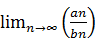 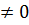, то ряды сходятся или расходятся одновременно.

Замечание: для того чтобы применить m3 и m4 нужно догадаться с каким рядом сравнивать. Обычно этот ряд из членов геометрической прогрессии или ряд Дирихле. Ряд Дирихле выбирают из дробей с наивысшими степенями неизвестной числителя и знаменателя.

Теорема5. Признак Даламбера. Если для знакоположительного ряда 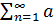_n существует

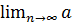_n+1/ 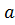_n =L, то при L 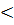1 рад сходится, а при L 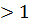ряд расходится

Замечание: При L=1 теорему 5 применить нельзя.

n!=1∙2∙3∙4∙…∙n 0!=1.; 1!=1∙1=1; 2!=1∙2=2

Теорема6. Признак Коши. Если для знакоположительного ряда 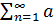_n существует предел 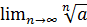_n , то при L 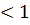ряд сходится, при L 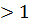ряд расходится.

Замечание.Можно показать, что если существует предел 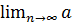_n+1/ 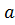_n , то существует 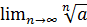_n и они равны. Обратное утверждение не всегда имеет место. Значит признак Коши сильнее признака Даламбера.

Знакопеременные ряды. Абсолютные и условные сходимости. Признак Лейбница.

Знакопеременный ряды – ряды, с членами разных знаков.

Пусть дан ряд 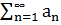рассмотрим знакоположительный ряд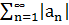

Теорема1. Если ряд 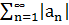сходиться, то 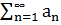- сходиться.

По свойствам сходимости рядов ряд 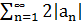– сходиться, т.к. для любого nЄN, 0 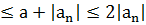, то по признаку сравнения ряд 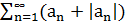- сходиться.

Значит ряд 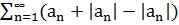- сходиться.

Т.1. даёт достаточный признак сходимости, который не является необходимым. В связи с этим сформулируем определение 1:

· если ряд 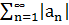- сходиться, то говорят что ряд 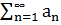- сходиться абсолютно.

· если же ряд 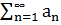- сходиться, а ряд 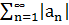- расходиться, то говорят что 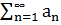сходиться условно.

Знакочередующиеся ряды

Опр.2 Ими называют - ряды, члены которых поочередно меняют знак: a₁-a₂+a₃-…

Где a₁,a₂,a₃…. – одного знака. Удобно применять запись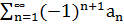

Признак Лейбница

Знакочередующийся ряд ( знаки членов которого строго чередуются) сходиться если:

1) Члены его убывают по абсолютному значению т.е. .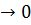

2)

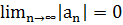
Замечание:

Признак Лейбница является достаточным, но не является необходимым.

Следствие 2.1

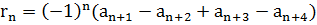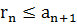; ; Остаток не превышает по модулю первый из отброшенных членов.

Действительно остаток r_n представляет собой ряд Лейбница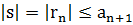

Функциональные ряды

Определение . 1

Пусть 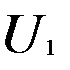(X), 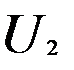(x)… последовательность функций, определ-ых на некотороемножество X. Выражение вида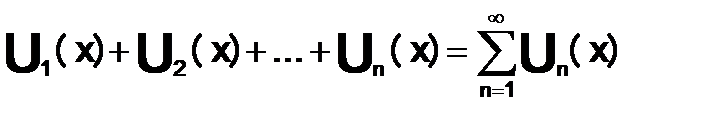назыв. — функциональным рядом.

Каждому значению 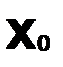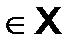соответствует числовой ряд 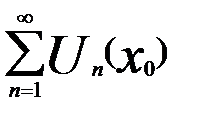, если последний ряд сходится, то 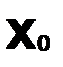назыв.—точкой сходимости.

Множество всех точе сходимости функционального ряда назыв.— областью сходимости.

Конечная сумма 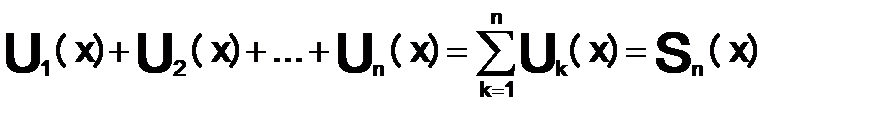—n-ая частичная сумма ряда.А функция S(x)= 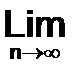S(x) — суммой ряда.

Область определения D(S(x)) — область сходимости.

Функция 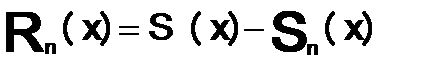определенная на множестве D(S(x))назыв. — n-ый остаток ряда.Сходимость ряда в точке назыв. — поточечной.

Функциональный ряд 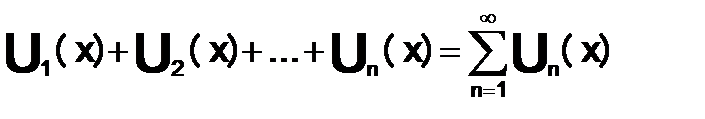назыв. — абсолютно сходящимся на множестве 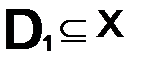, если 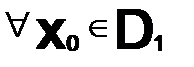, ряд 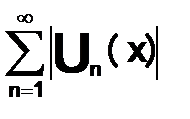то такой ряд сходится.

Опред. 2

Функциональный ряд 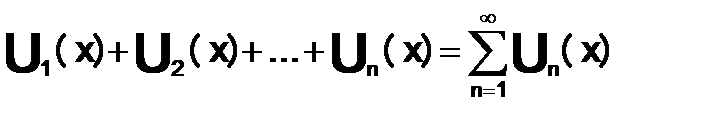назыв. — равномерно сходящимся в области D функции S(x), если , , .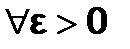

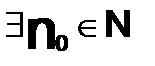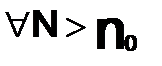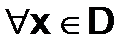
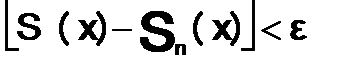Отличие равномерной сходимости от поточечной в том, что номер 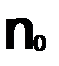при равномерной сходимости зависит только от 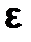и не зависит от X.А при поточечной сходимости 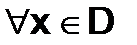номер 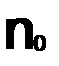свой.

Поэтому из равномерной сходимости следует поточечная.

Дадим определение поточечной сходимости области ряда D.

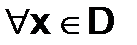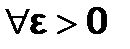
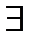
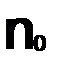
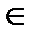, N(