Теорема 1. Признак ВЕЙЕРШТРАССА

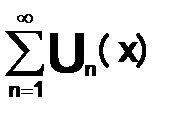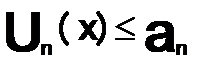
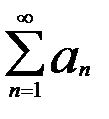Если члены ряда удовлетворяет неравенство , а ряд — сходится, то функциональный ряд 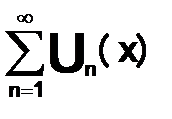— сходится равномерно в области D.

Числовой ряд 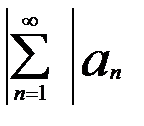из Теоремы 1 назыв. — мажорантым для функционального.

Теорема 2. О Непрерывности суммы равномерно сходящегося ряда.

Если функциональный ряд 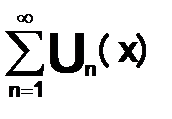с непрерывными членами сходится равномерно на множестве D,то его сумма S(x)непрерывна на множестве D.

Следствие 2.1

В равномерно сходящемся ряде с непрерывно сходящимися членами возможен переход к пределу, т.е.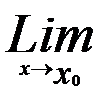

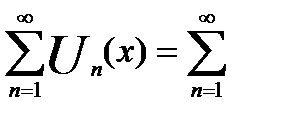
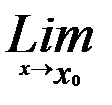
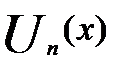
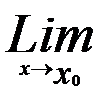
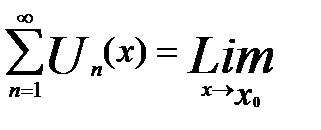S(x)=S(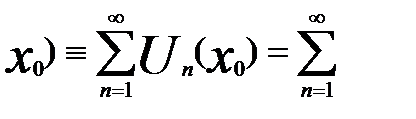

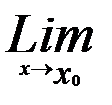
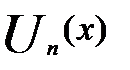
Теорема 3. О почленном дифференцировании функционального ряда.

Если ряд 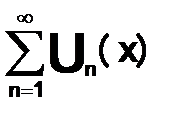с непрерывно дифференцированными на отрезке [a, b] членами сходится функция S(x)на отрезке [a,b], а 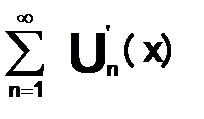сходится равномерно на [a,b], то ряд 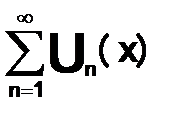можно почленно дифференцировать на любом отрезке [a,b], его сумма S(x)непрерывно дифференцируемая функция и 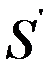(x)= .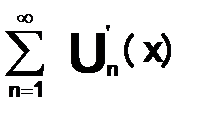

Теорема 4. О почленном интегрировании функциональных рядов.

Если функциональный ряд 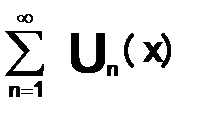сходится равномерно S(x) на [a,b],то его можно почленно интегрировать на любом отрезке [a,b]и справедливо равенство

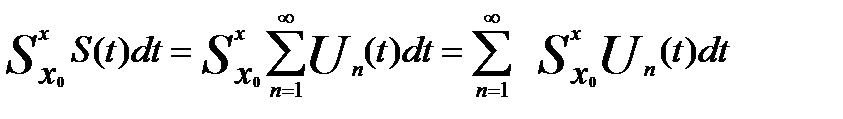
Непрерывность суммы равномерно сходящегося функционального ряда. Почленное интегрирование и дифференцирование функциональных рядов.

Теорема о непрерывности суммы сходящегося функц. ряда:

Если функ-ый ряд 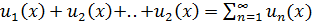(*) с непрерывн. членами сходится равномернов области D, то его сумма непрерывна на D.

Следствие: в равномерно сходящемся ряду с непрерыв. членами возможен переходк пределу: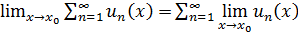

Теорема о почленном интегрировании:

Если функциональный ряд (*) с непрерыв. членами сходится равномерно ф-ции S(x) на [a;b] , то его можно почленно интегрировать на любом отрезке [x₀;x] 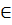[a;b] и справедливо:

Теорема о почленном дифференцировании:

Если ряд (*) с непрерывно дифференцируемыми на [a;b] членами сходится к ф-ии S(x), а ряд 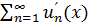– сходится равномерно на [a;b], то ряд (*) сход. Равномерно на [a;b] и его сумма S(x) – непрерывно дифференцируема, причём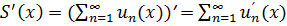

Степенные ряды. Теорема Абеля. Радиус сходимости степенного ряда.

Определение 1

Ряд вида 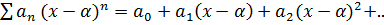, где a_n, x R, наз. степенным рядом по степеням 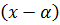. При α=0 получаем ряд 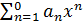(*) по степеням x.

Т.к. 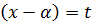любой ряд можно свести к виду (*), то в дальнейшем будем рассматривать только такие ряды. При х=0 степенной ряд (*) сходится.

Теорема Абеля:

Если степенной ряд (*) сходится в т. X₀≠0, то он сходится абсолютно в интервале (-|X₀|;|X₀|) и сходится равномерно на любом отрезке [-q;q], где 0<q< X₀

Определение 2:

Радиус сходимости степенного рядо – это такое число R что ряд сход. в (-R;R) и расходится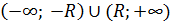

Если ряд сходится только в точке X=0, то R=0. Для нахождения радиуса сходимости используют признак Доламбера и Коши.

Теорема:

Если радиус сходимости степенного ряда ≠0, то его сумма не прерывна в (-R;R)

Теорема:

Операции почленного интегрирования и дефференцирования степ. ряда не меняют его радиус сходимости.

Ряды Тейлора и Маклорена

Пусть функция y=f(x) имеет в окрестности точки х₀ производную любого порядка. Поставим в соответствие степенной ряд f(x) → f(х₀) + f’(х₀) (x- х₀) + 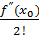(x-x₀)² + 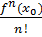(x-x₀)ⁿ+ … = (*)

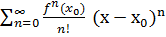Ряд (*) называется рядом Тейлора в окрестности точки х₀ функции f(x).

Если х₀=0 то ряд Тейлора f(x) → f(0) + f’(0)x + 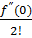x² + 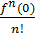xⁿ + … называется рядом Маклорена.

Радиус сходимости степенного ряда (*) может быть =0 или ≠0.

Причем в последнем случае сумма ряда может не совпадать с функцией f(x)

Важно знать S(x) = f(x).

Теорема 1 (Достаточный признак разложимости функций ряда Тейлора)

Если в некоторой окрестности (х₀ –R; х₀ +R) точки х₀ все производные функции f(x) ограничены одной константой, то ряд сходится в функции f(x) в данной окрестности.

При условиях Т.1 ряд Тейлора сходится в функции для которой он составлен.