Замена переменных в кратных интегралах.

1⁰.В одинарном интеграле: .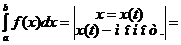

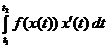2⁰.В двойном интеграле:

.

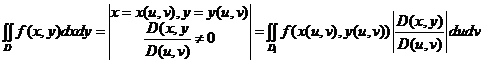3⁰.В тройном интеграле: =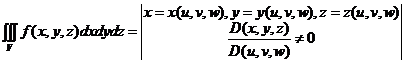

= .

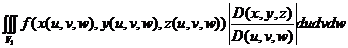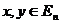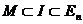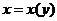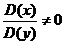4⁰.В кратном интеграле: если , , и , то

.

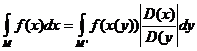Примеры:

1⁰. Вычислить двойной интеграл: .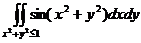

Область интегрирования – круг единичного радиуса с центром в начале координат.

a). В декартовой системе координат: .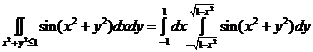

Недостатки: пределы интегрирования не красивые и, кроме того, интеграл не выражается через элементарные функции.

б). В полярной системе координат:

.

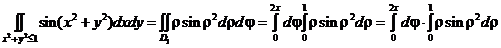При переходе в полярную систему координат не только получился повторный интеграл с удобными пределами интегрирования, но, с учетом того, что внутренний интеграл не зависит от 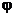получилось даже произведение двух интегралов Римана.

2⁰. Вычислить 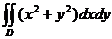, если область D – замкнутая часть плоскости ограниченная кривыми: {y = 2x; y = 4x; xy = 1; xy = 3}.

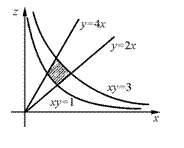a). Расставлять пределы интегрирования в декартовой системе координат

расставлять очень не удобно. Поэтому сделаем по другому.

б). Сделаем замену переменных: u = xy, v = 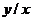; 1 ≤ u ≤ 3, 2 ≤ v ≤ 4.

Для выполнения замены переменных необходимо найти якобиан 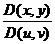. Однако находить его неудобно. Поэтому воспользуемся соотношением: 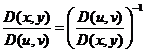. Тогда 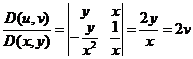. Якобиан положителен, следовательно, ориентация двух систем координат совпадает. И далее:

=…

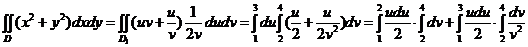3⁰. Вычислить интеграл .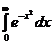

I = 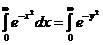Þ 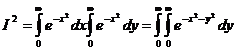. Для нахождения полученного двойного интеграла перейдем в полярную систему координат.

= .

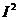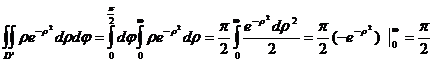
Тогда: 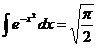. Пример показывает что не только двойной интеграл вычисляется с помощью перехода к повторным, но и наоборот.

§. Криволинейные интегралы 1^го рода.

Def : Если в Е₃ задана вектор-функция 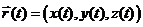, 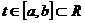и при этом x(t), y(t), z(t) 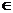C_[a,b], C¹_[a,b] , то говорят, что в Е₃ задана гладкая кривая L.

Пусть на кривой L задана скалярная функция f (x,y,z).

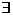Замечание: Если t₁, t₂ такие, что x(t₁) = x(t₂), y(t₁) = y(t₂), z(t₁) = z(t₂), то кривая L имеет самопересечение, но, при этом f (x(t₁), y(t₁), z(t₁)) не обязательно совпадает с f (x(t₂), y(t₂), z(t₂)), поэтому, записывая f (x,y,z) мы будем иметь в виду f (x(t), y(t), z(t)).

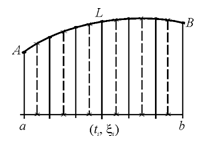
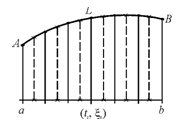
Рассмотрим промежуток [a,b] изменения параметра t , и на [a,b] зададим разбиение P с отмеченными точками ξ, т.е. зададим (P,ξ).

Разбиение (Р,ξ) отрезка [a,b] индуцирует разбиение кривой L с отмеченными точками.

Рассмотрим: 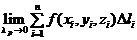, где 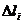– длина хорды, соединяющей концы соответствующего участка кривой. Если такой предел существует и конечен, то он называется криволинейным интегралом 1^го рода , и обозначается .

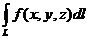Физический смысл криволинейного интеграла 1^го рода – масса кривой L с линейной плотностью масс f (x, y, z).

Для нахождения элемента длины дуги 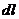будут полезны следующие формулы:

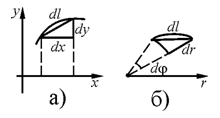
1⁰. Для плоской кривой, заданной в декартовых координатах:

dl = 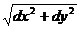(по теореме Пифагора, см. рис. а).

В частных случаях различных способов задания кривой L получаем:

1а. Если y = y(x), то dl = ;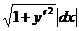

1б. Если x = x(y), то dl = ;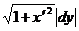

1в. Если x = x(t), y = y(t), то dl = ;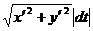

2⁰. Для плоской кривой, заданной в полярных координатах x = ρcosφ, y = ρsinφ:

dl = 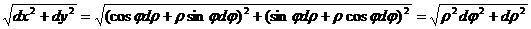. Формула эта может быть получена и непосредственно из криволинейного треугольника (см. рис. б).

2а. Если 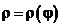, то dl = ;

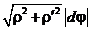2б. Если 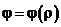, то dl = ;

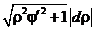2в. Если 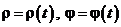, то dl = ;

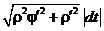3⁰. Для пространственной кривой, заданной в декартовых координатах:

dl = .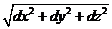

3а. Если 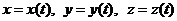, то dl = ;

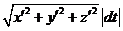4⁰. Если f (x, y, z) = 1 то криволинейный интеграл 1^го рода численно равен длине кривой 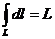и кривая называется спрямляемой.

5⁰. Криволинейный интеграл 1^го рода может быть сведен к обычному интегралу Римана. Пусть 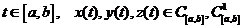. Тогда

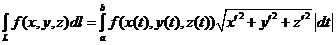. При этом .

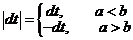Формула следует из определения.

4⁰. Криволинейный интеграл 1^го рода не зависит от направления интегрирования:

.

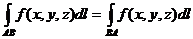Примеры:

1⁰.Вычислить: J= 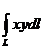, где кривая L: .

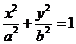Параметрическое уравнение эллипса: 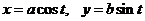Þ

dl = .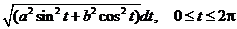

Эллипс пробегается противчасовой стрелки, хотя это указывать не обязательно.

И тогда:

J = = =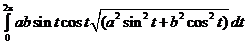

= .

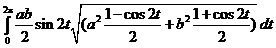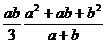2⁰.Найти массу кривой L : y = ln x для 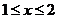, если ρ = x² линейная плотность кривой .

M = =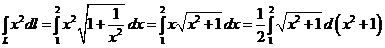

= = .

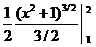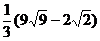3⁰.Найти силу притяжения точки А массы mоднородной полуокружностью радиуса Rс центром в точке А. ( ).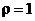

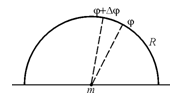Отметим, что сила притяжения это вектор 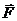, который из соображений симметрии направлен вверх. Найдем F_y (т.к. F_x = 0).

dF_y = 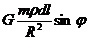, где G – гравитационная постоянная, dl = R dφ; Следовательно: F_y = .

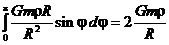§. Криволинейные интегралы 2^го рода.

Def : Пусть в Е₃ задана вектор-функция 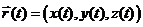, 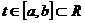и при этом x(t), y(t), z(t) 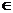C_[a,b], C¹_[a,b] , т.е. в Е₃ задана гладкая кривая L.

Пусть на кривой L задана векторная функция:

.

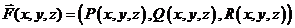Рассмотрим промежуток [a,b] изменения параметра t , и на [a,b] зададим разбиение P с отмеченными точками ξ, т.е. зададим (P,ξ). Разбиение (Р,ξ) отрезка [a,b] индуцирует разбиение кривой L с отмеченными точками. И рассмотрим:

.

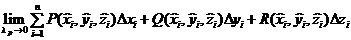Если такой предел существует, то он называется криволинейным интегралом 2^го рода и обозначается: .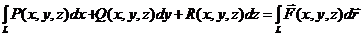

Геометрический смысл криволинейного интеграла 2^го рода – работа силового поля 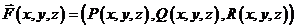вдоль кривой L.

1⁰.Если 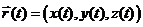, 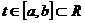и при этом x(t), y(t), z(t) 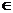C_[a,b], C¹_[a,b] ,

=

= .

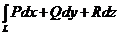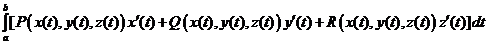Эта формула дает способ вычисления криволинейного интеграла 2^го рода сведением к интегралу Римана, и следует из определения, в котором в левой части фактически записана интегральная сумма для интеграла стоящего в правой части.

2⁰.Формула для вычисления криволинейного интеграла 2^-го рода:

.

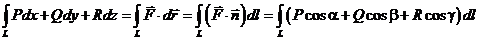Здесь 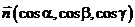– единичный вектор касательной к кривой, а 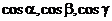– его направляющие косинусы.

3⁰. .

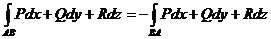4⁰. Формула Грина. Пусть G – плоская область и γ – кусочногладкий контур, являющийся границей области G. Пусть в 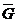заданы P(x,y) и Q(x,y), непрерывные в G вместе с 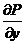и 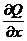. Тогда: .

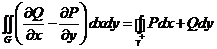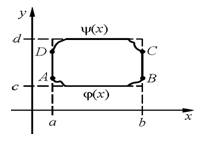Замечание: γ⁺ - означает, что контур γ проходится в положительном направлении – т.е. против часовой стрелки (при обходе контура левая рука все время находится в области.

Δ. Рассмотрим: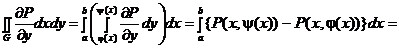

= .

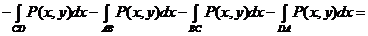
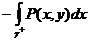Здесь учтено, что интегралы 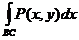и 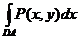равны нулю из-за того, что на промежутках BC и DA .

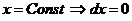Таким образом: 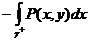= 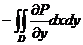. Аналогично: = .

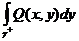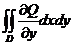После сложения двух полученных формул, получаем доказываемую формулу. ▲

Примеры :

1⁰. Вычислить 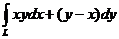, если кривая L соединяет точки от (0,0) до (1,1).

a. y = x ; б. y = x²; в. x = y² .

а). J = .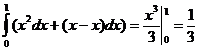

б). J = .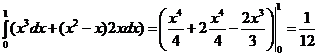

в). J = .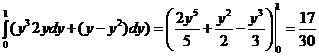

Выясняется, что интегралы получаются разные, т.е. значение интеграла зависит не только от начальной и конечной точек кривой, но и от самой кривой L.

2⁰. Вычислить 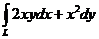вдоль тех же кривых, что и в предыдущей задаче.

a) J = 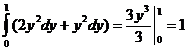. б) J = .

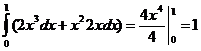в) J = .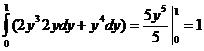

а в данной задаче на всех трех исследованных путях результат один и тот же. Это не означает, что и на других путях так будет, но…

г) Рассмотрим J = .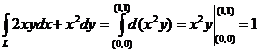

Проведенная выкладка показывает, что интеграл действительно не зависит от пути интегрирования (здесь нет никакого конкретного пути), а зависит только от начальной и конечной точки дуги.

Когда же будет наблюдаться такое явление?

§. Условия независимости криволинейного интеграла 2^го рода

От пути интегрирования.

Т⁰. Пусть функции P(x, y, z), Q(x, y, z), R(x, y, z) определены и непрерывны в

области G , лежащей на гладкой поверхности S, и γ – граница области G.

Тогда эквивалентны следующие условия:

A^*). Для любого замкнутого контура γ в G ;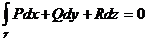

B^*). Для любых A,B є G 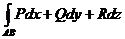не зависит от кривой, соединяющей

точки A и B, и лежащей в области G;

С^*). Выражение Pdx + Qdy + Rdz в G является полным дифференциалом

некоторой функции U(x, y, z), т.е. 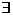U = U(x, y, z) такая,что dU = Pdx+Qdy+Rdz;

D^*). Для функций P(x, y, z), Q(x, y, z), R(x, y, z) в области G выполняются условия:

; ; .

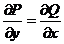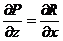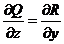При этом : (*)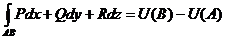

Последнюю формулу можно назвать формулой Ньютона-Лейбница для криволинейных интегралов.

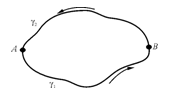
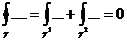
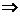
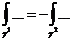
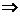
Замечание 1. (связь А^* и В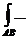^*). не зависит от кривой L, соединяющей точки А и В.

Замечание 2. (связь С^* и D^*).

Если 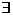U(x, y, z) такая, что ,

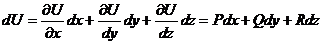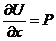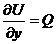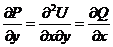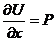
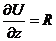то , Þ ;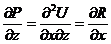

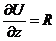
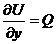Þ ; Þ ^.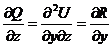

Замечание 3. В случае независимости криволинейного интеграла от пути

интегрирования, 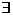U(x, y, z) такая что:

.

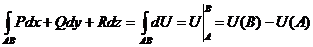Физикиназывают функцию U(x, y, z) потенциалом векторного поля 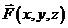, а поле F – потенциальным – “ Работа равна разности потенциалов”.

Математики называют функцию U(x, y, z) первообразной для Pdx+Qdy+Rdz –

интеграл равен разности первообразных в конце и начале пути.

Примеры:

1⁰.Вычислить 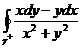для различных контуров γ.

а). Пусть контур γ ограничивающий область G таков, что 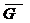не содержит т. (0,0). Для вычисления интеграла воспользуемся формулой Грина.

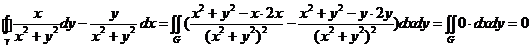где,

, , , .

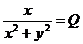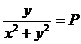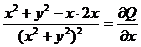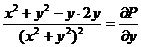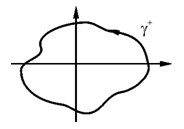
б). Пусть контур γ⁺ окружает точку (0,0). В этом случае нельзя применить формулу Грина ибо 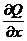и 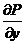в точке (0,0) не существуют.

Отметим, что все интегралы по таким контурам совпадают между собой.

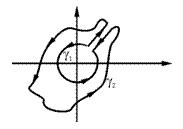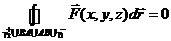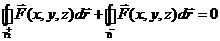Иллюстрация : Þ

Þ .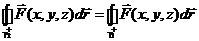

в). Тогда достаточно вычислить 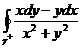скажем, по окружности . .

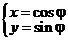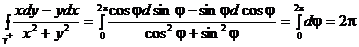г). Легко видеть, что .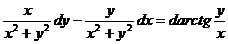

Следовательно, 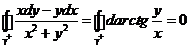, если контур не проходит через точку (0,0) т.к. начальная и конечная точки замкнутого контура совпадают.

2⁰. Найти первообразную, если:

.

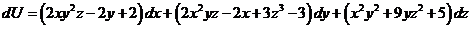Проверка показывает, что условия 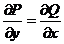; ; 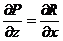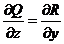выполняются.

Таким образом, задача о нахождении первообразной поставлена корректно. Тогда,

1). 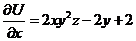и интегрирование по 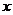дает: .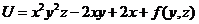

Отсюда 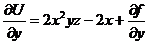. Но 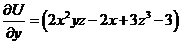из условия задачи.

2). Тогда 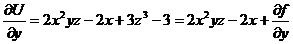Þ .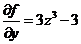

Интегрирование по 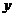дает .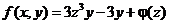

Значит: .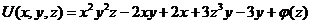

Отсюда 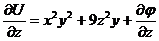. Но из условия задачи .

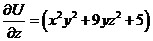3) Тогда 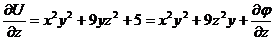Þ .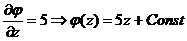

Итог: 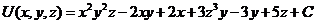. Первообразная найдена с точностью до произвольного постоянного слагаемого. Большего и желать не приходится.