Замена переменных в тройных интегралах

При вычислении тройного интеграла, как и двойного, часто удобно сделать замену переменных. Это позволяет упростить вид области интегрирования или подынтегральное выражение.

Пусть исходный тройной интеграл задан в декартовых координатах x, y, z в области U: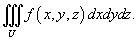

Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями: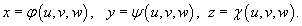

Предполагается, что выполнены следующие условия:

1.Функции φ, ψ, χ непрерывны вместе со своими частными производными;

2. Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;

3. Якобиан преобразования I (u,v,w), равный

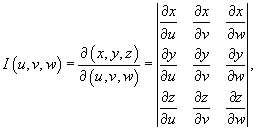
отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.

Тогда формула замены переменных в тройном интеграле записывается в виде:

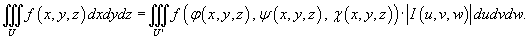
В приведенном выражении 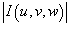означает абсолютное значение якобиана.

Для вычисления тройных интегралов часто используются цилиндрические и сферические координаты. Эти случаи рассматриваются подробно на страницах

- Тройные интегралы в цилиндрических координатах

- Тройные интегралы в сферических координатах

Ниже приводятся примеры вычисления интегралов с использованием других преобразований координат.

Пример 1

Найти объем области U, заданной неравенствами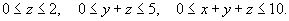

Решение.

Очевидно, что данная область является наклонным параллелепипедом. Удобно сделать такую замену переменных, при которой наклонный параллелепипед преобразуется в прямоугольный. В этом случае тройной интеграл сразу распадается на произведение трех однократных интегралов.

Сделаем следующую замену: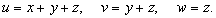

Область интегрирования U' в новых переменных u, v, w ограничена неравенствами

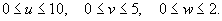
Объем тела равен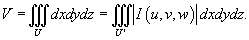

Вычислим якобиан данного преобразования. Чтобы не выражать старые переменные x, y, z через новые u, v, w, найдем сначала якобиан обратного преобразования:

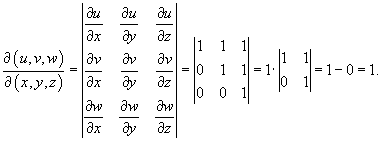
Тогда

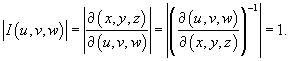
Следовательно, объем тела равен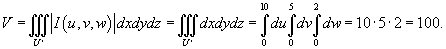

68 Криволинейные интегралы первого рода

Определение

Пусть кривая C описывается векторной функцией 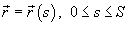, где переменная s представляет собой длину дуги кривой (рисунок 1).

Если на кривой C определена скалярная функция F, то интеграл 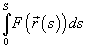называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как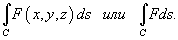

Криволинейный интеграл 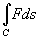существует, если функция F непрерывна на кривой C.

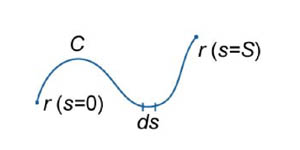
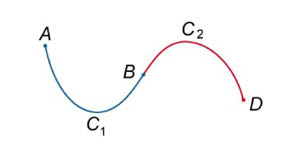
Рис.1 Рис.2

Свойства криволинейного интеграла первого рода

Криволинейный интеграл I рода обладает следующими свойствами:

1. Интеграл не зависит от ориентации кривой;

2. Пусть кривая C1 начинается в точке A и заканчивается в точке B, а кривая C2 начинается в точке B и заканчивается в точке D (рисунок 2). Тогда их объединением будет называться кривая C1 U C2, которая проходит от A к B вдоль кривой C1 и затем от B к D вдоль кривой C2. Для криволинейных интегралов первого рода справедливо соотношение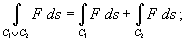

3. Если гладкая кривая C задана параметрически соотношением 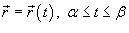и скалярная функция F непрерывна на кривой C, то

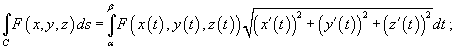
4. Если C является гладкой кривой в плоскости Oxy, заданной уравнением 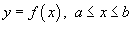, то

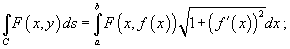
5. Если гладкая кривая C в плоскости Oxy определена уравнением 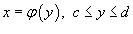, то

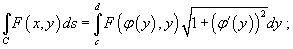
6. В полярных координатах интеграл 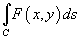выражается формулой

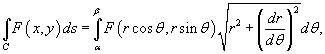
где кривая C задана в полярных координатах функцией .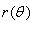

Пример 1

Найти интеграл 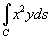вдоль отрезка прямой y = x от начала координат до точки (2,2) (рисунок 3).

Решение.

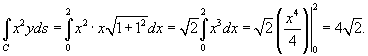
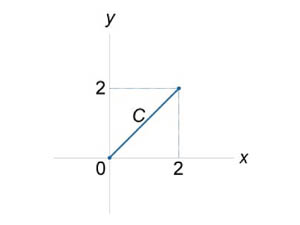
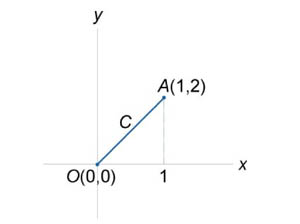
Рис.3 Рис.4