Свойства кратных интегралов.
1°. Линейность: Множество RM функций интегрируемых на множестве М –линейное
пространство, а 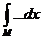 – линейный функционал.
– линейный функционал.
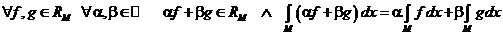 .
.
2°. Условие нормировки: 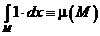 . Другая форма записи
. Другая форма записи 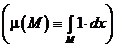 по сути дела определяет меру произвольного множества из евклидового пространства.
по сути дела определяет меру произвольного множества из евклидового пространства.
3°. Если интеграл по множеству Лебеговой меры ноль существует, то он
равен нулю.
Примечание: Множество М называется множеством Лебеговой меры ноль,
если 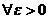
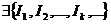 такие, что
такие, что 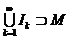 и
и 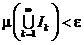 .
.
4°. а. 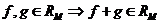 ; б.
; б. 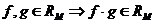 ;
;
в. если 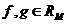 и
и 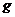 – отделена от нуля на М, то
– отделена от нуля на М, то 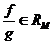
5°. 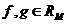 и f = g п.в. (почти всюду) на М, то
и f = g п.в. (почти всюду) на М, то 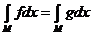 .
.
6°. Аддитивность: Если 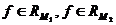 и
и 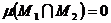 то
то
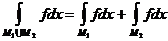 ,
,
В общем случае: 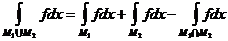 .
.
Δ. Следует из равенства: 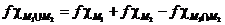 ▲
▲
7°. Монотонность: 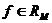 и
и 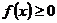 то
то 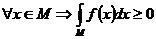 .
.
8°. Интегрирование неравенств: если 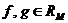 и
и 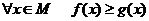 то
то
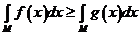 .
.
9°. Пусть 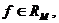
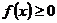
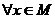 . Для того чтобы
. Для того чтобы 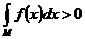 , необходимо и достаточно чтобы существовала внутренняя точка множества М, в которой f (x) > 0 и непрерывна.
, необходимо и достаточно чтобы существовала внутренняя точка множества М, в которой f (x) > 0 и непрерывна.
10°. Интегрируемость модуля интегрируемой функции: 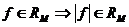 .
.
11°. Теорема о среднем: 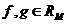 ,
, 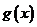 на М сохраняет знак и
на М сохраняет знак и 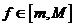 , то
, то
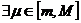
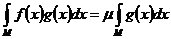 .
.
Если множество М – связно и f (x) – непрерывна на 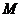 то
то 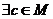 такое, что
такое, что 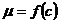 .
.
12°. Для того чтобы интеграл от неотрицательной функции был равен 0
необходимо и достаточно, чтобы f (x) = 0 почти всюду на М.
13°. Теорема Фубини. Для двойного интеграла:
Пусть область 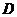 – прямоугольник:
– прямоугольник: 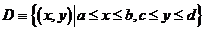 . Тогда, при условии существования внутренних однократных интегралов, для нахождения двойного интеграла можно перейти к повторному интегрированию (см. рис. а):
. Тогда, при условии существования внутренних однократных интегралов, для нахождения двойного интеграла можно перейти к повторному интегрированию (см. рис. а):

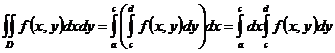 , или
, или
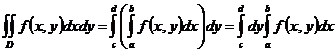 .
.
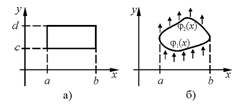 Если область интегрирования не прямоугольник, теорема Фубини все равно справедлива и имеет вид (см. рис. б):
Если область интегрирования не прямоугольник, теорема Фубини все равно справедлива и имеет вид (см. рис. б): 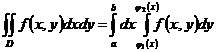 . (*)
. (*)
Примечание:Внешние пределы интегрирования должны быть константами, внутренние пределы интегрирования могут зависеть от переменной, по которой интегрирование ещё предстоит.
Формула (*) может быть получена с использованием характеристической функции множества D.
Для многократного интеграла:
Пусть 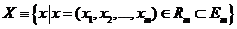 и
и 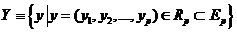 некоторые подмножества евклидовых пространств
некоторые подмножества евклидовых пространств 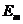 и
и 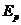 . Определим декартово произведение этих множеств, являющееся подмножеством евклидового пространства
. Определим декартово произведение этих множеств, являющееся подмножеством евклидового пространства 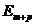 :
: 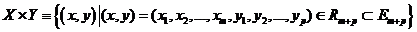 .
.
Тогда теорема Фубини для 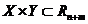 имеет вид:
имеет вид: 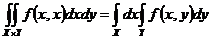 .
.
Теорема справедлива и для брусов X и Y, и для более сложных конфигураций.
Примеры:
10. Вычислить 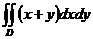 , если граница области
, если граница области 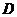 задана уравнениями:
задана уравнениями:
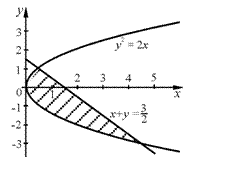
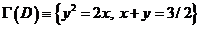
 . Находя точки пересечения кривых определяющих границу области, получаем две точки :
. Находя точки пересечения кривых определяющих границу области, получаем две точки : 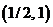 и
и 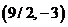 . Тогда возможная расстановка пределов интегрирования при переходе к повторным интегралам дает:
. Тогда возможная расстановка пределов интегрирования при переходе к повторным интегралам дает:
а). 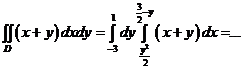 ;
;
б). 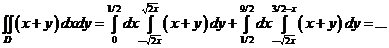 .
.
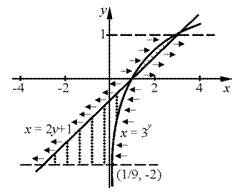 20. Изменить порядок интегрирования в повторном интеграле:
20. Изменить порядок интегрирования в повторном интеграле: 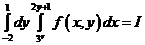 .
.
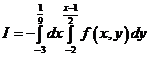 –
–
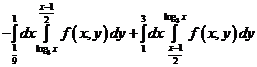 .
.
Рецепт: При расстановке пределов интегрирования в двойном интеграле рекомендуется начинать с внешних пределов интегрирования .
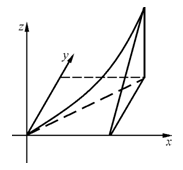 30. Вычислить:
30. Вычислить: 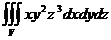 , если
, если 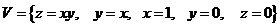
Переход к повторным интегралам даёт: 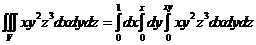 .
.
При этом, в тройном интеграле расстановку пределов надо начинать с внутренних пределов интегрирования. Затем спроецировать область V на плоскость xOy
расставив пределы в области D – лежащей в плоскости xOy.
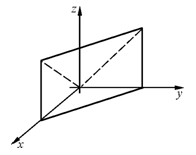
40. Изменить порядок интегрирования в повторном интеграле: 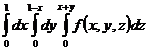 .
.
а). 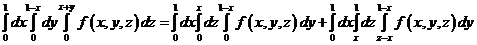 ;
;
б). 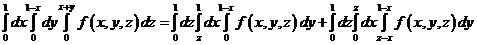 .
.
