Силы давления жидкости на поверхности

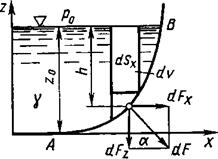
В случае сосуда, наполненного жидкостью и находящегося в покое, любая горизонтальная плоскость в нем является плоскостью равного давления. Поэтому сила полного давления жидкости на горизонтальную площадь 5 определяется по формуле (2.7)

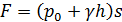
Если внешнее давление равно атмосферному (р₀ = р_ат), то сила давления на горизонтальную площадку .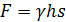

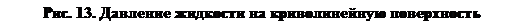По приведенным зависимостям может быть определена сила давления жидкости на плоское дно любого сосуда. В случае наклонной, произвольно ориентированной поверхности, соприкасающейся с жидкостью, сила давления жидкости определяетсяпо приведенным зависимостям, но давление учитывается в центре тяжести рассматриваемой поверхности

,

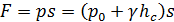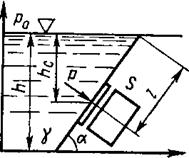
где h_c — вертикальное расстояние центра тяжести стенки от свободной поверхности (рис. 12), h_c = l_Tsinα.

Кроме величины и направления силы давления для расчета сосудов необходимо знать и точку ее приложения (центр давления), которая для произвольно ориентированной площадки определяется по зависимости

,

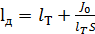где l_д — расстояние от свободной поверхности до центра давления наклонной стенки, измеряемое вдоль наклонной плоскости; J₀ — момент инерции площадки стенки относительно оси, проходящей через центр тяжести площади стенки (см. рис. 12).

Рассмотрим частную задачу для наиболее распространенного типа цилиндрических стенок (рис. 13), ширина которых Вв различных точках по глубине одинакова. Тогда суммарную силу давления удобно разложить на вертикальную составляющую F_z и горизонтальную составляющую F_x, перпендикулярную образующим цилиндра. Если с обратной стороны стенки действует атмосферное давление р_ат, то получим

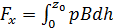, (2.16)

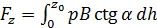, (2.17)

где избыточное давление при р₀ = р_ат

,

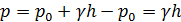а α — угол касательной к стенке на данной глубине к горизонту.

Обозначив площадь вертикальной проекции криволинейной стенки через S_z и учтя, что Bdh = dS_z, hBctgαdh — dV, получим

,

,

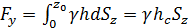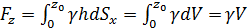где h_c — расстояние центра тяжести площади S_z от свободной поверхности; V — объем тела давления, т. е. объем, ограниченный рассматриваемой криволинейной стенкой, вертикальной цилиндрической поверхностью, проведенной через контур этой стенки и плоскостью свободной поверхности.

Результирующая сила давления жидкости на криволинейную поверхность

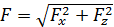(2.18)

и направлена под углом

.

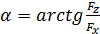Точка приложения равнодействующей сил давления, называемая центром давления, всегда расположена ниже центра тяжести поверхности стенки и может находиться вне этой поверхности.

К рассматриваемым задачам примыкает задача о расчете на прочность тонкостенных цилиндров и труб, находящихся под давлением жидкости.

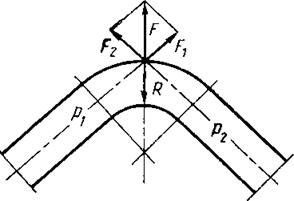
Так, например, при расчете колена трубы (рис. 14), находящейся под внутренним давлением р, исходят из условия

,

.

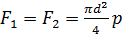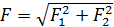Пример 1. Цилиндр диаметром 20 см заполнен водой и закрыт сверху без зазора плавающим поршнем, на поршень положен груз массой о кг. На какую высоту поднимается вода в пьезометре, соединенном -с поршнем?

Подъем жидкости в пьезометре связан с повышением давления зависимостью(2.7)

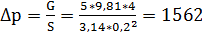Н/м²,

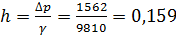м.

Пример 2. Определить давление на дно резервуара и силу давления воды на пробку, закрывающую отверстие в наклонной стенке резервуара (см. рис. 12). Давление на свободную поверхность жидкости р₀= 5 МПа,l= 2 м. Диаметр пробки d = 40 мм.

Абсолютное давление на дно сосуда

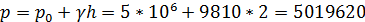Н/м².

Давление на пробку

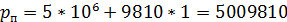Н/м2.

Сила давления жидкости на пробку

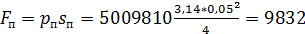Н.

Пример 3. Определить избыточное давление в средней части неподвижного и вращающегося цилиндра, заполненного водой (см. рис. 8). Частота вращения цилиндра n=400 об/мин, D = 600 мм, высотаl=200 мм.

Избыточное давление в неподвижном цилиндре

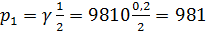Н/м²,

Избыточное давление на стенке вращающегося цилиндра (2.13)

2 g

19,62

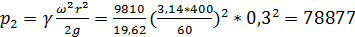Н/м².