Динамика материальной точки и поступательного движения твердого тела

ФИЗИКА

Задания для аудиторных практических занятий и самостоятельной работы студентов

Часть 1

Механика.

Молекулярная физика и термодинамика

Учебное пособие

Ростов-на-Дону

УДК 530.1

Ф 48

Составители: С.И. Егорова

В.С. Ковалева

В.С. Кунаков

Г.Ф. Лемешко

Ю.М. Наследников

Ф 48 Физика: Задания для аудиторных практических занятий и самостоятельной работы студентов. Часть 1.Механика. Молекулярная физика и термодинамика:Учебное пособие. – Ростов н/Д: Издательский центр ДГТУ, 2011. - 56 с.

Цель пособия – обеспечение личностно-ориентированного подхода к практическим занятиям по общему курсу физики с учетом степени подготовки студентов и количества аудиторных часов, выделяемых на лекционные и практические занятия. Пособие предназначено для обучения и контроля работы студентов на практических занятиях по разделу «Механика. Молекулярная физика и термодинамика» в течение первого семестра обучения.

Печатается по решению редакционно-издательского совета Донского государственного технического университета

Научный редактор: д.т.н. проф. В.С. Кунаков

Рецензент:

© Издательский центр ДГТУ, 2011

Общие методические указания

При решении и оформлении задач необходимо соблюдать следующие требования:

1. Записать краткое условие задачи, выразить все известные величины в одной и той же системе единиц (как правило, в СИ). При необходимости ввести дополнительные постоянные физические величины.

2. Решение задач следует сопровождать краткими, но исчерпывающими объяснениями. При необходимости дать чертеж или график.

3. Решать задачу надо в общем виде, выразив искомую величину в буквенных обозначениях, заданных в условии задачи.

4. Произвести вычисления.

В течение семестра студенты выполняют две контрольные работы: первую - по механике, вторую - по молекулярной физике и термодинамике.

Результаты контроля аудиторной и самостоятельной работы студентов на практических занятиях учитываются лектором при приеме экзаменов и дифференцированных зачетов.

Элементы кинематики

Основные формулы и законы

• Средняя и мгновенная скорости материальной точки

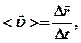
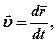
где 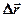- перемещение точки за время 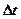, 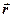- радиус-вектор, определяющий положение точки.

• Для прямолинейного равномерного движения ( )

,

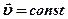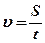где 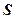– путь, пройденный точкой за время .

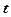• Среднее и мгновенное ускорения материальной точки

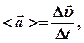
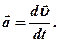
· Полное ускорение при криволинейном движении

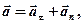
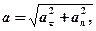
где 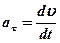- тангенциальная составляющая ускорения, направленная по касательной к траектории; 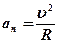- нормальная составляющая ускорения, направленная к центру кривизны траектории ( 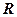- радиус кривизны траектории в данной точке).

· Путь и скорость для равнопеременного движения материальной точки ( )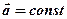

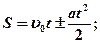
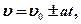
где 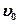- начальная скорость, «+» соответствует равноускоренному движению, «-» - равнозамедленному.

• Угловая скорость

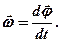
• Угловое ускорение

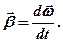
· Угловая скорость для равномерного вращательного движения твердого тела

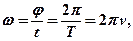
где 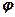- угол поворота тела, 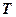– период вращения; 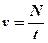- частота вращения ( 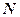– число оборотов, совершаемых телом за время ).

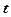· Угол поворота и угловая скорость для равнопеременного вращательного движения твердого тела ( )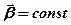

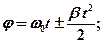
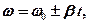
где 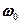- начальная угловая скорость, «+» соответствует равноускоренному вращению, «-» - равнозамедленному.

• Связь между линейными и угловыми величинами:

; ; ;

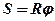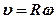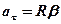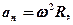
где 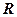– расстояние от точки до мгновенной оси вращения.

ЗАДАНИЯ

1.1. Пароход идет по реке от пункта А до пункта В со скоростью 10 км/ч, а обратно - со скоростью 16 км/ч. Найти: 1) среднюю скорость парохода, 2) скорость течения реки. [12,3 км/ч, 0,83 м/с]

1.2. Скорость течения реки 3 км/ч, а скорость движения лодки относительно воды 6 км/ч. Опреде­лите, под каким углом относительно берега должна дви­гаться лодка, чтобы проплыть поперек реки. [60°]

1.3. Велосипедист проехал первую половину времени своего движения со скоростью 16 км/ч, вторую половину времени — со скоростью 12 км/ч. Определите среднюю скорость движения велосипедиста. [14 км/ч]

1.4. Велосипедист проехал первую половину пути со скоростью 16 км/ч, вторую половину пути — со ско­ростью 12 км/ч. Определите среднюю скорость дви­жения велосипедиста. [13,7 км/ч]

1.5. Студент проехал половину пути на велосипеде со скоростью 16 км/ч. Далее в течение половины остав­шегося времени он ехал со скоростью 12 км/ч, а затем до конца пути шел пешком со скоростью 5 км/ч. Определите среднюю скорость движения студента на всем пути.[11,1 км/ч]

1.6. После удара клюшкой шайба скользит по льду с постоянным ускорением. В конце пятой секунды после начала движения ее скорость была равна 1,5 м/с, а в конце шестой секунды шайба остановилась. С каким ускорением двигалась шайба, какой путь прошла и какова была ее скорость на расстоянии 20 м от начала движения? [1,5 м/c², 27 м, 4,6 м/с]

1.7. Тело, брошенное вертикально вверх, через 3с после начала движения имело скорость 7 м/с. На какую максимальную высоту относительно места броска поднялось тело? Считать 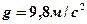. Сопротивлением воздуха пренебречь. [67,6 м]

1.8. Тело падает вертикально с высоты 19,6 м с нулевой начальной скоростью. Какой путь пройдет тело: 1) за первую 0,1 с своего движения, 2) за последнюю 0,1 с своего движения? Считать 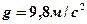. Сопротивлением воздуха пренебречь. [0,049 м, 1,9 м]

1.9. Тело падает вертикально с высоты 19,6 м с нулевой начальной скоростью. За какое время тело пройдет: 1) первый 1 м своего пути, 2) последний 1 м своего пути? Считать 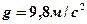. Сопротивлением воздуха пренебречь. [0,4с, 0,05с]

1.10. С башни в горизонтальном направлении брошено тело с начальной скоростью 10 м/с. Пре­небрегая сопротивлением воздуха, определите для мо­мента времени 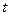= 2 с после начала движения: 1) ско­рость тела; 2) радиус кривизны траектории. Считать 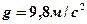. [22 м/с, 109 м]

1.11. Камень брошен горизонтально со скоростью 5м/с. Определите нормальное и тангенциальное ускорения камня через 1 с после начала движения. Считать 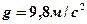. Сопротивлением воздуха пренебречь. [4,45 м/с², 8,73 м/с²]

1.12. Камень брошен горизонтально со скоростью 10 м/с. Найти радиус кривизны траектории камня через 3 с после начала движения. Считать 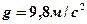. Сопротивление воздуха не учитывать. [305 м]

1.13. Материальная точка начинает двигаться по ок­ружности радиусом 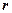= 2,5 см с постоянным тангенциальным ускорением 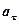= 0,5 см/с². Определите: 1) момент времени, при котором вектор ускорения 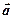образует с вектором скорости 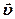угол 45°; 2) путь, пройденный за это время движущейся точкой. [1) 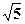с; 2) 1,25 см]

1.14. Линейная скорость точки, находящейся на ободе вращающегося диска, в три раза больше, чем линейная скорость точки, находящейся на 6 см ближе к его оси. Определите радиус диска. [9 см]

1.15. Колесо вращается с постоянным угловым ускорением 3 рад/с². Определите радиус колеса, если через 1 с после начала движения полное ускорение колеса 7,5 м/с². [79 см]

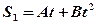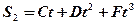1.16. Два автомобиля, выехав одновременно из одного пункта, движутся прямолинейно в одном направлении. Зависимость пройденного ими пути задается уравнения­ми и . Определите закон изменения относительной скорости автомобилей. [ ]

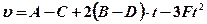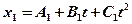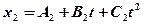1.17. Кинематические уравнения движения двух материальных точек имеют вид и , где 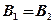, , 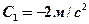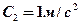. Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения 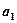и 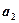для этого момента. [1) 0; 2) - 4 м/с²; 2 м/с²]

1.18. Диск вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением 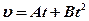( 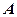= 0,3 м/с², 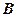= 0,1 м/с³). Определите радиус, если к концу 2 секунды движения вектор полного ускорения образует с вектором скорости угол 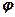= 86°. [0,1 м]

1.19. Нормальное ускорение точки, движущейся по окружности радиусом 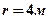, задается уравнением 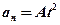, где 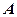= 4 м/с⁴. Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время 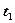= 5 с после начала движения; 3) полное ускорение для момента времени 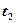= 1 с. [1)4 м/с²; 2)50 м; 3) 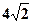м/с²]

1.20. Зависимость пройденного телом пути 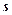от времени 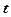выражается уравнением 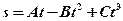( 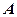= 2 м/с, 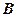= 3 м/с², 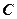= 4 м/с³). Запишите выражения для скорости и ускорения. Определите для момента времени 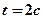после начала движения пройденный путь, скорость и ускорение. [ 24 м; 38 м/с; 42 м/с²]

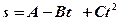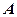1.21. Зависимость пройденного телом пути от времени задаётся уравнением , где =5м, 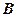=4м/с, 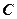=1м/с². Запишите выражения для скорости и ускорения. Определите для момента времени 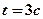после начала движения пройденный путь, скорость и ускорение. [2м; 2м/с; 2 м/с²]

1.22. Зависимость пройденного телом пути от времени задаётся уравнением 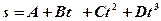, где 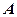=0,1м, 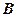=0,1м/с, 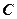=0,14м/с², 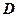=0,01м/с³. 1) Через сколько времени после начала движения ускорение тела будет равно 1м/с²? 2) Чему равно среднее ускорение тела за этот промежуток времени? [1) через 12с; 2) 0,64 м/с²]

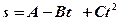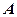1.23. Зависимость пройденного телом пути от времени задаётся уравнением , где =6м, 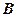=3м/с, 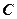=2м/с². Найти среднюю скорость и среднее ускорение в интервале времени от 1с до 4с. [ 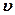=7м/с; 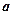=4м/с²]

1.24. Зависимость пройденного телом пути по окружности радиусом 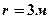задается уравнением 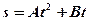( 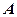= 0,4 м/с², 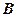= 0,1 м/с). Для момента времени 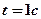после начала движения определите нормальное, тангенциальное и полное ускорения.[0,27 м/с²; 0,8 м/с²; 0,84 м/с²]

1.25. Радиус-вектор материальной точки изменяется со временем по закону 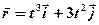, где 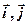- орты осе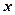й и 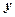. Определите для момента времени 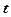= 1 с модуль скорости и модуль ускорения. [6,7 м/с; 8,48 м/с²]

1.26. Радиус-вектор материальной точки изменяется со временем по закону 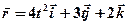. Запишите зависимости скорости и ускорения от времени. Определите модуль скорости в момент времени 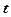= 2 с. [16,3 м/с]

1.27. Диск радиусом 10 см вращается вокруг не­подвижной оси так, что зависимость угла поворота ради­уса диска от времени задается уравнением 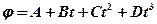( 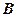= 1 рад/с, 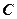= 1 рад/с², 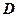= 1 рад/с³). Определите для точек на ободе диска к концу второй се­кунды после начала движения тангенциальное, нормальное и полное ускоре­ния. [1,4 м/с²; 28,9 м/с²; 28,9 м/с²]

1.28. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 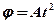( 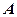=0,5 рад/с²). Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное, нормальное и полное ускорения. [1) 2 рад/с; 2) 1 рад/с²; 3) 0,8 м/с², 3,2 м/с², 3,3 м/с²]

1.29. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 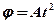( 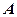=0,1рад/с²). Определите полное ускорение точки на ободе диска к концу второй секунды после начала движения, если в этот момент линейная скорость этой точки 0,4 м/с. [0,25 м/с²]

1.30. Диск радиусом 0,2 м вращается вокруг неподвижной оси так, что зависимость угловой скорос­ти от времени задается уравнением 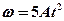, где 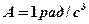. Определите для точек на ободе диска к концу первой секунды после начала движения полное ускорение и число оборотов, сделанных диском за первую минуту движения. [5,8 м/c²; 15, 9]

1.31. Диск радиусом 10 см вращается так, что зависимость угла поворота радиуса диска от времени задается уравнением 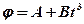( 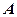= 2 рад, 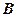= 4 рад/с³). Определите для точек на ободе колеса: 1) нормальное ус­корение в момент времени 2 с; 2) тангенциальное ускорение для этого же момента; 3) угол поворота, при котором полное ускорение составляет с радиусом колеса 45°. [1) 230 м/с²; 2) 4,8 м/с²; 3) 2,67 рад]

1.32. Якорь электродвигателя, имеющий частоту вращения 50 с^-1, после выключения тока, сделав 628 оборотов, остановился. Определите угловое ускорение якоря. [12,5 рад/с²]

1.33. Колесо автомобиля вращается равнозамедленно. За время 2 мин оно изменило частоту вращения от 240 до 60 мин^-1. Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время. [1) 0,157 рад/с²; 2) 300]

1.34. Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найдите угловое ускорение колеса. [3,2 рад/с²]

1.35. Колесо спустя 1 мин после начала вращения приобретает скорость, соответствующую частоте 720 об/мин. Найдите угловое ускорение колеса и число оборотов, сделанных колесом за эту минуту. Движение считать равноускоренным. [1,26 рад/с²; 360 об]

1.36. Колесо, вращаясь равнозамедленно, при торможении уменьшило частоту вращения за 1 мин с 300 об/мин до 180 об/мин. Найдите угловое ускорение колеса и число оборотов, сделанных за это время. [ 0,21 рад/с²; 240 об]

Основные законы и формулы

• Импульс материальной точ­ки

,

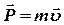где 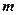-масса материальной точки, 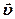- скорость движения.

• Второй закон Ньютона (основное уравнение динами­ки материальной точки)

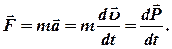
· Это же уравнение в проекциях на касательную и нор­маль к траектории движения точки

,

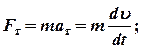
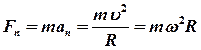где 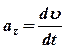- тангенциальное (касательное) ускорение,

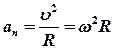- нормальное(центростремительное) ускорение.

• Сила трения скольжения

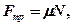
где 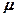— коэффициент трения скольжения; 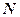— сила нормального давления.

• Сила упругости

,

где 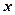- величина деформации; 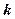- коэффициент жесткости.

· Сила гравитационного притяжения двух материальных точек

,

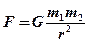где 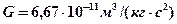– гравитационная постоянная, 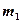и 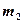– массы взаимодействующих точек, 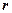- расстояние между точками.

• Закон сохранения импульса для замкнутой систе­мы

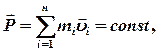
где 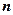- число материальных точек (или тел), входящих в систему.

• Общая скорость тел после неупругогосоударения

,

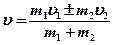где 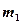и 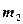- массы тел, 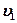и 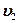- их скорости до взаимодействия.

• Скорости тел после упругогосоударения

; .

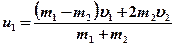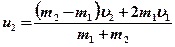• Работа, совершаемая телом

,

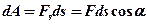где 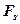— проекция силы на направление перемещения; 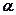— угол между направлениями силы и перемещения.

• Работа, совершаемая переменной силой, на пути

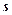
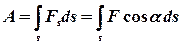
• Средняя мощность за промежуток времени

,

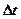
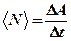где 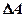– работа за промежуток времени .

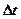• Мгновенная мощность

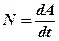, или .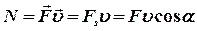

• Кинетическая энергия движущегося со скоростью 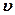тела массой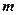

.

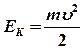· Потенциальная энергия тела массой 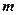, поднятого над поверхностью земли на высоту ,

,

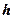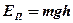где 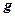- ускорение свободного падения.

• Потенциальная энергия упругодеформированного тела

.

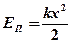• Потенциальная энергия гравитационного взаимодействия

.

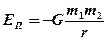· Закон сохранения механической энергии (для консервативной системы)

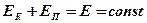
Задания

2.1. Тело массой 2 кг движется прямолинейно по закону 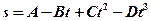( 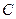= 2 м/с², 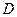= 0,4 м/с³). Определите силу, действую­щую на тело в конце первой секунды движения. [3,2 Н]

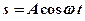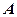2.2. Тело массой m движется так, что зависимость пройденного пути от времени описывается уравнением , где и 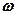— постоянные. Запишите закон изменения силы от времени. [ ]

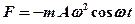2.3. Под действием постоянной силы 9,8 Н тело движется прямолинейно так, что зависимость пройденного пути от времени даётся уравнением 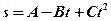, где 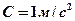. Найдите массу тела. [4,9 кг]

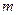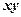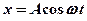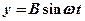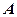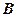2.4. Тело массой движется в плоскости по за­конам , , где , и 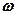— некоторые постоянные. Определите модуль силы, действующей на это тело. [ ]

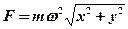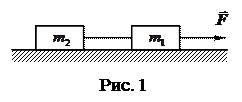2.5. Два груза ( 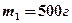и 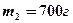) связаны невесомой нитью и лежат на гладкой гори­зонтальной поверхности (рис. 1). К грузу 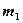приложена гори­зонтально направленная сила 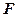= 6Н. Пренебрегая тре­нием, определите: 1) ускорение грузов; 2) силу натяже­ния нити . [1) 5 м/с²; 2) 3,5Н]

2.6. Два груза одинаковой массы ( 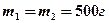) связаны невесомой нитью и лежат на гори­зонтальной поверхности (рис. 1). К одному грузу приложена гори­зонтально направленная сила = 5 Н. Коэффициент тре­ния каждого груза о поверхность равен 0,1. Определите: 1) ускорение грузов; 2) силу натяже­ния нити . [1) 4 м/с²; 2) 2 Н]

2.7. Тело массой 2 кг падает вертикально с ус­корением 5 м/с². Определите силу сопротивления тела о воздух. [10 Н]

2.8. К нити подвешен груз массой 500 г. Опре­делите силу натяжения нити, если нить с грузом под­нимать с ускорением 2м/с². [6 Н]

2.9. К нити подвешен груз массой 500 г. Опре­делите силу натяжения нити, если нить с грузом опускать с ускорением 2м/с². [4 Н]

2.10. На шнуре, перекинутом через неподвижный блок, подвешены грузы массами 0,3 и 0,2 кг. С каким ускорением движутся грузы? Какова сила натяжения шнура во время движения? [2м/с²; 2,4 Н]

2.11. На нити, перекинутой через неподвижный блок, подвешены грузы массами 0,3 и 0,34 кг. За 2 с после начала движения каждый груз прошёл путь 1,2 м. По данным опыта найдите ускорение свободного падения. [9,6 м/с²]

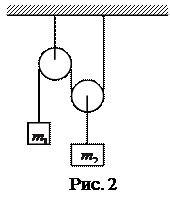
2.12. На рис. 2 изображена система блоков, к которым подвешены грузы массами 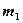= 200 г и 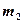= 500 г. Счи­тая, что груз 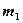поднимается, а подвижный блок с грузом 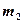опускается, нить и блоки невесомы, силы трения от­сутствуют, определите: 1)силу натяжения нити; 2) ус­корения, с которыми движутся грузы.

[1) 2,3 Н; 2) 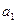= 1,54 м/с², 3) 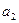= 0,77 м/с²]

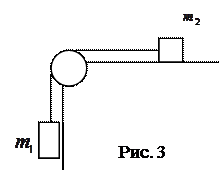
2.13. Под действием груза массой 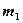=100 г (рис. 3) брусок массой 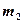=400 г проходит из состояния покоя путь 80 см за 2 с. Найдите коэффициент трения. [0,2]

2.14. Грузы одинаковой массой ( 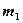= = 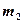0,5 кг) со­единены нитью и перекинуты через невесомый блок, ук­репленный на конце стола (рис. 3). Коэффициент тре­ния груза 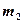о стол 0,15. Пренебрегая трением в бло­ке, определите: 1) ускорение, с которым движутся грузы; 2) силу натяжения нити.

[1) 4,25 м/с²; 2 ) 2,875 Н].

2.15. Система грузов (рис. 3) массами 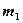= 0,6 кг и 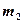= 0,5 кг находится в лифте, движущемся вверх с ускорением 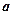=5 м/с². Определите силу натяжения нити, если коэффициент трения между грузом массы 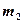и опорой 0,1. [4,5 Н]

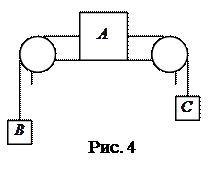2.16. Тело 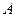массой 2 кг (рис. 4) находится на го­ризонтальном столе и соединено нитями посредством бло­ков с телами 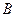( 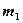= 0,5 кг) и 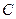( 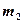= 0,3 кг). Считая нити и блоки невесомыми и пренебрегая силами трения, опре­делите: 1) ускорение, с которым будут двигаться эти тела; 2) разность сил натяжения нитей. [1) 0,7 м/с²; 2) 1,4 Н]

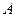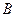2.17. С каким ускорением движется система, изображённая на рис. 4, если масса тел и равна 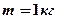, а масса тел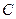а равна 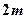. Коэффициент трения равен 0,2. Определите силы натяжения нити, связывающей тела 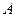и 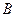, и силы натяжения нити, связывающей тела 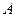и 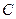. [2,7 м/с²; 12,7 Н; 14,6 Н]

2.18. По наклонной плоскости с углом наклона к горизонту, равным 30°, скользит тело. Определите ско­рость тела в конце второй секунды от начала скольже­ния, если коэффициент трения 0,15. [7,4 м/с]

2.19. С вершины клина, длина которого 2 м и вы­сота 1 м, начинает скользить небольшое тело. Коэф­фициент трения между телом и клином 0,15. Опре­делите ускорение, с которым движется тело, время прохождения тела вдоль клина и скорость тела у осно­вания клина.[3,7 м/с²; 1,04 с; 3,85 м/с]

2.20. На наклонной плоскости длиной 5 м и высотой 3 м находится груз массой 50 кг. Какую силу, направленную вдоль плоскости, надо приложить, чтобы тянуть груз вверх с ускорением 1 м/с²? Коэффициент трения 0,2. [430 Н]

2.21. На наклонной плоскости длиной 5 м и высотой 3 м находится груз массой 50 кг. Какую силу, направленную вдоль плоскости, надо приложить, чтобы удержать этот груз? Коэффициент трения 0,2. [220 Н]

2.22. Вагон массой 1 т спускается по канатной железной дороге с уклоном 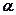= 15° к горизонту (рис. 5). Принимая коэффициент трения 0,05, определите си­лу натяжения каната при торможении вагона в конце спуска, если скорость вагона перед торможением 2,5 м/с, а время торможения 6с. [2,48 кН]

2.23. В установке (рис. 6) угол 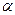наклонной плоскости с го­ризонтом равен 30°, массы тел 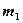=200 г и 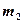=300 г. При этом тело массой 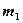движется вверх по наклонной плоскости. Коэффициент трения 0,1. Считая нить и блок невесомыми опреде­лите ускорение, с которым будут двигаться эти тела и силу натяжения нити. [2,29 м/с² ; 1,9 Н]

2.24. В установке (рис. 6) угол 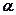наклонной плоскости с го­ризонтом равен 30°, массы тел 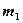=500 г и 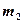=200 г. При этом тело массой 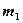движется вниз по наклонной плоскости. Коэффициент трения 0,1. Считая нить и блок невесомыми опреде­лите ускорение, с которым будут двигаться эти тела и силу натяжения нити. [0,15 м/с² ; 2,03 Н]

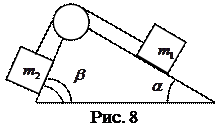
2.25. На тело (рис. 7) массой 10 кг, лежащее на наклонной плоскости ( 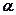= 30°), действует горизон­тально направленная сила 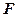= 8 Н. Коэффициент трени­я 0,1. Определите ускорение тела. [4,9 м/с²]

2.26. В установке (рис. 8) углы 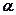и 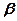с горизонтом со­ответственно равны 30° и 45°, массы тел 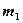=0,45 кг и 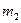=0,5 кг. Считая нить и блок невесомыми и пренебре­гая силами трения, определите: 1) ускорение, с которым движутся тела; 2) силу натяжения нити. [1) 1,35 м/с²; 2) 2,86 Н]

2.27. В установке (рис. 8) углы 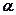и 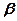с горизонтом со­ответственно равны 30° и 45°, массы тел 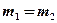= 1 кг. Коэффициент трения каждого тела о плоскость равен 0,1. Считая нить и блок невесомыми определите: 1) ускорение, с которым движутся тела; 2) силу натяжения нити. [1) 0,25 м/с²; 2) 6,1 Н]

2.28. К потолку вагона, движущегося в горизонтальном направлении с ускорением 10 м/с², подвешен на нити шарик массой 200 г. Определите для установившегося движения: 1) силу натяжения нити; 2) угол отклонения нити от вертикали. [1) 2,8 Н; 2) 45°]

2.29. Камень, привязанный к верёвке длиной 50 см, вращается в вертикальной плоскости. Найти, при каком числе оборотов в секунду верёвка оборвётся, если известно, что она разрывается при нагрузке, равной десятикратному весу камня. [2,1 об/с]

2.30. Камень, привязанный к верёвке, вращается в вертикальной плоскости. Найти массу камня, если известно, что разность между максимальным и минимальным натяжениями верёвки равна 10 Н. [0,5 кг]

2.31. Гирька, привязанная к нити длиной 30 см, описывает в горизонтальной плоскости окружность радиусом 15 см. Найдите частоту вращения гирьки. [59 об/мин]

2.32. Диск вращается вокруг вертикальной оси с частотой 30 об/мин. На расстоянии 20 см от оси вращения на диске лежит тело. Каков должен быть коэффициент трения между диском и телом, чтобы тело не скатилось с диска? [0,2]

2.33. С какой скоростью должен ехать автомобиль массой 2 т по выпуклому мосту с радиусом кривизны 40 м, чтобы в верхней точке он перестал оказывать давление на мост? [72 км/ч]

2.34. Шар массой 10 кг сталкивается с шаром массой 4 кг. Скорость первого шара 4 м/с, второго 12 м/с. Найти общую скорость шаров после удара в двух случаях: когда малый шар нагоняет большой шар, движущийся в том же направлении, и когда шары движутся навстречу друг другу. Удар считать прямым, центральным, неупругим. [6,29 м/с; 0,57 м/с]

2.35. Шар массой 200 г, движущийся со скоростью 10 м/с, ударяет неподвижный шар массой 800 г. Удар прямой, центральный, абсолютно упругий. Определите проекции скоростей шаров после удара. (Направление оси выбрать по движению первого шара до удара). [- 6 м/с; 4 м/с]

2.36. Граната, летящая со скоростью 10 м/с разорвалась на два осколка. Больший осколок, масса которого составляет 60% массы всей гранаты, продолжал двигаться в том же направлении, но с увеличенной скоростью, равной 25 м/с. Найдите скорость меньшего осколка. [-12,5 м/с]

2.37. Человек, стоящий в лодке, сделал шесть шагов вдоль лодки и остановился. На сколько шагов передвинулась лодка, если: 1) масса лодки в два раза больше массы человека; 2) масса лодки в два раза меньше массы человека? [2 шага; 4 шага]

2.38. В лодке массой 240 кг стоит человек массой 60 кг. Лодка плывет со скоростью 2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью 4м/с относительно лодки. Найти скорость лодки после прыжка человека: а) вперед по движению лодки; б) в сторону, противоположную движению лодки. [1м/с; 3 м/с]

2.39. Тележка, масса которой (без человека) 120 кг, движется по инерции по горизонтальной плоскости со скоростью 6 м/с. С тележки соскакивает человек массой 80 кг под углом 30^° к направлению ее движения. Скорость тележки уменьшается при этом до 4 м/с. Какова была скорость прыжка относительно плоскости? [10,4 м/с]

2.40. Шарик массой 10 г падает на горизонтальную плоскость с высоты 27 см. Найти среднюю силу удара в следующих случаях: а) шарик пласти­линовый (абсолютно неупругий удар); б) шарик и плоскость из стали (абсолютно упругий удар); в) шарик пластмассовый и после удара подни­мается на высоту 12 см. Длительность удара шарика с плоскостью 0,03 с. [0,77 Н; 1,53 Н; 1,28 Н]

2.41. Движущееся тело массой 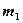ударяется о неподвижное тело массой 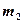. Считая удар неупругим и центральным, найдите, какая часть первоначальной кинетической энергии переходит при ударе в тепло. [ ]

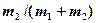2.42. Груз массой 1 кг, висящий на нити, отклоняют на угол 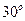. Найдите натяжение нити в момент прохождения грузом положения равновесия. [12,7 Н]

2.43. Груз массой 80 кг поднимают вдоль наклонной плоскости с ускорением 1 м/с². Длина наклонной плоскости 3 м, угол ее наклона к горизонту равен 30°, а коэффициент трения 0,15. Определите работу, совер­шаемую подъемным устройством, его среднюю и максимальную мощности. Началь<