Тема 3. Криволинейный интеграл первого рода.
Тема 1. Двойной интеграл.
Задача 1.Вычислить двойной интеграл от функции 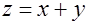 по области, представляющей собой треугольник с вершинами в точках
по области, представляющей собой треугольник с вершинами в точках 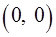 ,
, 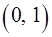 и
и 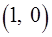 .
.
Задача 2.Расставить пределы интегрирования в повторном интеграле от функции 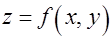 по области, ограниченной линиями
по области, ограниченной линиями 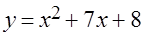 и
и 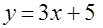 .
.
Задача 3.Изменить порядок интегрирования в повторном интеграле
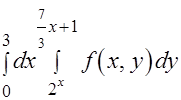 .
.
Задача 4.Изменить порядок интегрирования в повторном интеграле
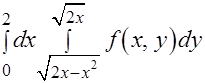 .
.
Задача 5.Изменить порядок интегрирования в повторном интеграле
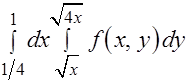 .
.
Задача 6.Вычислить двойной интеграл от функции 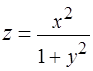 по области
по области 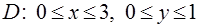 .
.
Задача 7. Вычислить двойной интеграл от функции 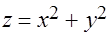 по области, ограниченной линиями
по области, ограниченной линиями 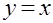 ,
, 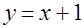 ,
, 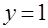 и
и 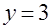 . (Указание: перейти к повторному интегралу, принимая в качестве внешней переменной
. (Указание: перейти к повторному интегралу, принимая в качестве внешней переменной 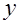 .)
.)
Задача 8.Вычислить двойной интеграл от функции 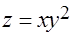 по области, заданной неравенствами
по области, заданной неравенствами 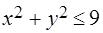 ,
, 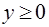 . (Указание: перейти к полярным координатам.)
. (Указание: перейти к полярным координатам.)
Задача 9.Используя переход к полярным координатам, вычислить двойной интеграл 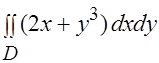 , где
, где 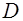 — часть кругового сектора единичного радиуса с центром в начале координат, расположенная в 1-м квадранте.
— часть кругового сектора единичного радиуса с центром в начале координат, расположенная в 1-м квадранте.
Задача 10. Используя переход к полярным координатам, вычислить двойной интеграл от функции 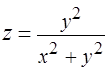 по области, ограниченной линией
по области, ограниченной линией 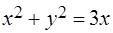 .
.
Задача 11. Найти площадь плоской области, ограниченной линиями 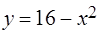 ,
, 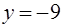 .
.
Задача 12. Найти площадь плоской области, ограниченной линиями 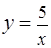 ,
, 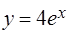 ,
, 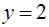 ,
, 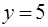 .
.
Задача 13. Найти массу пластинки плотности 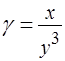 , заданной неравенствами
, заданной неравенствами 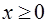 ,
, 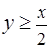 ,
, 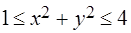 .
.
Задача 14. Найти объем тела, ограниченного поверхностями 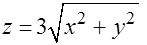 ,
, 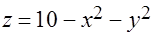 .
.
Задача 15. Найти объем цилиндроида, ограниченного поверхностью 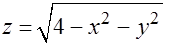 , цилиндром
, цилиндром 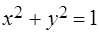 и частью координатной плоскости
и частью координатной плоскости 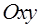 .
.
Задача 16. Найти объем тела, ограниченного поверхностями 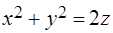 ,
, 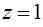 ,
, 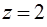
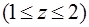 .
.
Задача 17. Найти координаты центра тяжести однородной пластинки, ограниченной линиями 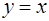 ,
, 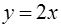 ,
, 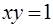 .
.
Тема 2. Тройной интеграл.
Задача 1.Вычислить 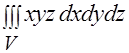 , где
, где 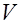 — треугольная пирамида с вершинами в точках
— треугольная пирамида с вершинами в точках 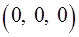 ,
, 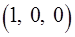 ,
, 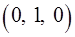 и
и 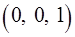 .
.
Задача 2.Расставить пределы интегрирования в повторном (тройном) интеграле от функции 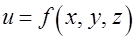 по области
по области 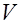 , ограниченной поверхностями
, ограниченной поверхностями 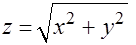 и
и 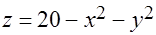 .
.
Задача 3.Вычислить тройной интеграл от функции 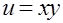 по области, ограниченной поверхностями
по области, ограниченной поверхностями 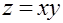 ,
, 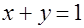 и
и 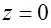
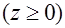 .
.
Задача 4.Используя переход к цилиндрическим координатам, вычислить тройной интеграл от функции 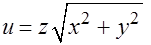 по области, ограниченной поверхностями
по области, ограниченной поверхностями 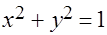 ,
, 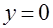 ,
, 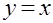 ,
, 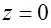 ,
, 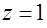 .
.
Задача 5.Вычислить тройной интеграл от функции 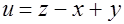 по области, ограниченной поверхностями
по области, ограниченной поверхностями 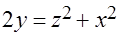 и
и 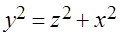 . (Указание: выбрать в качестве внешних переменных
. (Указание: выбрать в качестве внешних переменных 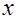 и
и 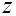 и перейти к цилиндрическим координатам.)
и перейти к цилиндрическим координатам.)
Задача 6.Вычислить интеграл 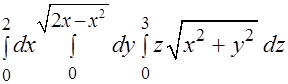
с помощью перехода к цилиндрическим координатам.
Задача 7.Вычислить интеграл
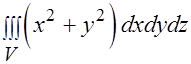
по области, заданной неравенствами 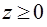 ,
, 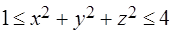 . (Указание: перейти к сферическим координатам.)
. (Указание: перейти к сферическим координатам.)
Задача 8.Вычислить с помощью тройного интеграла объем тела 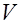 , ограниченного поверхностями
, ограниченного поверхностями 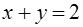 ,
, 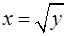 ,
, 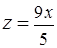 ,
, 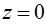 .
.
Задача 9.Вычислить с помощью тройного интеграла объем тела 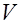 , ограниченного поверхностями
, ограниченного поверхностями 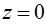 ,
, 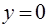 ,
, 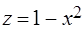 ,
, 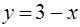 .
.
Задача 10.Найти центр тяжести однородного полушара 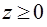 ,
, 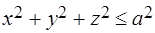 .
.
Тема 1. Двойной интеграл.
Задача 1.Вычислить двойной интеграл от функции 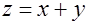 по области, представляющей собой треугольник с вершинами в точках
по области, представляющей собой треугольник с вершинами в точках 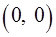 ,
, 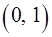 и
и 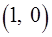 .
.
Задача 2.Расставить пределы интегрирования в повторном интеграле от функции 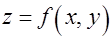 по области, ограниченной линиями
по области, ограниченной линиями 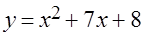 и
и 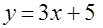 .
.
Задача 3.Изменить порядок интегрирования в повторном интеграле
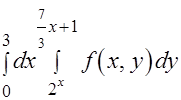 .
.
Задача 4.Изменить порядок интегрирования в повторном интеграле
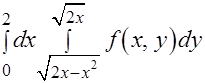 .
.
Задача 5.Изменить порядок интегрирования в повторном интеграле
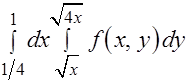 .
.
Задача 6.Вычислить двойной интеграл от функции 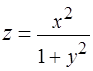 по области
по области 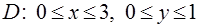 .
.
Задача 7. Вычислить двойной интеграл от функции 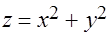 по области, ограниченной линиями
по области, ограниченной линиями 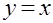 ,
, 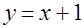 ,
, 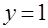 и
и 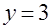 . (Указание: перейти к повторному интегралу, принимая в качестве внешней переменной
. (Указание: перейти к повторному интегралу, принимая в качестве внешней переменной 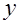 .)
.)
Задача 8.Вычислить двойной интеграл от функции 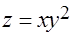 по области, заданной неравенствами
по области, заданной неравенствами 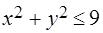 ,
, 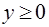 . (Указание: перейти к полярным координатам.)
. (Указание: перейти к полярным координатам.)
Задача 9.Используя переход к полярным координатам, вычислить двойной интеграл 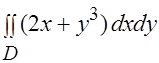 , где
, где 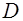 — часть кругового сектора единичного радиуса с центром в начале координат, расположенная в 1-м квадранте.
— часть кругового сектора единичного радиуса с центром в начале координат, расположенная в 1-м квадранте.
Задача 10. Используя переход к полярным координатам, вычислить двойной интеграл от функции 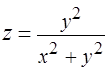 по области, ограниченной линией
по области, ограниченной линией 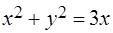 .
.
Задача 11. Найти площадь плоской области, ограниченной линиями 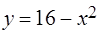 ,
, 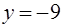 .
.
Задача 12. Найти площадь плоской области, ограниченной линиями 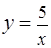 ,
, 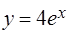 ,
, 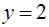 ,
, 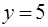 .
.
Задача 13. Найти массу пластинки плотности 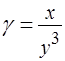 , заданной неравенствами
, заданной неравенствами 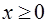 ,
, 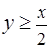 ,
, 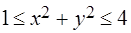 .
.
Задача 14. Найти объем тела, ограниченного поверхностями 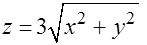 ,
, 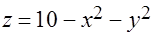 .
.
Задача 15. Найти объем цилиндроида, ограниченного поверхностью 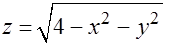 , цилиндром
, цилиндром 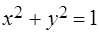 и частью координатной плоскости
и частью координатной плоскости 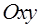 .
.
Задача 16. Найти объем тела, ограниченного поверхностями 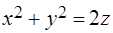 ,
, 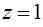 ,
, 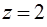
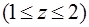 .
.
Задача 17. Найти координаты центра тяжести однородной пластинки, ограниченной линиями 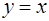 ,
, 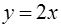 ,
, 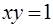 .
.
Тема 2. Тройной интеграл.
Задача 1.Вычислить 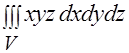 , где
, где 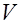 — треугольная пирамида с вершинами в точках
— треугольная пирамида с вершинами в точках 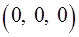 ,
, 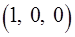 ,
, 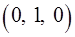 и
и 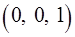 .
.
Задача 2.Расставить пределы интегрирования в повторном (тройном) интеграле от функции 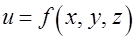 по области
по области 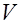 , ограниченной поверхностями
, ограниченной поверхностями 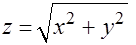 и
и 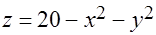 .
.
Задача 3.Вычислить тройной интеграл от функции 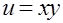 по области, ограниченной поверхностями
по области, ограниченной поверхностями 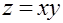 ,
, 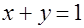 и
и 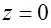
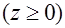 .
.
Задача 4.Используя переход к цилиндрическим координатам, вычислить тройной интеграл от функции 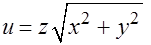 по области, ограниченной поверхностями
по области, ограниченной поверхностями 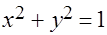 ,
, 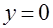 ,
, 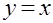 ,
, 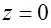 ,
, 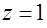 .
.
Задача 5.Вычислить тройной интеграл от функции 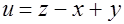 по области, ограниченной поверхностями
по области, ограниченной поверхностями 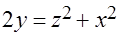 и
и 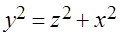 . (Указание: выбрать в качестве внешних переменных
. (Указание: выбрать в качестве внешних переменных 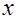 и
и 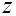 и перейти к цилиндрическим координатам.)
и перейти к цилиндрическим координатам.)
Задача 6.Вычислить интеграл 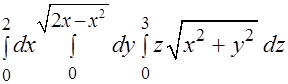
с помощью перехода к цилиндрическим координатам.
Задача 7.Вычислить интеграл
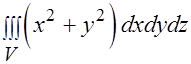
по области, заданной неравенствами 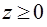 ,
, 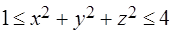 . (Указание: перейти к сферическим координатам.)
. (Указание: перейти к сферическим координатам.)
Задача 8.Вычислить с помощью тройного интеграла объем тела 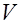 , ограниченного поверхностями
, ограниченного поверхностями 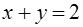 ,
, 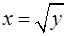 ,
, 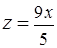 ,
, 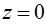 .
.
Задача 9.Вычислить с помощью тройного интеграла объем тела 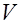 , ограниченного поверхностями
, ограниченного поверхностями 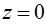 ,
, 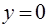 ,
, 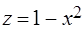 ,
, 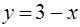 .
.
Задача 10.Найти центр тяжести однородного полушара 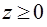 ,
, 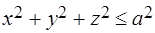 .
.
Тема 3. Криволинейный интеграл первого рода.
Задача 1.Вычислить криволинейный интеграл 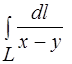 , где
, где 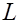 — отрезок прямой
— отрезок прямой 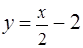 , заключенный между точками
, заключенный между точками 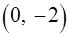 и
и 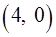 .
.
Задача 2.Вычислить криволинейный интеграл 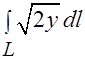 , где
, где 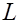 — первая арка циклоиды
— первая арка циклоиды 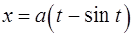 ,
, 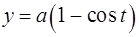 .
.
Задача 3.Вычислить криволинейный интеграл 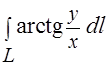 , где
, где 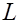 — часть спирали Архимеда
— часть спирали Архимеда 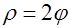 , заключенная внутри круга радиуса
, заключенная внутри круга радиуса 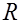 с центром в начале координат.
с центром в начале координат.
Задача 4.Найти массу четверти эллипса, расположенной в первом квадранте, если плотность в каждой точке равна ординате этой точки.
Задача 5.Найти массу кривой с линейной плотностью 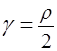 , заданной в полярных координатах уравнением
, заданной в полярных координатах уравнением 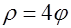 , где
, где 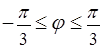 .
.
Задача 6.Найти массу кривой с линейной плотностью  , заданной в полярных координатах уравнением
, заданной в полярных координатах уравнением 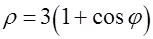 , где
, где 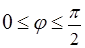 .
.
Задача 7.Найти массу кривой с линейной плотностью 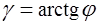 , заданной в полярных координатах уравнением
, заданной в полярных координатах уравнением 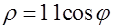 , где
, где 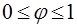 .
.
Задача 8.Вычислить длину линии 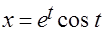 ,
, 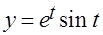 ,
, 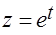 от точки
от точки 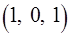 до точки
до точки 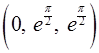 .
.
Задача 9.Найти центр тяжести и моменты инерции первого витка однородной винтовой линии 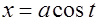 ,
, 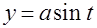 ,
, 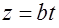 .
.
