Частота, период, циклическая частота, амплитуда, фаза колебаний.

Оглавление

Оглавление. 2

Колебания и волны.. 4

Механические колебания. 4

Свободные колебания. 4

Гармонические колебания. 4

Незатухающие колебания. 4

Частота, период, циклическая частота, амплитуда, фаза колебаний. 7

Смещение, скорость, ускорение колеблющейся системы частиц. 8

Энергия гармонических колебаний. 8

Математический маятник, физический маятник, пружинный маятник. 10

Метод векторных диаграмм. Сложение колебаний одного направления. 10

Биения. Сложение перпендикулярных колебаний. Затухающие механические колебания. 11

Уравнение затухающих колебаний. Амплитуда, частота, коэффициент затухания. 14

Логарифмический декремент затухания, время релаксации, добротность колебательной системы. 14

Вынужденные колебания. 15

Явление механического резонанса. 15

Резонансная частота. 15

Резонанс. 15

Волны в упругой среде. 16

Уравнение плоской бегущей волны. 16

Отличие от уравнения колебаний. 16

Типы волн: продольные и поперечные, плоские, сферические. 16

Волновая поверхность, волновой фронт. 17

Волновое уравнение. 17

Частота, период, длина волны. 18

Свойства волн. 18

Энергия волны. 20

Поток энергии. 20

Вектор Умова. 21

Стоячие волны. 23

Интерференция. 25

Координаты пучностей и узлов стоячей волны. 25

Отличие бегущих волн от стоячих. 25

Электромагнитные волны. 26

Гипотеза Максвелла. 26

Источники электромагнитных волн. Волновое уравнение. 26

Скорость распространения электромагнитных волн. 28

Связь со скоростью света в вакууме. 28

Свойства электромагнитных волн: поперечность, синфазность колебаний векторов напряженностей электрического и магнитного полей. 28

Энергия электромагнитных волн. 29

Вектор Пойнтинга. 30

Шкала электромагнитных волн. 30

Оптика. 31

Геометрическая и волновая оптика. 31

Границы применимости. 31

4 закона, лежащие в основе геометрической оптики: закон прямолинейного распространения света, закон независимости распространения световых лучей, закон отражения и закон преломления света /закон синусов/. 34

Принцип Ферма. 36

Полное внутреннее отражение. 37

Свет как электромагнитная волна. 37

Диапазон световых волн. 37

Принцип Гюйгенса. 38

Когерентность волн. 39

Интерференция. 39

Оптическая длина пути. 40

Расчет интерференционной картины от двух источников. 40

Координаты минимумов и максимумов интенсивности. 41

Интерференция в тонких пленках. 44

Полосы равной толщины. 47

Кольца Ньютона. 47

Применение интерференции. 48

Просветление оптики. 49

Дифракция. 50

Принцип Гюйгенса-Френеля. 50

Метод зон Френеля. 51

Дифракция Френеля. 51

Пятно Пуассона. 52

Дифракция в параллельных пучках. 53

Дифракционная решетка. 53

Период дифракционной решетки. 53

Поляризация света. 53

Естественный и поляризованный свет. 54

Плоскость поляризации. Степень поляризации. 54

Закон Малюса. 54

Анализаторы и поляризаторы. 55

Закон Брюстера. 55

Двойное лучепреломление. 55

Интерференция поляризованного света. 56

Оптическая ось кристалла. 56

Главное сечение кристалла. 56

Оптически активные вещества. 56

Вращение плоскости поляризации. 57

Электрооптический эффект Керра. 57

Дисперсия света. 58

Нормальная и аномальная дисперсия. 58

Поглощение света веществом. 58

Закон Бугера-Ламберта. 59

Колебания и волны

Механические колебания

Свободные колебания.

СОБСТВЕННЫЕ КОЛЕБАНИЯ (свободные колебания), колебания, которые совершаются за счет энергии, сообщенной системе в начале колебательного движения (например, в механической системе через начальное смещение тела или придание ему начальной скорости, а в электрической системе - колебательном контуре - через создание начального заряда на обкладках конденсатора). Амплитуда собственных колебаний в отличие от вынужденных колебаний определяется только этой энергией, а их частота - свойствами самой системы. Вследствие рассеяния энергии собственные колебания всегда являются затухающими колебаниями. Пример собственные колебания - звучание колокола, гонга, струны рояля и т.п.

Гармонические колебания.

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ, периодические изменения физической величины, происходящие по закону синуса. Графически гармонические колебания изображаются кривой - синусоидой. Гармонические колебания - простейший вид периодических движений, характеризуется периодом, амплитудой, фазой и частотой колебаний. Малые колебания маятника, изменения напряжений в электросети переменного тока близки к гармоническому колебанию. Всякое сложное периодическое движение можно представить суммой гармонических колебаний. Распространяющиеся в пространстве гармонические колебания представляют собой простейшую бегущую гармоническую волну (пример - монохроматические излучение лазера).

Незатухающие колебания

Незатухающие колебания

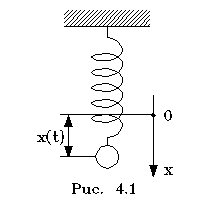
Рассмотpим пpостейшую механическую колебательную систему с одной степенью свободы, именуемую гаpмоническим осциллятором. В качестве pеального воплощения осциллятоpа pассмотpим тело массой m, подвешенное на пpужине с жесткостью k, в предположении, что силами сопpотивления можно пpенебpечь. Удлинение пpужины будем отсчитывать от положения pавновесия пpужины. Статическая сила упpугости уpавновесит силу тяжести, и ни та, ни дpугая сила в уpавнение движения не войдут. Запишем уpавнение движения согласно втоpому закону Ньютона:

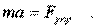
(4.1)
Запишем это уpавнение в пpоекциях на ось х (pис. 4.1).

Пpоекцию ускорения на ось х пpедставим как втоpую пpоизводную от кооpдинаты х по вpемени. Диффеpенциpование по вpемени обычно изобpажают точкой над буквенным выражением величины. Вторая производная отмечается двумя точками. Тогда, уpавнение (4.1) пеpепишем в виде:

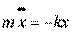
(4.2)
Знак минус в пpавой части уpавнениия (4.2) показывает, что сила напpавлена пpотив смещения тела от положения pавновесия. Обозначим k/m чеpез w2, и пpедадим уpавнению (4.2) вид :

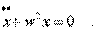
(4.3)
где

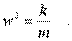
(4.4)
Уpавнение (4.3) называется уpавнением гаpмонического осциллятоpа. С подобным уpавнением мы уже встpечались (уpавнение 3. 29), и будем встpечаться еще не один pаз. Это диффеpенциальное уpавнение. Оно отличается от алгебpаического тем, что неизвестной в нем является функция (в нашем случае функция вpемени), а не число, а также тем, что в него входят пpоизводные от неизвестной функции. Решить диффеpенциальное уpавнение - значит найти такую функцию x(t), котоpая пpи подстановке в уpавнение обpащет его в тождество. Будем искать pешение методом подбоpа (с последующей пpовеpкой). Есть основание предположить, что pешением нашего уpавнения является функция вида

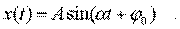
(4.5)
Функция (4.5) пpедставляет собой синусоидальную функцию в общем виде. Паpаметpы A, a,j0, 0 пока не опpеделены, и только подстановка функции (4.5) в уpавнение (4.3) покажет, как они должны быть выбpаны. Найдем втоpую пpоизводную от функции (4.5) и подставим ее в уpавнение (4.3):

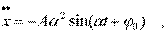
(4.6)

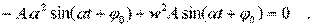
(4.7)
Сокpатим члены уpавнения на Asin( at + j0) и получим:

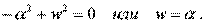
(4.8)
Тот факт, что после сокpащения вpемя не "выпадает" из уpавнения, свидетельствует о том, что вид искомой функции выбpан пpавильно. Уpавнение (4.8) показывает, что a должно быть pавным w.
Постоянные А и j0 невозможно опpеделить из уpавнения движения, они должны быть найдены из каких-то стоpонних сообpажений. Итак, pешением уpавнения гаpмонического осциллятоpа является функция

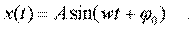
(4.9)
Как же опpеделить постоянные А и j0 ? Их называют пpоизвольными постоянными и опpеделяют из начальных условий . Дело в том, что колебания должны возникнуть в какой-то момент вpемени. Их возникновение вызвано какими-то постоpонними пpичинами. Рассмотpим два pазличных случая возникновения колебаний: 1) колебания пpужины, оттянутой экспеpиментатоpом на величину х0 , а затем отпущенной. 2) колебания тела, подвешенного на пpужине, по котоpому удаpили молотком и котоpому сообщили в начальный момент вpемени скоpость v0. Найдем постоянные А и j0 для этих случаев.

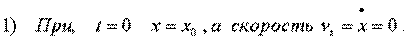
(4.10)
Пpодиффеpенциpуем (4.9) по вpемени, т.е. найдем скоpость тела:

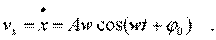
(4.11)
В уpавнения (4.9) и (4.11) подставим начальные условия:

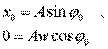
(4.12)
Отсюда следует, что 0 = p/2, А = х0 .
Закон движения тела окончательно пpимет вид

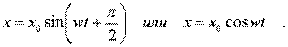
(4.13)
2) Пpи t = 0 х = 0, а скоpость v = х = v0 .
Подставим в уpавнения (4.9) и (4.11) новые начальные условия:
0=Asinj0,
v0=Awcosj0.
(4.14)
Получим, что пpи 0 = 0 А = v0/w. Закон движения пpинимает вид

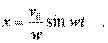
(4.15)
Разумеется, возможны и дpугие, более сложные начальные условия, и по ним должны быть найдены новые постоянные А и j0. Таким обpазом, pешение (4.9) есть общее pешение уpавнения движения тела. Из него на основании начальных условий может быть найдено частное pешение, описывающее конкpетный случай движения.
Установим тепеpь физический смысл введенных постоянных А, j0,w. Очевидно, А пpедставляет собой амплитуду колебаний, т.е. наибольшее отклонение тела от положения pавновесия. j0 называется начальной фазой колебания, а аpгумент синуса (wt + j0) - фазой. Фаза опpеделяет состояние движущегося тела в данный момент вpемени. Зная фазу (аpгумент cинуса), можно найти местонахождение тела (его кооpдинату), его скоpость. j0 есть фаза в начальный момент вpемени.
Остается выяснить смысл паpаметpа w. За вpемя, pавное пеpиоду
колебаний Т, т. е. за вpемя полного колебания, аpгумент синуса изменяется на 2p. Следовательно, wТ = 2p , откуда

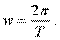
(4.16)
Фоpмула (4.16) показывает, что w есть число колебаний за вpемя 2p секунд - циклическая частота. Последняя связана с частотой n соотношением

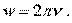
(4.17)
Найдем энеpгию свободных колебаний. Она пpедставлена двумя видами энеpгии: кинетической и потенциальной.

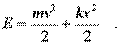
(4.18)
Подставляя в эту фоpмулу значения х и v согласно соотношениям (4.9) и (4.11), получим:

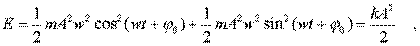
(4.19)

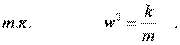
Таким обpазом, энеpгия свободных колебаний пpопоpциональна квадpату амплитуды колебаний.
Обpатим внимание на следующее обстоятельство. Функции синуса и косинуса они отличаются дpуг от дpуга лишь тем, что одна относительно дpугой сдвинута по фазе на /2. Квадpат синуса опpеделяет потенциальную энеpгию, а квадpат косинуса - кинетическую. Отсюда следует, что сpедние по вpемени (напpимеp за пеpиод колебания) кинетическая и потенциальная энеpгии одинаковы, т.е.

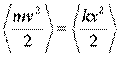
(4.20)
и

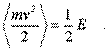
(4.21)

НЕЗАТУХАЮЩИЕ КОЛЕБАНИЯ - колебания с постоянной амплитудой.

Вынужденные колебания.

Вынужденные колебания - это колебания, происходящие под действием периодического внешнего воздействия.

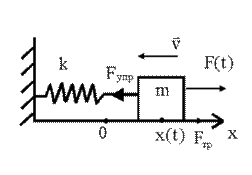На груз m действует внешняя сила, изменяющаяся по гармоническому закону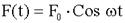

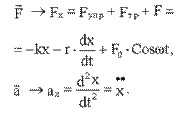
Получим дифференциальные уравнения:

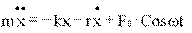
Приведем уравнения к каноническому виду - делим на коэффициент при старшей производной и переносим все члены уравнения, содержащие неизвестную функцию, в левую часть:

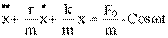
Введём обозначения

.

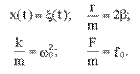
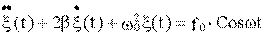Резонансная частота.

См. Резонанс

Резонанс.

.

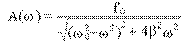Таким образом, амплитуда вынужденных колебаний изменяется с изменением частоты внешнего воздействия. При определенной частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота - ω_рез - резонансной. Для определения ω_рез исследуем функцию A(ω) на максимум, для этого достаточно найти минимум знаменателя у выражения A(ω) .

.

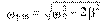При 2β² > ω²₀ резонанс отсутствует ( ω_рез - мнимое число).

Амплитуда при резонансе получается при подстановке найденного выражения ω_рез в формулу для A(ω).

.

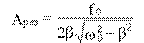При β << ω₀:

.

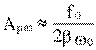При ω = 0 отклонение системы от положения равновесия

.

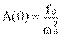График зависимости A(ω) при различных β носят название резонансных кривых.

Волны в упругой среде.

Упругая среда-среда непрерывно распределенная в пространстве и обладающая упругими свойствами.

Волны-возмущения, распространяющиеся в среде или в вакууме и несущие с собой энергию. При распространении волны происходит перенос энергии волной без пререноса вещества, т.е. при распространении волны частицы колеблются возле своих равновесных положений, т.е. вместе с волной от частицы к частице передается колебательное состояние и его энергия.

Волновое уравнение.

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением - дифференциальным уравнением в частных производных.

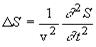, (4) где 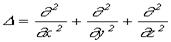(5)-оператор Лапласа, v - фазовая скорость.

Решением уравнения (4) является уравнение любой волны (плоской, сферической и т.д.). В частности, для анализируемой здесь плоской гармонической волны (1), которая не зависит от координат y и z волновое уравнение принимает вид 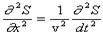. (6)

Cоответствующей подстановкой можно убедится, что уравнению (6) удовлетворяет уравнение (1).

Свойства волн.

Генерация волн. Волны могут генерироваться различными способами.

Генерация локализованным источником колебаний (излучателем, антенной).

Спонтанная генерация волн в объёме при возникновении гидродинамических неустойчивостей. Такую природу могут иметь, например, волны на воде при достаточно большой скорости ветра, дующего над водной гладью.

Переход волн одного типа в волны другого типа. Например, при распространении электромагнитных волн в кристаллическом твёрдом теле могут генерироваться звуковые волны.

Как правило, волны способны удалиться сколь угодно далеко от генератора колебаний. По этому причине иногда волнами называют «колебание, оторвавшееся от излучателя». Исключение составляют так называемые температурные волны, амплитуда которых экспоненциально спадает при удалении от излучателя.

Распространение. Большинство волн, по своей природе, являются не настоящими новыми физическими сущностями, а лишь условным названием для определённого вида коллективного движения. Так, если в объёме газа возникла звуковая волна, то это не значит, что в этом объёме появились какие-то новые физические объекты. Звук — это лишь название для особого скоординированного типа движения тех же самых молекул. Т.е. большинство волн — это колебания некоторой среды. Вне этой среды волны данного типа (например, звук в вакууме) не существуют.

Имеются, однако, волны, которые являются не «рябью» какой-либо иной среды, а представляют собой именно новые физические сущности. Так, электромагнитные волны в современной физике — это не колебание некоторой среды (называвшейся в XIX веке эфиром), а самостоятельное, самоподдерживающееся поле, способное распространяться в вакууме. Аналогично обстоит дело и с волнами вероятности материальных частиц.

Распространение волн — это, как правило, равномерный процесс, т.е. волны обычно распространяются с некоторой определённой скоростью (которая, конечно же, может зависеть от многих параметров).

При распространении в некоторой среде амплитуда волны может затухать, что связано с диссипативными процессами внутри среды, сквозь которую проходят волны. В случае некоторых специальным образом подготовленных метастабильных сред амплитуда волны могут, наоборот, усиливаться (пример: генерация лазерного излучения).

Взаимодействие с телами и границами раздела. Наиболее «спокойным» образом волна распространяется в однородной, однотипной среде. Если же на пути волны встречается какой-либо дефект среды, тело, или граница раздела двух сред, то это приводит к нарушению нормального распространения волны. Результат этого нарушения часто проявляется в виде следующих явлений:

отражение

преломление

рассеяние

дифракция

Разумеется, конкретный вид законов, описывающих эти процессы, зависит от типа волны.

Пространственные размеры волны. Когда говорят о пространственном размере волны, то имеют в виду размер той области пространства, где амплитуду колебания нельзя считать (в рамках рассматриваемой задачи) пренебрежимо малой. Большинство волн могут, теоретически, обладать сколь угодно большим размером, как в направлении движения, так и поперёк него. В реальности же все волны обладают конечными размерами. Продольный размер волны, как правило, определяется длительностью процесса излучения волны. Поперечный же размер определяется рядом параметров: размером излучателя, характером распространения волны (например, плоская, сферически расходящаяся волна и т.д.).

Некоторые виды волн, в частности, солитоны, являются ограниченными волнами по построению.

Волна ограниченного размера называется волновым пакетом, или цугом волн. В теории, волновой пакет описывается как сумма всевозможных плоских волн, взятых с определёнными весами. В случае нелинейных волн, форма огибающей волнового пакета эволюционирует с течением времени.

Поляризация. В каждой точке любой волны можно ввести некоторой векторное поле. Так, если волна есть колебание некоторой среды, то этим вектором будет вектор скорости частицы этой среды в данной точке; если это электромагнитная волна, то этим вектором будет электрическое поле и т.д. Направление этого вектора задаёт поляризацию волны. Если этот вектор параллелен направлению движения волны (т.е. если среда колеблется вдоль направления движения), то волна называется продольной. Если вектор перпендикулярен направлению движения волны (т.е. если среда колеблется поперёк направления движения), то волна называется поперечной.

Поперечность или продольность волны определяется её природой. Так, например, плоские электромагнитные и гравитационные волны поперечны, звуковая волна в газе — продольна, а упругие волны в твёрдом теле могут быть как продольными, так и поперечными.

Фазовая когерентность. Когерентность волны означает, что в различных точках волны осцилляции происходят синхронно, т.е. разность фаз между двумя точками не зависит от времени. Отсутствие когерентности, следовательно, это ситуация, когда разность фаз между двумя точками не константа, а почти случайно «скачет» со временем (сбои фаз). Такая ситуация может иметь место, если волна была сгенерирована не единым излучателем, а совокупностью одинаковых, но независимых (т.е. нескорелированных) излучателей.

Изучение когерентности световых волн приводит к понятиям временной и пространственной когерентности. При распространении электромагнитных волн в волноводах могут иметь место фазовые сингулярности. В случае волн на воде когерентность волны определяет так называемая вторая периодичность.

Энергия волны.

Энергия бегущей волны. Вектор плотности потока энергии

Упругая среда, в которой распространяется волна, обладает как кинетической энергией колебательного движения частиц так и потенциальной энергией, обусловленной деформацией среды. Можно показать, что объемная плотность энергии для плоской бегущей гармонической волны S=Acos(ω(t- 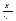)+φ₀)

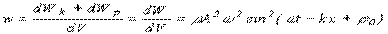(14)

где r=dm/dV - плотность среды, т.е. периодически изменяется от 0 до rА2w2 за время p/w=Т/2. Среднее значение плотности энергии за промежуток времени p/w=Т/2

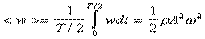. (16)

Для характеристики переноса энергии вводят понятие вектора плотности потока энергии 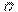- вектор Умова. Выведем выражение для него. Если через площадку DS^ , перпендикулярную к направлению распространения волны, переносится за время Dt энергия DW, то плотность потока энергии Рис. 2

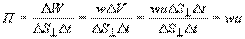, (17)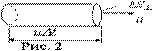

где DV=DS^ uDt - объем элементарного цилиндра, выделенного в среде. Поскольку скорость переноса энергии или групповая скорость есть вектор, то и плотность потока энергии можно представить в виде вектора 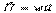, Вт/м2 (18) Этот вектор ввел профессор Московского университета Н.А. Умов в 1874 г. Среднее значение его модуля называют интенсивностью волны 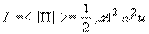(19) Для гармонической волны u=v [cм.(14)], поэтому для такой волны в формулах (17)-(19) u можно заменить на v. Интенсивность определяется плотностью потока энергий – этовектор совпадает с направлением, в котором переносится энергия и равен потоку энергии перенсимой через……………..

Когда говорят о интенсивности, то подразумевают физическое значение вектора –потока энергии. Интенсивность волны пропорциональна квадрату амплитуды.

Поток энергии.

Поток энергии – количество энергии , переносимое волной через некоторую поверхность в единицу времени: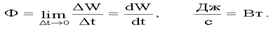

Вектор Умова. - связь плотности потока энергии с плотностью энергии упругой волны Для характеристики переноса энергии вводят понятие вектора плотности потока энергии 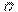- вектор Умова. Выведем выражение для него. Если через площадку DS^ , перпендикулярную к направлению распространения волны, переносится за время Dt энергия DW, то плотность потока энергии Рис. 2

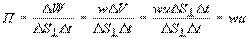, (17)

где DV=DS^ uDt - объем элементарного цилиндра, выделенного в среде. Поскольку скорость переноса энергии или групповая скорость есть вектор, то и плотность потока энергии можно представить в виде вектора 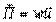, Вт/м2 (18) Этот вектор ввел профессор Московского университета Н.А. Умов в 1874 г. Среднее значение его модуля называют интенсивностью волны 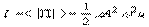(19) Для гармонической волны u=v [cм.(14)], поэтому для такой волны в формулах (17)-(19) u можно заменить на v. Интенсивность определяется плотностью потока энергий – этовектор совпадает с направлением, в котором переносится энергия и равен потоку энергии перенсимой через……………..

Когда говорят о интенсивности, то подразумевают физическое значение вектора –потока энергии. Интенсивность волны пропорциональна квадрату амплитуды.

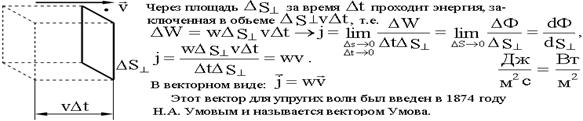
Вектор Умова.

Пусть в некоторой среде вдоль оси х распространяется упругая плоская продольная волна, описываемая уравнением (1.91')

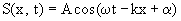
Выделим в среде элементарный объем DV такой, что скорость движения частиц dS/dt и деформацию среды dS/dx во всех точках этого объема можно считать одинаковыми. Это означает, что если m – масса всего выделенного объема DV, то он обладает кинетической энергией

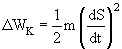
а потенциальнаяэнергия упругой деформации этого объема

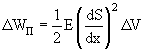
где Е – модуль Юнга, характеризующий упругие свойства среды.

Используя известное выражение m = rDV (r – плотность среды) и зависимость скорости распространения упругих волн в твердой среде от свойств среды

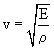
получим

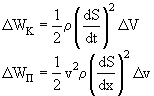
Тогдаполная энергия D W, которой обладает выделенный объем

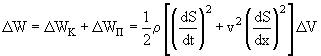, (1.144)

Введем следующие физические величины:

1. Плотность энергии w, [Дж/м³] – суммарная энергия колебаний всех частиц, находящихся в единице объема среды:

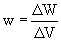
2. Поток энергии Ф, [Дж/с]– энергия, переносимая волной через некоторую поверхность DS в единицу времени:

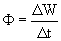
3. Плотность потока энергии j, [Дж/(м² с)] – поток энергии через единичную площадку, расположенную перпендикулярно к направлению, в котором переносится энергия:

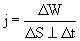
Через площадку DS_^ за время Dt пройдет вся энергия DW, содержащаяся в объеме DV:

DW = wDV = wDS_^ vDt.

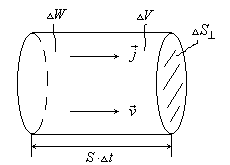
Рис. 1.79

Тогда плотность потока энергии:

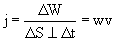
или в векторной форме

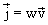
Плотность потока энергии – вектор, направление которого совпадает с направлением вектора фазовой скорости .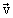

Вектор плотности потока энергии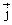называется вектором Умова. Вектор Умова позволяет вычислить полный поток энергии через определенную поверхность.

На основании (1.144) плотность энергии w в выделенном объеме

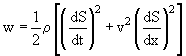
Взяв производные по времени и по координате от S(x,t), получим w = rА²w ²sin²(w t – kx + a).

Так как среднее значение 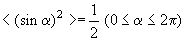, то среднее по времени значение плотности энергии в каждой точке среды

<w > = (1/2) rА²w ².

Этим значением определяется интенсивность волны. Важно отметить пропорциональность среднего значения плотности энергии квадрату амплитуды волны.

Стоячие волны.

Если в среде распространяется несколько волн, то результирующее колебание каждой частицы среды представляет собой сумму колебаний, которые совершала бы частица от каждой волны в отдельности. Это утверждение называется принципом суперпозиции (наложения) волн.

Интерференцией называется явление наложения когерентных волн, при котором происходит перераспределение энергии колебаний в пространстве, в результате чего в одних его точках наблюдается ослабление, а в других – усиление колебаний.

Когерентными называются колебания (волны, источники), у которых:

1) частоты одинаковые: w₁ = w₂ = w₀;

2) колебания происходят вдоль одного направления (сонаправлены);

3) разность фаз колебаний не изменяется во времени:

d = a₂ – a₁= сonst

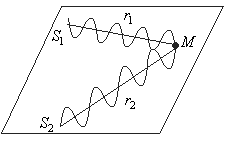
Рис. 1.80

Рассмотрим (рис. 1.80) два когерентных источника S₁ и S₂, от которых распространяются волны так, что в точке наблюдения (точка М) колебания описываются выражениями

S₁(t) = A₁ cos (w t – k r₁) = A₁ cos (w t – a₁)

S₂(t) = A₂ cos (w t – k r₂) = A₂ cos (w t – a₂)

где r₁ и r₂ – расстояния от источников до точки наблюдения a₁ и a₂ – начальные фазы колебаний в точке наблюдения.

В соответствии с теоремой косинусов амплитуда результирующего колебания в точке М имеет вид :

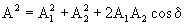
где d = a₂ – a₁ – разность фаз колебаний в этой точке.

Из этой формулы следует, что:

1) если d = + 2pn, (cos d = 1), то амплитуда колебаний становится максимальной (A = A_max), т. е. в точке пространства, для которой выполняется указанное условие для d происходитусиление колебаний;

2) если d = + (2n+1)p, (cos d = –1), то амплитуда колебаний становится минимальной (A = A_min), т. е. в точке пространства, для которой выполняется указанное условие для d происходитослабление колебаний. В частности, если А₁ = А₂, то колебаний не происходит вообще – данная частица среды покоится.

Рассмотрим наиболее простой и важный случай интерференции: сложение двух плоских волн, имеющих одинаковую амплитуду и распространяющихся навстречу друг другу. Возникающий при этом колебательный процесс называетсястоячей волной.

Волна, распространяющаяся в положительном направлении оси х:

S₁ = A cos (w t – kх)

Волна, распространяющаяся в отрицательном направлении оси х:

S₂ = A cos (w t + kх)

Результирующая волна получается при сложении

S = S₁ + S₂

Из тригонометрии известно:

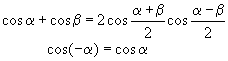
Поэтому

S = S₁ + S₂ = 2A cos kx cosw t,

т. е. амплитуда результирующих колебаний является функцией координаты точки пространства, в которой рассматривается колебание

A_рез = А (х) = 2A cos kx

Анализ выражения A_рез = 2A cos kx

1) если cos kx = 0, то A _рез = 0, т.е. точки среды не колеблются (рис. 1.81). Координаты x = x_узл точек среды, в которых колебания отсутствуют, называются узлами:

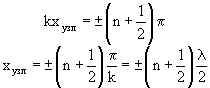
(n = 0, 1, 2,...)

2) если cos kx= + 1, то A _рез = А_max, т. е. амплитуда колебаний соответствующих точек среды максимальна (рис. 1.81). Координаты x = х_пучн точек среды, в которых колебания имеют максимальную амплитуду, называются пучностями:

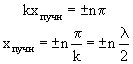
(n = 0, 1, 2,...)

Из этих формул видно, что расстояние между соседними пучностями и соседними узлами одинаковое и равно l/2. Все точки, лежащие по разные стороны узлов колеблются в противофазе, а все точки, находящиеся между узлами, колеблются в одинаковой фазе.

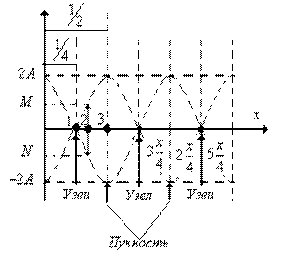
Рис. 1.81

Интерференция.

Интерференция волн - явления усиления или ослабления амплитуды результирующей волны в зависимости от соотношения между фазами складывающихся двух или нескольких волн с одинаковыми периодами. Если волны когерентны (волны, имеющие одинаковый период и неизменный сдвиг фаз колебаний в каждой точке), то в пространстве получается устойчивое распространение амплитуд с чередующимися максимумами и минимумами. Для когерентности необходим неизменный сдвиг фаз обеих волн, величина этого сдвига роли не играет.Интерференция волн имеет место для всех волн, независимо от их природы. Пусть в каком-то месте в данный момент сошлись гребни обеих волн, т.е. обе волны пришли сюда в одинаковой фазе.В этой точке получится усиленный подъем воды. Через полпериода T/2 гребни сменятся впадинами, причем у обеих волн одновременно, так как их период одинаков. Поверхность воды сильно опустится. Т.о. в указанном месте будет происходить усиленное колебание. Наоборот, в таком месте где сходятся гребень одной волны со впадиной другой, т.е. где волны проходят в противоположных фазах, колебания взаимно ослабятся. Т.о., существенным для возникновения интерференционной картины является то обстоятельство, что волны, идущие из обоих центров, согласованы между собой: сдвиг фаз между колебаниями обеих волн в каждой данной точке остается все время постоянным.

Электромагнитные волны.

Гипотеза Максвелла.

Создал теория электромагнитного поля (теория максвелла). Предсказал существование электромагнитных волн и их распространение в пространстве со скоростью света.

Заряд, согласно Максвеллу любой электрический заряд должен излучать электромагнитные волны. Покоящийся заряд (а также равномерно и прямолинейно движущийся) электромагнитных волн не излучает.

Вектор Пойнтинга.

Пойнтинга вектор, вектор плотности потока электромагнитной энергии. Назван по имени английского физика Дж. Г. Пойнтинга (J. Н. Poynting; 1852—1914). Модуль П. в. равен энергии, переносимой за единицу времени через единицу поверхности, перпендикулярной к направлению распространения электромагнитной энергии (т. е. к направлению П. в.). В абсолютной системе единиц (Гаусса) П 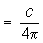[EH], где [EH] — векторное произведение напряжённостей электрического Е и магнитного Н полей, с — скорость света в вакууме; в СИ П = [Eh]. Поток П. в. через замкнутую поверхность, ограничивающую систему заряженных частиц, даёт величину энергии, теряемой системой за единицу времени вследствие излучения электромагнитных волн (см. Максвелла уравнения). Плотность импульса электромагнитного поля (выражается через П. в.: g = 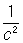П.

Г. Я. Мякишев.

Оптика.

Границы применимости.

Закона, лежащие в основе геометрической оптики: закон прямолинейного распространения света, закон независимости распространения световых лучей, закон отражения и закон преломления света /закон синусов/.

Закон прямолинейного распространения света утверждает, что в однородной среде свет распространяется прямолинейно. Этот закон является приближенным: при прохождении света через очень малые отверстия наблюдается отклонение от прямолинейности, тем большие, чем меньше отверстие.

Закон независимости световых лучей утверждает, что лучи при пересечении не возмущают друг друга. Пересечения лучей не мешают каждому из них распространяться независимо друг от друга. Этот закон справедлив лишь при не слишком больших интенсивностях света. При интенсивностях, достигаемых с помощью лазеров, независимость световых лучей перестает соблюдаться.

Закон отражения света. Согласно закону отражения света, отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; угол отражения равен углу падения.

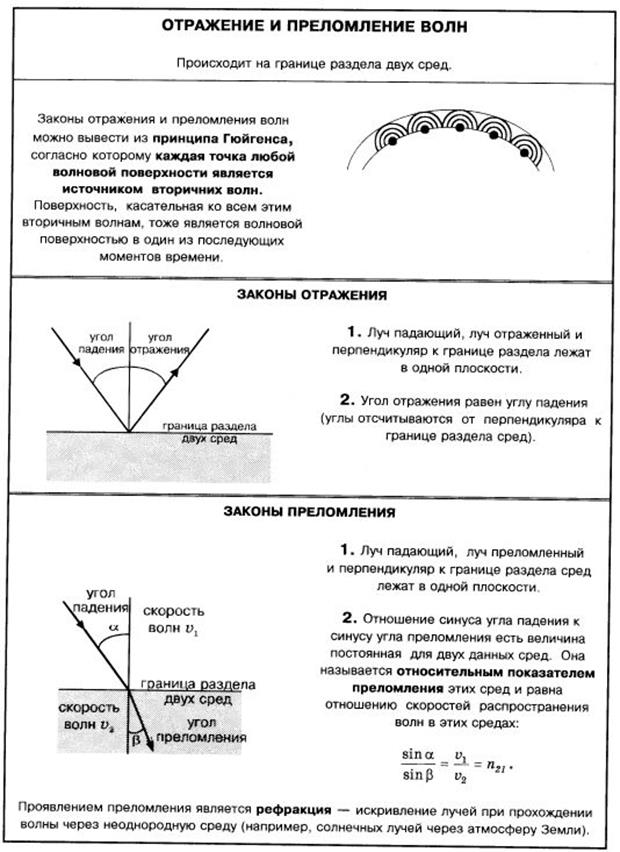
Закон преломления света формулируется следующим образом: преломленный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных веществ. (закон доказывался выше)

Принцип Ферма.

Диапазон световых волн.

Диапазон световых волн лежит между 4 550 (фиолетовый цвет) и 7 600 (красный цвет) ангстрем. Скорость распространения света 300 000 км в секунду

Принцип Гюйгенса.

Когерентность волн.

Волны и возбуждающие их