Определение отношения теплоёмкостей воздуха в процессах при постоянном давлении и при постоянном объёме методом Клемана и Дезорма

Выполнил:

студент группы РТбо1-11

Черняков Е.Д.

9 октября 2015 г.

Преподаватель: Арзуманян Г. В.

Таганрог 2015 г.

Цель работы.

Изучение термодинамических процессов в газе и экспериментальное определение показателя адиабаты воздуха методом Клемана и Дезорма.

Приборы и принадлежности.

Стеклянный баллон, U-образный водяной манометр, ручной насос (компрессор).

Краткие теоретические сведения.

Идеальный газ — математическая модель газа, в которой в рамках молекулярно-кинетической теории предполагается, что: 1) потенциальной энергией взаимодействия частиц, составляющих газ, можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объём частиц газа пренебрежимо мал; 3) между частицами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги; 4) время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями. В расширенной модели идеального газа частицы, из которого он состоит, имеют форму упругих сфер или эллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц. В рамках термодинамики идеальными называются гипотетические (реально не существующие) газы, подчиняющиеся термическому уравнению состояния Клапейрона — Менделеева.

Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точного уравнения состояния реальных газов, например, уравнения Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.

Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана) и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми — Дирака или Бозе — Эйнштейна).

Уравнение состояния — уравнение, связывающее между собой термодинамические (макроскопические) параметры системы, такие, как температура, давление, объём, химический потенциал и др. Уравнение состояния можно написать всегда, когда можно применять термодинамическое описание явлений. При этом реальные уравнения состояний реальных веществ могут быть крайне сложными.

Уравнение состояния системы не содержится в постулатах термодинамики и не может быть выведено из неё. Оно должно быть взято со стороны (из опыта или из модели, созданной в рамках статистической физики). Термодинамика же не рассматривает вопросы внутреннего устройства вещества.

Заметим, что соотношения, задаваемые уравнением состояния, справедливы только для состояний термодинамического равновесия.

Изобарный процесс

Изобарный (или изобармческий) процесс (от др.-греч. ἴσος «равный» и βάρος «тяжесть, вес») — процесс изменения состояния термодинамической системы при постоянном давлении (P=const).

Зависимость объёма газа от температуры при неизменном давлении была экспериментально исследована в 1802 году Жозефом Луи Гей-Люссаком. Закон Гей-Люссака: При постоянном давлении и неизменных значениях массы идеального газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.

Линия, изображающая изобарный процесс на диаграмме, называется изобарой.

Изохорный процесс

Изохорный (или изохорический) процесс (от др.-греч. ἴσος «равный» и χώρος «[занимаемое] место») — процесс изменения состояния термодинамической системы при постоянном объёме (V=const). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре: P/T = const.

Линия, изображающая изохорный процесс на диаграмме, называется изохорой.

Подведённая к газу теплота Q в изохорном процессе расходуется на изменение внутренней энергии U газа. Так, для одноатомного идеального газа

Q = ΔU = ³⁄₂νRT = 3V·ΔP,

где R — универсальная газовая постоянная,

ν — количество молей газа,

T — абсолютная температура в кельвинах,

V — объём газа,

ΔP — приращение давления.

Изотермический процесс

Изотермический процесс (от др.-греч. ἴσος «равный» и θέρμη «жар») — процесс изменения состояния термодинамической системы при постоянной температуре (T=const). Изотермический процесс в идеальных газах описывается законом Бойля — Мариотта:

При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.

Изоэнтропийный процесс

Изоэнтропийный процесс — процесс изменения состояния термодинамической системы при постоянной энтропии (S=const). Изоэнтропийным является, например, обратимый адиабатический процесс: в таком процессе не происходит теплообмена с окружающей средой. Идеальный газ в таком процессе описывается следующим уравнением

Определение отношения теплоёмкостей воздуха в процессах при постоянном давлении и при постоянном объёме методом Клемана и Дезорма - student2.ru

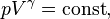
где γ — показатель адиабаты, определяемый типом газа.

Первый закон термодинамики

Первый закон термодинамики — Изменение внутренней энергии ΔU не изолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A внешних сил

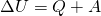
Вместо работы А, совершаемой внешними силами над термодинамической системой, часто удобнее бывает рассматривать работу A’, совершаемую термодинамической системой над внешними телами. Так как эти работы равны по абсолютному значению, но противоположны по знаку:

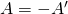
Тогда после такого преобразования первый закон термодинамики будет иметь вид:

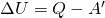
Первый закон термодинамики — В не изолированной термодинамической системе изменение внутренней энергии равно разности между полученным количеством теплоты Q и работой A’, совершаемой данной системой

Говоря простым языком первый закон термодинамики говорит о энергии, которая не может сама создаваться и исчезать в никуда, она передается от одной системы к другой и превращается из одной формы в другую (механическая в тепловую).

Важным следствием первого закона термодинамики является то, что невозможности создать машину (двигатель), которая способна совершать полезную работу без потребления энергии извне. Такая гипотетическая машина получила название вечного двигателя первого рода.

Рис.1

Вычислим работу, которую совершает газ в адиабатическом процессе. Запишем уравнение (1) в виде:
Определение отношения теплоёмкостей воздуха в процессах при постоянном давлении и при постоянном объёме методом Клемана и Дезорма - student2.ru

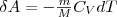
Если газ адиабатически расширяется от объема V₁ до V₂, то его температура уменьшается от T₁ до T₂ и работа расширения идеального газа
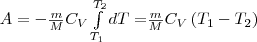Определение отношения теплоёмкостей воздуха в процессах при постоянном давлении и при постоянном объёме методом Клемана и Дезорма - student2.ru (8)

Используя те же приемы, что и при выводе формулы (5), выражение (8) для работы при адиабатическом расширении можно привести к виду
Определение отношения теплоёмкостей воздуха в процессах при постоянном давлении и при постоянном объёме методом Клемана и Дезорма - student2.ru

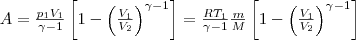
где p₁V₁=(m/M)RT₁

Работа, которую совершает газом при адиабатическом расширении 1—2 (определяется площадью, заштрихованной на рис. 2), меньше, чем при изотермическом, по причине, что при адиабатическом расширении осуществляется охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне такого же количества теплоты.
Рассмотренные изобарный, изохорный, изотермический и адиабатический процессы имеют общую особенность — они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны С_V и С_p, в изотермическом процессе (dT=0) теплоемкость равна ±∞, в адиабатическом (δQ=0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается неизменной, называется политропным.
Исходя из первого начала термодинамики при условии постоянства теплоемкости (C=const) можно вывести уравнение политропы:
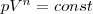Определение отношения теплоёмкостей воздуха в процессах при постоянном давлении и при постоянном объёме методом Клемана и Дезорма - student2.ru (9)

где n=(С—С_p)/(С—С_V)—показатель политропы. Очевидно, что при С=0, n=γ, из (55.9) получается уравнение адиабаты; при С = 0, n = 1 — уравнение изотермы; при С=С_p, n=0 —уравнение изобары, при С=С_V, n=±∞ — уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.

Применение первого начала термодинамики к изопроцессам в идеальном газе. Выясним, какой вид принимает формула Q=AU+A для различных изопроцессов в идеальном газе. Мы уже знаем, что при изохорическом процессе работа газа А равна нулю. Следовательно, формула Q=AU+A для этого процесса принимает вид

Q=AU. (1)

Эго означает, что при изохорическом процессе все подведенное к газу количество теплоты идет на увеличение его внутренней энергии.

Для изобарического процесса формула первого начала термодинамики имеет вид:

Q=AU+A.

Действительно, в этом случае A—p∆V отлично от нуля, так как объем газа непостоянен. Изменение внутренней энергии AU, которое пропорционально приросту температуры, тоже отлично от нуля, поскольку температура газа в этом процессе изменяется. Таким образом, при изобарическом процессе подведенное к газу количество теплоты частично идет на увеличение его внутренней энергии, а частично тратится на выполнение работы газом в процессе его расширения.

При изотермическом процессе температура газа не изменяется. Поэтому можно утверждать, что в этом случае внутренняя энергия газа остается постоянной, т. е. ∆U=0. Следовательно, формула (Q=AU+A) для этого процесса имеет вид

Q=A. (2)

Это означает, что при изотермическом процессе все подведенное к газу количество теплоты идет на выполнение газом работы.

Анализ формулы (Q=AU+A) показывает, что с газом может происходить еще один важный процесс, при котором Q=0. Этот процесс имеет большое практическое значение.

Вывод по работе.