Несобственные интегралы с бесконечными пределами интегрирования.
Определение 5.Пусть функция 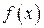 определена на промежутке
определена на промежутке 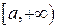 и интегрируема по Риману на любом отрезке
и интегрируема по Риману на любом отрезке 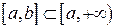 . Если существует (конечный) предел
. Если существует (конечный) предел
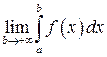 ,
,
то его называют несобственным интегралом (первого рода) и обозначают
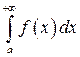 . (31)
. (31)
Таким образом
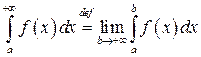 .
.
В этом случае говорят также, что несобственный интеграл (31) сходитсяна промежутке 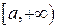 , а функция
, а функция 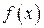 называется интегрируемой (в несобственном смысле) на промежутке
называется интегрируемой (в несобственном смысле) на промежутке 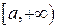 . Если же предел не существует, то говорят, что интеграл расходится.
. Если же предел не существует, то говорят, что интеграл расходится.
Замечания.1)Если 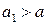 , то интегралы
, то интегралы 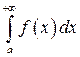 и
и 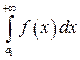 сходятся или расходятся одновременно, т.к.
сходятся или расходятся одновременно, т.к. 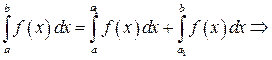
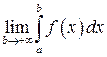 и
и 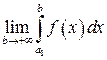 существуют одновременно.
существуют одновременно.
2) Если 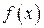 имеет первообразную
имеет первообразную 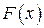 на промежутке
на промежутке 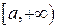 , то
, то
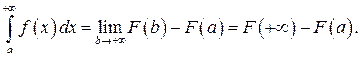
3) Очевидно, что для несобственных интегралов выполняется свойство линейности: если интегралы (31) для 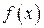 и
и 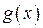 существуют, то
существуют, то
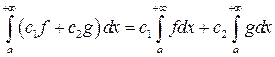
4) Аналогично определяются несобственные интегралы
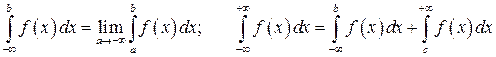 .
.
Поэтому дальше будем рассматривать только интеграл (31).
Примеры. 1) 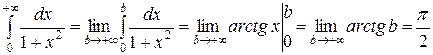 , т. е. данный интеграл сходится.
, т. е. данный интеграл сходится.
2) 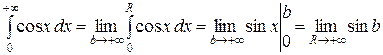 , но предел функции
, но предел функции 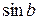 при
при 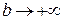 не существует, следовательно, интеграл расходится.
не существует, следовательно, интеграл расходится.
3) 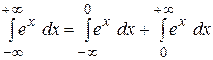 ; интеграл расходится, так как
; интеграл расходится, так как
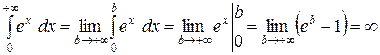 .
.
4) Исследовать сходимость интеграла 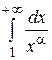 , если
, если 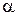 – некоторое число.
– некоторое число.
а) Если α≠1, то для любого 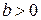
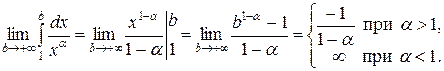
б) Если 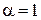 , то для любого
, то для любого 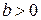
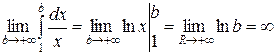 .
.
Таким образом, данный интеграл сходится при 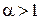 и расходится при
и расходится при 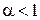 .
.
Теорема 29(критерий Коши).Для того чтобы несобственный интеграл (31) был сходящимся необходимо и достаточно, чтобы выполнялись условия:
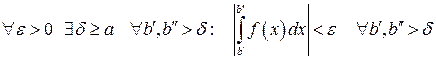 .
.
□ Сходимость интеграла 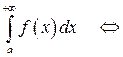 существованию конечного предела
существованию конечного предела 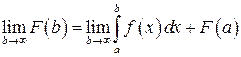 . Но в силу критерия Коши для функции
. Но в силу критерия Коши для функции 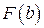 при
при 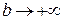 для существования предела необходимо и достаточно, чтобы
для существования предела необходимо и достаточно, чтобы
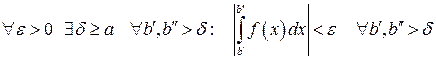
Тогда последнее неравенство можно переписать в виде:
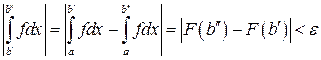 ■ Теорема 30(признак сравнения). Пусть
■ Теорема 30(признак сравнения). Пусть
а) 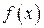 и
и 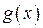 определены на
определены на 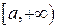 , интегрируемы на
, интегрируемы на 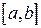 ;
;
б) 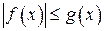 при
при 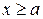 ;
;
в) несобственный интеграл 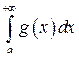 – сходится. Тогда сходится и
– сходится. Тогда сходится и 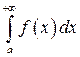 .
.
Поскольку 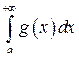 сходится, то по теореме 29 выполняется критерий Коши:
сходится, то по теореме 29 выполняется критерий Коши: 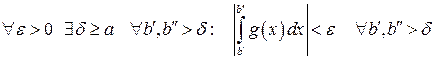 .Теперь проверим критерий Коши для функции
.Теперь проверим критерий Коши для функции 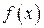 :
: 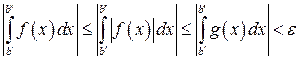 . Критерий Коши выполняется и, следовательно, интеграл сходится. ■
. Критерий Коши выполняется и, следовательно, интеграл сходится. ■
Определение 6. Несобственный интеграл (31) называется абсолютно сходящимся, если сходится интеграл
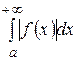 (32)
(32)
Если интеграл (31) сходится, а (32) расходится, то говорят, что интеграл (31) сходится условно. Из теоремы ясно, что если (31) абсолютно сходится, то и просто сходится.
Теорема 31 (основной критерий сходимости).Пусть 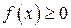 при
при 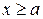 , тогда для сходимости интеграла (31) необходимо и достаточно, чтобы
, тогда для сходимости интеграла (31) необходимо и достаточно, чтобы
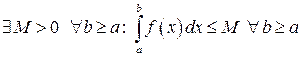 . (33)
. (33)
Функция 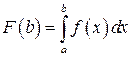 не убывает при
не убывает при 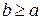 , т.к.
, т.к. 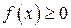 . Поэтому, для сходимости интеграла (31) , т.е. для существования предела, необходимо и достаточно, чтобы функция
. Поэтому, для сходимости интеграла (31) , т.е. для существования предела, необходимо и достаточно, чтобы функция 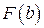 была ограничена сверху:
была ограничена сверху:
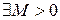 при
при 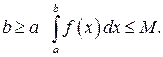 ■
■
Теорема 32 (признак Дирихле).Пусть выполняются следующие условия:
а) функция 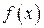 интегрируема по Риману на любом отрезке
интегрируема по Риману на любом отрезке 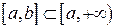
б) 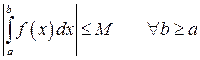 ;
;
в) функция 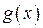 при
при 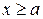 непрерывно дифференцируема и монотонно убывает, стремясь к нулю при
непрерывно дифференцируема и монотонно убывает, стремясь к нулю при 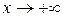 .
.
Тогда 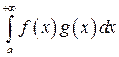 – сходится.
– сходится.
Рассмотрим 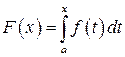 . По условию теоремы функция
. По условию теоремы функция 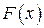 ограничена
ограничена 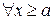 , т.е.
, т.е. 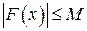 (из условия (а)). Заметим, что
(из условия (а)). Заметим, что 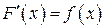 . По формуле интегрирования по частям, имеем:
. По формуле интегрирования по частям, имеем:
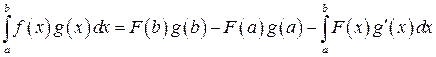 (34)
(34)
Рассмотрим интеграл в правой части и оценим, учитывая, что по условию (в) 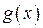 монотонно убывает, следовательно
монотонно убывает, следовательно 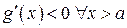 .
.
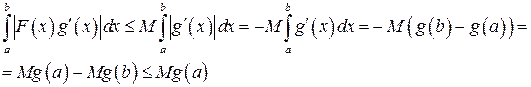
Из теоремы 28 несобственный интеграл  сходится абсолютно, а значит и просто сходится. Следовательно, существует конечный предел
сходится абсолютно, а значит и просто сходится. Следовательно, существует конечный предел 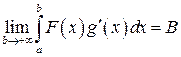 . Т.к.
. Т.к. 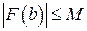 и
и 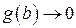 при
при 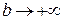 , то
, то 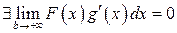 .
.
Следовательно, в правой части (34) существуют пределы всех слагаемых. ■
Примеры. Заметим, что в примерах 1-4 вычисление несобственного интеграла было основано на его определении, однако часто достаточно только исследования сходимости интеграла. Для этого как раз и используются доказанные теоремы.
5)Исследовать сходимость 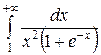 .
.
Решение. Сравним подынтегральную функцию 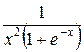 с функцией
с функцией 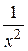 на промежутке
на промежутке 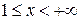 . Очевидно, что
. Очевидно, что
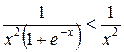 .
.
Но интеграл 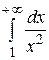 сходится, так как
сходится, так как 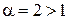 . Следовательно, согласно
. Следовательно, согласно
признаку сравнения сходится и данный интеграл.
6)Исследовать сходимость 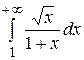 .
.
Решение. Сравнивая подынтегральную функцию 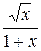 , с функцией
, с функцией 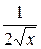 на промежутке
на промежутке 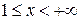 , имеем:
, имеем:
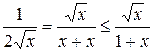 .
.
Но интеграл 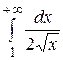 расходится, так как
расходится, так как 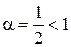 (пример 40). Следовательно, согласно признаку сравнения и данный интеграл расходится.
(пример 40). Следовательно, согласно признаку сравнения и данный интеграл расходится.
7)Интеграл 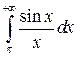 по признаку Дирихле сходится, поскольку:
по признаку Дирихле сходится, поскольку:
а) функция 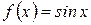 интегрируема на любом отрезке,
интегрируема на любом отрезке,
б) 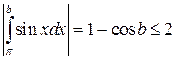 ,
,
в) функция 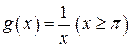 непрерывно дифференцируемая и монотонно убывает при
непрерывно дифференцируемая и монотонно убывает при 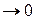 .
.
