Вычисление объема и поверхности тела вращения.

Теорема 27Пусть функция 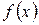непрерывна и неотрицательна на отрезке 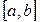. Тогда тело, которое образуется вращением вокруг оси 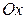криволинейной трапеции, ограниченной сверху графиком функции 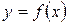, имеет объем

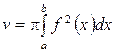. (28)

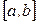□ Рассмотрим разбиение отрезка на 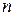частей точками 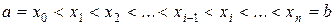. На каждом частичном отрезке 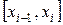возьмем точки 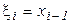и построим прямоугольник MNPQ (рис. 10). При вращении вокруг оси 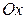каждый прямоугольник опишет цилиндр.

Найдем объем 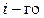цилиндра, образованного вращением прямоугольника :

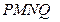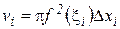, где .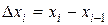

Сумма объемов всех 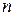цилиндров приближенно равна объему данного тела вращения:

.

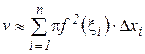С другой стороны, эта сумма является интегральной суммой для интеграла (28). Так как функция 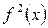непрерывна на 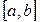, то предел этой суммы при 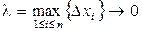существует и равен определенному интегралу (28). Таким образом,

. ■

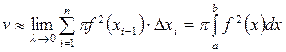Примеры. 1) Найти объем тела, полученного вращением эллипса 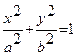вокруг оси Оу.

Решение. .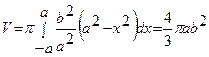

2) Вычислить объем тора. Тором называется тело, получающееся при вращении круга радиуса 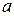вокруг оси, лежащей в его плоскости на расстоянии 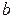от центра круга 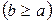. Форму тора имеет, например, баранка.

Решение. Пусть круг вращается вокруг оси 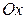(рис. 11). Объем тора можно представить как разность объемов тел, полученных от вращения криволинейных трапеци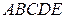й и 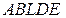вокруг оси .

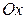Уравнение окружности 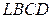имеет вид: ,

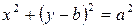причем уравнение кривой

,

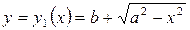а уравнение кривой

,

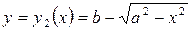Используя формулу (27), получаем для объема тора выражение

.

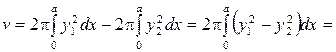
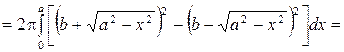
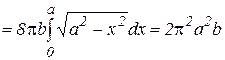Теорема 28 Пусть функция 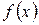неотрицательна и непрерывна вместе со своей первой производной на отрезке 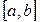. Тогда поверхность, образованная вращением графика этой функции вокруг оси 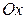, имеет площадь, которая может быть вычислена по формуле

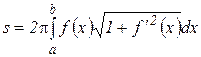. (29)

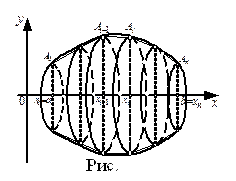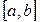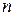□ Разобьем произвольный отрезок на частей точками 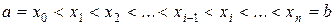.Пусть 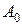, , 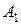,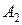…, , 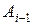,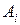…, 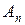– соответствующие точки графика функции 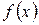. Построим ломанную 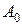, , 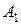,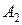…, 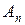(рис. 12). При вращении этой ломанной вокруг оси 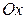получим поверхность, составленную из боковых поверхностей усеченных конусов (цилиндров). Площадь боковой поверхности усеченного конуса (цилиндра), образованного вращением 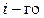звена ломаной, равна 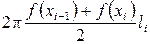– длина хорды 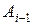, , 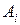т.е.

.

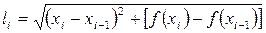По формуле Лагранжа имеем:

.

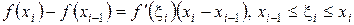Полагая 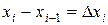, получаем

.

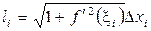Итак, площадь поверхности вращения приближенно равна площади поверхности, полученной от вращения ломанной

.

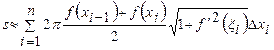Представим эту сумму в виде двух сумм

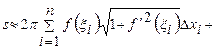
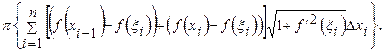
Первая сумма в правой части последнего равенства является интегральной суммой для интеграла (29), и при 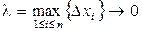в силу непрерывности функции 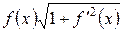имеет своим пределом этот интеграл. Покажем, что выражение в фигурных скобках в правой части равенства имеет при 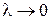предел, равный нулю. Действительно, так как функция 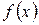равномерно-непрерывна на 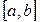, то по теореме Кантора для любого 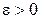существует 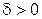такое, что при 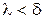выполняются неравенства 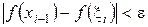и 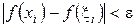. Если обозначить через 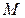максимальное значение функции 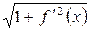на отрезке 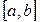, то выражение в фигурных скобках при 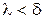оценивается следующим образом:

.

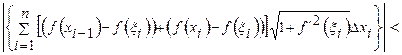
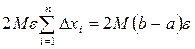Так как 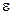произвольно мало, то отсюда следует, что предел указанного выражения равен нулю при .

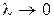Таким образом, переходя в равенстве к пределу при 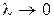, имеем , т.е. получена искомая формула (29). ■

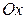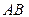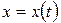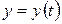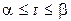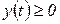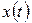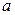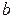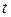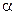Замечание. Если поверхность получена вращением вокруг оси кривой , заданной параметрическими уравнениями , , , причем , а функция изменяется от до при изменении параметра от до 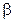, причем 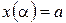, , 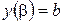то, производя в формуле (29) замену переменной 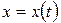, получаем

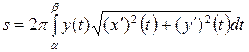. (30)

Наконец, если кривая задана уравнением в полярных координатах: 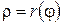, , 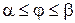где 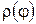имеет непрерывную производную на 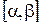, то этот случай сводится к параметрическому заданию кривой 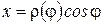, , 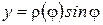, 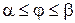и формула (30) принимает вид

.

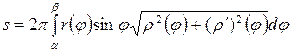Примеры.1) Вычислить площадь поверхности шарового пояса, образованного вращением полуокружности 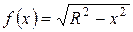, , 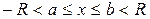вокруг оси .

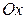Решение. По формуле (29) получаем

,

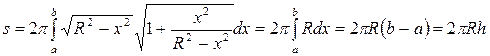где 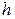– высота пояса.

2) Вычислить площадь поверхности, полученной вращением одной арки циклоиды 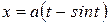, , 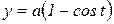, 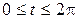вокруг оси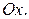

Решение. По формуле (30) имеем

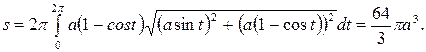
Несобственные интегралы