Площадь поверхности тела вращения

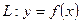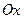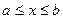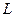Рассмотрим поверхность, образованную вращением кривой вокруг оси (рис. 8.13). Площадь этой поверхности, если и гладкая на 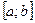кривая определяется выражением

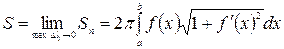(8.15).

Пример 8.7. Найти площадь поверхности сферы, образованной вращением полуокружности 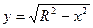вокруг оси 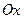(рис.8.16).

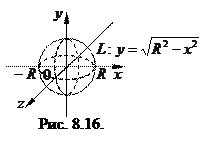Решение. ,

,

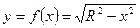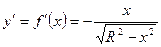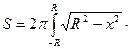
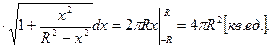
Приложения определенного интеграла в задачах физики и химии.

1. Работа переменной силы. Если переменная сила 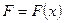действует в направлении оси 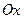, то работа, совершаемая этой силой по перемещению материальной точки на отрезке от 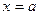до 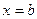, равна .

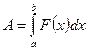2. Путь, пройденный точкой. Если точка перемещается по некоторой траектории с переменной скоростью 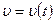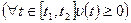, то путь, пройденный точкой за период времени от 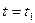до 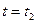, равен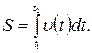

3. Масса прореагировавшего вещества. Если 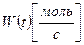– переменная скорость химической реакции (см. п. 1.1), то масса вещества, вступившего в химическую реакцию за промежуток времени от 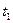до 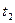, равна .

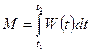4. Масса неоднородного стержня. Если дан тонкий неоднородный стержень с переменной линейной плотностью 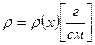, и длина стержня равна 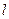, то его масса определяется формулой .

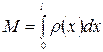Несобственные интегралы.

8.5.1. Несобственные интегралы первого рода (с бесконечными пределами).

Пусть функция 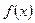определена на промежутке 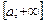и для любого вещественного числа 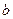, 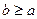существует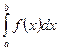

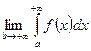называется несобственным интегралом 1 рода от функции 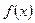на промежутке 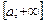и обозначается символом .

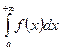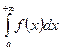
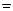
Таким образом, по определению, 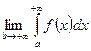(8.16.)

Если предел существует и конечен говорят, что несобственный интеграл (8.16) сходится; если конечного предела не существует, то говорят, что несобственный интеграл (8.16) расходится.

Аналогично определяется несобственный интеграл на промежутке 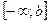: 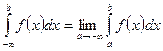(8.17).

Несобственным интегралом от функции 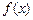на промежутке 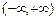называется предел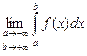

при независимом стремлени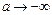и и :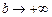

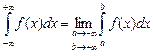(8.18)

Если для некоторого вещественного числа 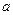сходится каждый из несобственных интегралов 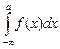и 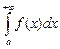, то сходится и неопределенный интеграл 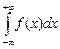, причем .

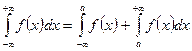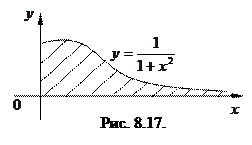Пример 8.8. Вычислить .

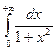Решение. По определению несобственного интервала, имеем

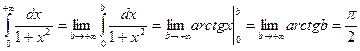, т.е. 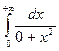сходится. Рассмотренный интеграл выражает площадь заштрихованной области на рис. 8.17.

Пример 8.9. Вычислить .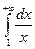

Решение. 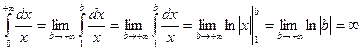, т.е. 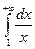расходится.

Во многих случаях бывает достаточно установить, сходится данный интервал или расходуется, и оценить его значение. Сформулируем некоторые достаточные признаки сходимости.

1. Пусть для всех 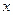, , 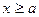выполнено неравенство .

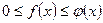Тогда: 1) если 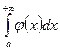сходится, то сходится и 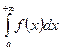, при этом .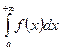

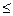
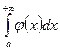2) если 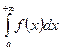расходится, то расходится и .

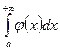2. Если 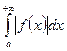сходится, то сходится и .

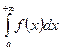Несобственный интеграл 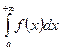называется абсолютно сходящимся, если сходится .

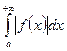Несобственный интеграл 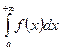называется условно сходящимся, если он сходится, а интеграл 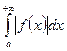расходится.

Пример 8.10. Исследовать сходимость .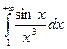

Решение. Заметим, чт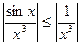о . Но

.

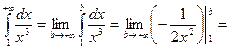
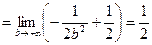Следовательно, 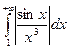сходится. Значит, сходится и .

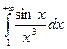8.5.2. Несобственные интегралы второго рода (от неограниченных функций).

Пусть функция 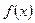определена на промежутке 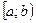, неограниченна на 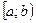, но ограничена на любом промежутке 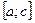, 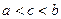. В этом случае точку 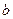называют особой точкой. Предложим также, что 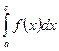существует для любого вещественного числа .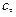

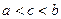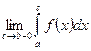называется несобственным интегралом II рода от функции 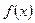на промежутке 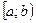и обозначается символом .

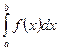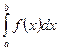
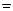
Таким образом, по определению 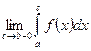(8.19).

Так как вещественное число 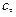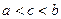, можно представить в ви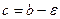де , где 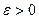, то равенство (8.19) можно записать в виде

.

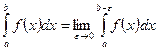Если предел существует и конечен говорят, что несобственный интеграл (8.19) сходится.

В случае, если конечного предела не существует, говорят, что несобственный интеграл расходится.

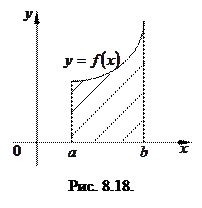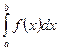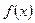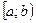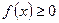
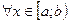Выясним геометрический смысл . Если непрерывна на промежутке и , то 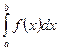есть площадь области, заключенной между осью абсцисс, графиком функции 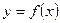и прямым 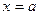и 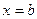(заштрихованная область на рис. 8.18).

Аналогично определяется несобственный интеграл 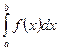, если 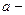особая точка: .

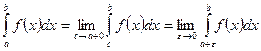Если особой точкой является точка 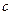внутри промежутка 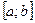, то полагают .

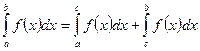При этом считают, что 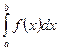сходится, если сходятся оба несобственных интеграла в правой части равенства (8.20) .

Замечания. 1. Понятие несобственного интеграла II рода легко переносится на случай, когда функция 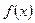имеет конечное число особых точек.

2. Основные выводы п.8.5.1. легко переносятся и на случай несобственных интегралов II рода.

Пример 8.11. Вычислить или доказать расходимость .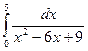

Решение. 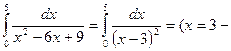точка бесконечного разрыва подынтегральной функции) 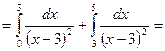(по определению несобственного интеграла второго рода)

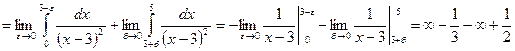. Интеграл расходится.

Пример 8.12. Попробуйте убедиться в том, что 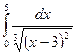сходится.