Основные показатели эффективности инвестиций

Билет 1

1. Эквивалентность платежей: замена одного количества платежей на другое.

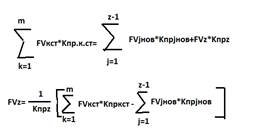
Замена одного количества платежей другим. Если количество платежей по новому договору больше 1, то составляется общее уравнение эквивалентности в котором сумма платежей по старым условиям приведенным по некоторой ….и процентной ставки приравнивается к сумме платежей по новому договору также приведенному к той же дате и %ставке. ∑^м_к=1 FV_кст*Kпр.к.ст=∑^z_j=1FVjнов*kпр.jнов

Для решения этого уравнения в качестве 1-ой из величин, характерны новые условия при заданных прочих, целесообразнее принять размер последнего платежа, который и нужно определить.

2.Средние ставки простых процентов.

При проведении банковских расчетов для удобства изменяют ставки %, заменяют средней. Средняя % ставка- ставка дающая такое наращение, которое эквивалентно наращению с исп ряда разных по значению % ставок; применяют на различных интервалах времени (плавающие ставки %)

Для простых % ср.ставка % опред:

Учетная ставка сложных%:

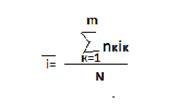
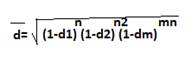
Билет 2

1.Финансовая математика: определения, цели и задачи.

. Фин. вычисления появились с возникновением денег и к сер. 19 века превратились в спец. отрасль знаний, получившую название ком. вычисления или ком. арифметика.

С конца 20 века и до начала 90гг. 20 века в нашей стране применялись методы централизованного рук-ва экономическими процессами, поэтому фин.рычаги не развивались. С переходом к рыночным отношениям потребность в фин.вычислениях вновь резко возросла.

Фин. Математикой – называется совокупность методов определения, изменения стоимости денег, происходящего вследствие их возвратного движения в процессе воспроизводства.

Задачи: 1. Нахождение конечных сумм денежных ср-в, находящихся во вкладах, займах путем начисления %. 2. Учет ц/б. 3. Установление взаимосвязи между отдельными параметрами сделки и определение параметров исходя из заданных условий. 4. Определение эквивалентности параметров сделки для получения равной отдачи от затрат произведенных различными способами. 5. Анализ последствий изменения условий операций. 6. Нахождение обобщающих хар-к и отдельных параметров денежных ср-в. 7.Разработка планов выполнения фин. операций. 8. Расчет показателей доходности фин. операций.

основные параметры: 1. Стоимостные хар-ки (размеры платежей, долговых обяз-в, кредитов и т.д.) 2. Временные данные (даты, сроки выплат, продолжительность льготных периодов, отсрочки платежей). 3. % ставки (иногда задают в открытой форме).

На практике методы фин. мат. Применяют в работе фин. организаций, торговых фирм и инвестиционных компаний, фондовых и валютных бирж.

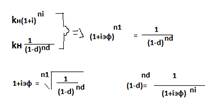
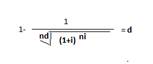
2.Эквивалентность сложных эффективной процентной и учетной ставок.

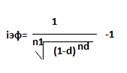
Билет 3*

1. Потребительский кредит: определения и формулы.

Потреб. кредит – это частный случай погашения долга равными срочными уплатами. Самый распространенный способ кредитования населения относится к краткосрочным кредитам. % начисляются по простой ставке на всю сумму долга и присоединяются к сумме в момент выдачи кредита. Погашение производится частями, равномерно в течение всего срока. а) определяем погашенную сумму FV=Д(1+ni), б) определяем стоимость кредита I=FV-Д, в) определяем размер очередного платежа Rp= FV/np. В мировой практике начисление % и выплаты осущ. способом, который называется «метод 78».

Билет 4.*

1)Конверсия рент: замена ренты единовременным платежом.

Конверсия рент-это процесс, связанный с изменением условий рент. Замена ренты единовременным платежом(выкуп ренты)-задача заключается в определении современной величины ренты и сравнением ее с тем единовременным платежом, который задан. Решение проблемы простое. Искомый размер выкупа должен быть равен современной стоимости выкупаемой ренты. Для решения задачи в зависимости от условий погашения задолженности выбирается та или иная формула расчета современной стоимости потока платежей. Естественно, что применяемая при расчете современной стоимости процентная ставка должна удовлетворять обе участвующие стороны. В некоторых случаях ренту с одним набором условий заменяют рентой с другими условиями. При этом конверсия ренты не должна приводить к изменению фин. Последствий для каждой стороны в соглашении, т.е. конверсия ренты должна основываться на принципе фин. эквивалентности платежей. Для того, чтобы провести конверсию ренты, находят ее современную ст-ть, а затем подбирают ренту с такой же современной ст-тью и нужными параметрами.

Билет 5.*

1) Конверсия рент: замена немедленной ренты на отсроченную ренту (n1 = n2).

Конверсия рент-это процесс, связанный с изменением условий рент. Немедленная рента с параметрами R1, n1, i заменяется на отложенную (отсроченную) на t лет с параметрами R2, n2, i

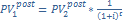, т.е.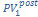

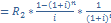
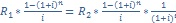отсюда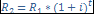

Билет 6.*

1) Обычная финансовая рента: определения, формулы.

Ряд следующих друг за другом выплат и поступлений – это фин. потоки(потоки фин. платежей). Регулярные фин. потоки –это фин. ренты(аннуитеты). В регулярных фин. потоках поступление ср-в осущ-ся через одинаковые промежутки времени(например, взносы от погаш-я кредита, перечисление прибыли…) Член ренты(R)-сумма каждой отдельной выплаты денег, входящей в состав ренты(сумма очередного платежа) . Период ренты-через какие промежутки времени мы платим R. Срок ренты(n)-время от начала фин. ренты до конца последнего ее периода. Доходность ренты( I или j )-это Пс наращенная или дисконтированная. Количество выплат в год(р)- сколько в год мы платим R(если р не равно 1, то R_p).Количество начислений %-ов в год(m).Виды рент: годовые-срочные, дискретные-непрерывные, постоянные-переменные, верные-условные, ограниченные-вечные, немедленные-отложенные, немедленные-отложенные, постнумерандо-пренумерандо.

Постнумерандо(обычная рента)-платежи осущ-ся в конце в конце %-ого периода.

Наращение(определение наращ. суммы)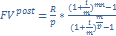

Дисконтирование( современная ст-ть р-срочной ренты)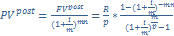

Частные случаи: m=p=1, m=1 p≠1, p=1 m≠1, p=m≠1

Размер очередного платежа и срок как правило определяют из формул постоянной годовой ренты(m=p=1).

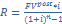( размер год. Платежа)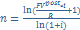

Пренумерандо-платежи производят в начале %-ого периода , отсюда следует, что каждый платеж этой ренты работает на 1 период больше, чем в обычной ренте, и поэтому каждый платеж с начисленными %-ми больше соответствующего показателя обычной ренты в 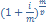раз. Отсюда:

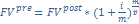
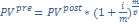
Вечная рента-число членов(сумма каждой отдельной выплаты денег) неограничено. Наращенная сумма при любых параметрах ренты-бесконечно большая(∞). Современная ст-ть: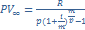

Все ренты объединяет необходимость решений след. Задач: 1) нахождение наращенной суммы, т.е. суммы все платежей с %-ми к концу срока.2)Вычисление современной(приведенной) величины, т.е. сумма все платежей дисконтированных на момент времени, совпадающий с началом потока платежей. 3)На основании 1 и 2 задач вычисление размера очередного платежа или срока ренты.

Билет 7

1. Дисконтирование в условиях инфляции.

Инфляция-снижение покупательной способности денег за конкретный период. Её характеризуют 2 показателя: 1)Индекс цен(индекс инфляции) 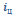-показывает, во сколько раз возросли цены за рассматриваемый период. Это коэффициент. 2)Темп инфляции(γ-гамма), выраженный в %-ах, показывает, на сколько %-ов возросли цены за рассматриваемый период.(уровень инфляции).

Дисконтирование-сложная фин. операция, поэтому в условиях инфляции рассматриваются только ПРОСТЫЕ учетные ставки.

, => ,=> ,=> => ,

* , =>

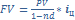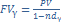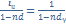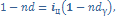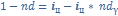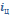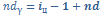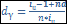
Если n=1год, то 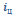=1+ γ, отсюда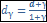

Если n<1 года, то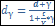

2. Сложные проценты: основные определения и формулы.

Сложными %ами называется метод расчёта дохода кредитора от предоставления денег в долг заёмщику.

Сущность сложных %ов состоит в том, что %ый платёж каждый расчётный период присоединяется к величине капитала предыдущего периода и в последующем рассчитывается с нарощенной величины капитала(% на %)

FV=PV(1+i)ⁿ

FV=PV(1+i)^t/y

a ^m/n =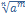

Смешанный метод

Если срок не целое число лет, то формула наращения имеет вид: FV=PV(1+i)^a(1+bi),

Где а – целое число лет, b-дробная часть года

Если ставка сложных % плавающая(переменная), то FV=PV(1+i₁)ⁿ¹(1+i₂)ⁿ²…(1+i_k)^nk

Если % начислен m раз в году, то

FV=PV(1+i/m)^mn

Билет 8

1.Конверсия рент: замена немедленной ренты на немедленную ренту ( n_{1 =} n ₂).

Конверсия ренты – процесс, связанный с изменением условий ренты.

Иногда конверсия ренты заключается в замене ренты единовременным платежем. В некоторых случаях ренту с одним набором условий заменяют рентой с другими условиями. При этом предполагают, что конверсия ренты не должна приводить к изменению финансовых последствий для каждой из участвующих в соглашении сторон, т.е. конверсия ренты должна основываться на принципе финансовой эквивалентности платежей.

Для того чтобы провести конверсию ренты, находят её современную стоимость, а затем подбирают ренту с такой же современной стоимостью и нужными параметрами.

2. Простые проценты: Основные определения и формулы.

Простые %ы-сумма, которую уплачивают за пользование денежными ср-вами. То абсолютная величина D.

%ая ставка-отношение дохода к сумме долга или отношение процентных денег к величине капитала. Относительная величина i,d.

Виды %ых ставок: 1)-обычная, -авансовая ; 2)-фиксированные %, -плавающие % ; 3) –простые %, -сложные % ; 4)-эффективные %, -номинальные % ; 5)-дискретные, -непрерывные.

Период начисления –интервал времени, к которому приурочена(относится)Пс.

Срок начисления-период времени, на протяжении которого действует договор n,t

Простыми %ами называется метод расчёта дохода кредитора от предоставления денег в долг заёмщику.

Сущность простых %ов – состоит в том, что они начисляются на одну и ту же величину капитала в течение всего срока.

Если срок в годах: FV=PV(1+in)

Если срок в днях: FV= PV(1+t/y*i)

Варианты расчетов:

1)английская методика(точные %ы с точным числом дней ссуды) (365/365)

2)французская методика(обыкновенные %ы с точным числом дней в году) (365/360)

3)германская методика(обыкновенные %ы с приближённым числом дней ссуды) (360/360)

Билет 9

1. Конверсия рент: замена немедленной ренты на отсроченную ренту
(R₁ = R₂).

Конверсия ренты – процесс, связанный с изменением условий ренты.

Иногда конверсия ренты заключается в замене ренты единовременным платеже. В некоторых случаях ренту с одним набором условий заменяют рентой с другими условиями. При этом предполагают, что конверсия ренты не должна приводить к изменению финансовых последствий для каждой из участвующих в соглашении сторон, т.е. конверсия ренты должна основываться на принципе финансовой эквивалентности платежей.

Для того чтобы провести конверсию ренты, находят её современную стоимость, а затем подбирают ренту с такой же современной стоимостью и нужными параметрами.

2. Сложные проценты: определения и основные формулы.

Сложными %ами называется метод расчёта дохода кредитора от предоставления денег в долг заёмщику.

Сущность сложных %ов состоит в том, что %ый платёж каждый расчётный период присоединяется к величине капитала предыдущего периода и в последующем рассчитывается с нарощенной величины капитала(% на %)

FV=PV(1+i)ⁿ

FV=PV(1+i)^t/y

a ^m/n =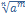

Смешанный метод

Если срок не целое число лет, то формула наращения имеет вид: FV=PV(1+i)^a(1+bi),

Где а – целое число лет, b-дробная часть года

Если ставка сложных % плавающая(переменная), то FV=PV(1+i₁)ⁿ¹(1+i₂)ⁿ²…(1+i_k)^nk

Если % начислен m раз в году, то

FV=PV(1+i/m)^mn

Билет 10*
1) Финансовые ренты: определения, виды, основные параметры.

Основные параметры ренты.

1)Член ренты (размер очередного платежа) – это сумма каждой отдельной выплаты денег, входящей в состав ренты (R) Rp

2)Период ренты – это временные интервалы между двумя платежами

3)срок ренты – время измеренное от начала финансовой ренты до конца последнего ее периода (n)

4) Доходность ренты – это ставка наращения или дисконтирования i(j)

5) кол-во выплат в год – р

6)кол-во начислений % в год – m

Виды рент:
1)Годовые или р-срочные

2)Дискретные или непрерывные

3)Постоянные или переменные

4)Верные(кредиты) или условные (страховка)

5) ограниченные или вечные(число членов которой неограниченно)

6)Немедленная; отсроченная

7)Постнумерандо(обычная,платежи осущ. В конце процентного периода); пренумерандо(если платежи производят в начале процентного периода)

Все ренты объединяет необходимость решения следующих задач 1) Нахождение наращенной суммы, т.е. суммы всех платежей с начисл.% к концу срока.2) вычисление современной величины, т .е суммы всех платежей,дисконтированных на момент времени совпадающих с началом потока платежей 3) На основании первой и второй задачи вычисление размера очередного платежа или срока ренты.

Процесс связанный с изменением условий ренты называют конверсией ренты.Конверсия рент основана на принципе финансовой эквивалентности платежей. Для того чтобы произвести конверсию ренты, находят ее современную стоимость, а затем подбирают ренту с такой же современной стоимостью и нужными параметрами.

Объединение рент- это замена нескольких рент одной. Объединение рент проводят след. Образом: 1)находят современные стоимости рент - слагаемых и суммируют их 2)приравнивают полученную сумму современной стоимости заменяющей ренты 3) задав все параметры заменяющей ренты,кроме одного из уравнения эквивалентности определяют недостающий параметр

Замена ренты разовым платежом (выкуп ренты) Задача заключается в определении современной величины ренты и сравнении ее с тем единовременным платежом который задан.

Замена разового платежа рентой. Рассрочка платежа. Задача состоит в определении одного из параметров R, n,p,m,i при условии, что современная величина и все остальные параметры ренты известны. Современная величина совпадает с размером разового платежа.

Общий случай.Замена ренты с одними условиями на ренту с другими условиями.

Билет 11.*

1) Виды погашений долга и их характеристики.

Кредит или займ в зависимости от условий предусмотренных договором можно погашать единовременным платежом или последовательно во времени путем выплаты равных или неравных сумм. При проведении анализа долгосрочных задолженностей выделяют 3 цели:

1) разработка плана погашений займа адекватным условием финн.договора.

2)оценка стоимости долга с учетом всех поступлений для его погашения и состояние ден.рынка на момент оценивания

3)анализ доходности финансовых операций для кредитора.

В краткосрочных кредитах используется погашение долга единовременным платежом, который включает погашение основной суммы долга и уплаты %. В среднем и долгосрочных кредитах используют погашение частями.

( D- размер кредита,займа,долга; R- размер платежей в погасительный фонд (сразу, частями); ɣ-срочная уплата(ежегодные расходы должника) n – срок,i-ставка процентов по займу; j –ставка процентов погасительного фонда; I- проценты по займу (доход кредитора)

Билет 12*

1)Простые проценты: определение, сущность, основные формулы.

Простыми процентами называется метод расчета дохода кредитора от предоставления денег в долг заемщику. Сущность простых процентов состоит в том что они начисляются на одну и ту же величину капитала в течении всего срока. FV=PV(1+in)-наращенная сумма

FV=PV(1+t/y i) варианты расчетов 1)точные %с точным числом дней (английская практика )

2)обыкновенные проценты с точным числом дней ссуды – французская практика 3)обыкновенные проценты с приближенным числом дней ссуды (германская практика). Если %ставка плавающая то формула имеет вид FV=PV(1+n1i1+n2i2+…+nmim) .капитализация (реинвестирование) процесс повторного инвестирования наращенной суммы по прошествии некоторого периода FV=PV(1+n1i1)(1+n2i2)…(1+nmim)

Билет 13.

1. Погашение единовременным платежом.

Погашение единовременным платежом – предполагает возвращение долга одной суммой. Единовременный платеж характеризуется погасительным фондом и срочной уплатой. Погасительный фонд – накапливаемые на банковском счете средства юр. или физ лиц с целью использования их для погашения ранее взятого кредита. Создание погасительного фонда целесообразно когда j (ставка % погасительного фонда)> i ( ставка % по займу), тогда на счете удается накопить достаточно средств , чтобы на момент погашения кредита была сумма долга с %.Если погасительный фонд создается для уплаты займа, условия которого предусматривают периодическую выплату %, то текущие расходы должника будут состоять из платежа в фонд и выплаты %. Эта сумма называется срочной уплатой(гамма) или расходами заемщика по обслуживанию долга. В этом случае задача разработки плана заключается в определении размера срочной уплаты и составляющих ее элементов в зависимости от конкретных условий. гамма = I + R. Случаи : а)взносы, погашение % и выплаты % по займу осуществляются раз в год. I=D*i ; R= D*j /(1+j)в степени n и минус 1. Гамма = D*j + D*j/(1+j)в степени n и минус 1. FV= гамма *n. D –размер кредита, R – размер платежа в погасительный фонд(единовременным платежом) б) p не равно 1, тогда R = D*p умножить на дробь [(1+j)в степени 1/p и минус 1]- числитель, (1+j)в степени n и минус один – знаменатель. Гамма = D*p умножить на дробь [(1+j)в степени 1/p и минус 1](1+i) в степени n - числитель, (1+j)в степени n и минус один – знаменательв)если процентные суммы присоединяются к основной сумме долга, тогда вычисляют ежегодные расходы . гамма = D*j /(1+j)в степени n и минус 1, и эту дробь умножить на (1+i) в степени n

2. Дисконтирование по ставке сложных процентов

Для того чтобы по известным значениям наращенной суммы , процентной ставки и срока финансовой операции определить современную стоимость применяют дисконтирование. Математическое дисконтирование: PV=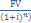

Если проценты начисляют m раз в году то

PV =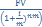

Банковское дисконтирование PV =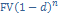

Если дисконтирование проводят по учетной процентной ставке m раз в году то

PV =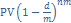

Смешанный метод – если срок нецелое число лет

PV =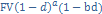

a – целое число лет b – дробная часть года

Билет 14*

Основные показатели эффективности инвестиций.

Финансовый анализ производственных инвестиций заключается в оценивании конечных финансовых результатов инвестиций, т.е. их доходности для инвестора. Эти методы используют на 1-ом этапе изучения привлекательности проекта и при разработке методики измерения эффективности фирмы, ее ресурсах, опыт менеджеров и поэтому каждая из компаний использует свою методику. Но в последнее время сформировались общие подходы в решении данной проблемы. Методики и критерии, применяемые в финансово-экономических расчетах можно разбить на 2 группы:

(1) Дисконтные методы и измерители – это группа учитывает фактор времени. Применяются крупными и средними компаниями.

(2) Бухгалтерские методы и измерители – они без дисконтирования распределенных во времени денежных сумм.

Основные показатели 1-ой группы:

1. Чистый, приведенный доход – обобщенный конечный результат инвестиционной деятельности в абсолютном измерении.

2. Внутренняя норма (уровень доходности) – относительная мера эффективности реализации инвестиционного проекта.

3. Срок окупаемости – характеристика риска, чем больше срок, тем выше вероятность изменения условий для получения ожидаемого дохода.

4. Индекс доходности – отношение доходов к затратам, по своему содержанию близок к показателю рентабельности.

Основные показатели 2-ой группы:

1. Срок окупаемости – в общем смысле он похож на аналогичный показатель первой группы, но время получения доходов не учитывается а доходы не дисконтируются.

2. Отдача капиталовложений –это отношение суммы доходов за весь ожидаемы период отдачи к размеру инвестиций.

3. Удельные капитальные затраты – инвестиционные издержки в расчете на единицу выпуска однородной продукции.

3. Погашение равными суммами в счет долга.

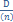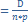В случае если j<I погасительный фонд создавать нецелесообразно и должнику лучше прибегнуть к погашению займа частями. Например , равномерно уплачивая равные суммы в счет долга. В этом случае текущее значение долга с течением времени уменьшается, а следовательно, суммы процентных платежей будут уменьшаться. R = const а)находим размер платежа в счет основного долга R = ; Rp б)определяем сумму % за текущий период ;

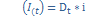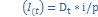
в)определяем остаток долга на начало след.периода ;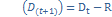

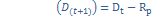
4. Задача: К концу пятилетнего периода необходимо создать фонд 1 млн. руб. Фонд создается равными взносами в конце каждого полугодия. На взносы 2 раза в год начисляются проценты, номинальная ставка равна 60 %. Каков должен быть разовый взнос?

Билет 15.

1. Простые проценты в условиях инфляции: определения, основные формулы.

Инфляцией называется снижение покупательной способности денег за некоторый период. Инфляцию характеризуют 2 показателя: индекс цен (индекс инфляции) – показывает , во сколько раз выросли цены за рассматриваемый период и темп инфляции (гамма) – показывает,на сколько % выросли цены за рассматриваемый период . темп инфляции = индекс цен – 1.Индекс цен и темп инфляции связаны между собой . Если n=1, то индекс цен равен 1 + гамма; индекс цен равен 1+гамма со значком t в степени m,где гамма со значком t =темп инфляции за период менее года(месячный, квартальный) m- количество периодов в году (m=12,2,4 и т.д) Если n>1, то индекс цен = (1+гамма ) в степени n.В задачах темп инфляции задается либо за год, либо за период менее года, индекс инфляции задается за весь рассматриваемый срок . FV со значком гамма = FV*индекс цен. FV гамма = PV(1+ni)*индекс ценили PV (1+t/y *i)*индекс цен. FVгамма = PV(1+n * i с индексом гамма)i с индексом гамма – ставка простых %, в которых заложена инфляция.

2. Эквивалентность простой и сложной номинальной процентных ставок.

=

;

=

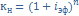
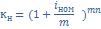
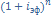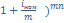
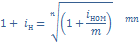
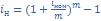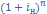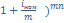
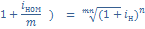
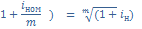
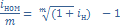
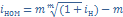
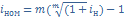
3. Задача: Определить современную величину суммы 3 тыс. руб., которую следует уплатить через 3 года, при дисконтировании по ставке 20 % (сложная учетная).

Билет 16.*

1)Постоянная финансовая рента пренумерандо: определения, основные формулы.

Фин.ренты(аннуитенты)- регулярные фин.потоки.

Поток фин. Платежей- ряд следующих друг за другом выплат и поступлений.

Пренумерандо- когда платежи производятся в начале процентного периода.

1)FV^post = 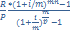PV^post=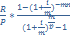

2)Если m=1, p 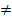1,тогда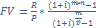

3)Если m=p=1(постоянная годовая),тогда FV= R* 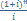; PV=R*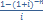

4) Если m 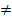1, p=1,тогда FV=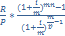

Размер очередного платежа : R=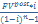

i(j)-доходность ренты; p-кол-во выплат в год; m=кол-во % в год; R-сумма выплаты денег(R_p-менее года)

Билет 17.*

1)Сложные проценты в условиях инфляции: определения, основные формулы.

Инфляция-снижение покупательной способности денег за некоторый период.Характеризуется 2 показателями: 1.индекс цен (i_ц),2.темп инфляции (y_i) ;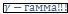

i_ц=(1+i)* ;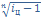

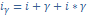
i_ц=m[(1+i/m)* ;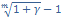

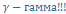
Билет 18.*

1) Вечные ренты: определения и формулы

Фин.ренты(аннуитенты)- регулярные фин.потоки.

Вечная рента – состоит из бесконечно большого количества платежей.

Современная стоимость вечной годовой ренты опр.: PV_∞=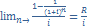

1) m=p=1

Современная стоимость р-срочной вечной ренты с начислением процентов m раз в году:

PV_∞=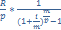

i(j)-доходность ренты; p-кол-во выплат в год; m=кол-во % в год; R-сумма выплаты денег(R_p-менее года)

Билет 19*

1. Срок окупаемости инвестиций.

Срок окупаемости инвестиций - период, в течение которого чистый (дисконтированный) доходстановится положительным. При этом предполагается, что вся отдача от инвестиций представляет собой чистую прибыль. Этот показатель характеризует период времени, в течение которого сделанные инвестором вложения в проект возместятся доходами от его реализации.

Применяют следущие подходы к оценке инвестиционных проектов по сроку окупаемости:

1) проект принимают, если окупаемость имеет место

2) проект принимают только в случае, если срок окупаемости не превышает установленного компанией лимита (например, 5 лет).

Билет 20*

1. Непрерывные проценты.

Уменьшая промежуток времени (год, квартал, месяц, день) до часа (минуты, секунды) и увеличивая частоту начисления процентов, можно перейти к непрерывному наращению процентов.

Непрерывным наращением по ставке i называют увеличение суммы PV в eⁱ раз за один год или в общем случае в eⁱⁿ раз за n лет.

Процентную ставку, применяемую при непрерывном начислении % называют силой роста. Она характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени.

В общем случае формула для расчета непрерывного наращения имеет вид: FV=PV*eⁱⁿ.

Билет 21*

1. Погашение равными срочными уплатами.

Одним из способов погашения долга является погашение равными срочными уплатами, включающими как погашение основной суммы долга, так и выплату процентов.

Припогашении основного долга равными выплатами в конце каждого года выплачивают n-ю долю основного долга: D/n. В конце первого года, крометого, платят % с суммы D, которой пользовались в течение этого года: iD. Основной долг приэтом уменьшится на D/n и составит (D-D/n). В конце второго года выплачивают n-ю долю основного долга:D/n. Кроме того, платят % с суммы D-D/ni, которой пользовались в течение второго года:(D-D/n). Основной долг приэтом уменьшится еще на D/n и составит (D-2D/n) и т.д.

Билет 22. *

1) Погашение равными суммами в счет долга.

В случае, если j < i, R=const; погасительный фонд создавать нецелесообразно и должнику лучше прибегнуть к погашению займа частями, например, равномерно выплачивать равные суммы в счет долга. В этом случае текущее значение долга с течением времени уменьшается, следовательно, суммы процентных платежей также будут уменьшаться.

План погашения долга:

А) находим размер платежа

R=Д/n R_p=Д/n*p

Б) определяем сумму % за текущий период

I_t=Д_t*i I_t=Д_t*(i/p)

В) Определяем остаток долга на начало следующего периода

Д_t+1=Д_t-R Д_t+1=Д_t-R_p

Билет 23. *

1) Виды погашения и их характеристики.

Кредит(займ) в зависимости от условий, предусмотренных договором можно погашать единовременным платежом или последовательно во времени путем выплаты равных и неровных сумм. При проведении анализа долгосрочной задолженности выделяют 3 цели:

1) Разработка плана погашения займа адекватного условия фин.договора.

2) Оценка стоимости долга с учетом всех поступлений для его погашения и состояния денежного рынка на момент оценивания.

3) Анализ доходности фин. Операции для кредитора.

В краткосрочных кредитах используют погашение долга единовременным платежом, который включает погашение основной суммы долга + проценты. В средне- и долгосрочных кредитах используют погашение частями.

Д – долг
R – размер платежа в погасительный фонд, а если частями, то размер платежа.
γ(гамма) – срочная уплата (ежегодные расходы заемщика)
n – срок
i – ставка % по займу
j – ставка % погасительного фонда
I - % по займу.

Билет 24.*

1) Сущность и задачи финансовой математики

Финансовая математике – это наука, изучающая методы и методики определения стоимостных и временных параметров финансовых и инвестиционных операций, процессов и сделок, а также модели управления инвестициями, капиталом и его составляющими.

Объект финансовой математики – финансовые операции и сделки, их технико-экономическое обоснование, направленное на извлечение прибыли.

Предмет финансовой математики – финансовые и актуарные оценки показателей эффективности финансовых операций и сделок, а также доходов отдельно взятых участников этих сделок, определяемых в виде процентных ставок, норм и коэффициентов, скидок, доходов и дивидендов, рент и маржи, котировок ценных бумаг, курсов валют, курсовых разниц и пр.

Финансовая математика охватывает определенный круг методов вычислений, необходимость в которых возникает всякий раз, когда в условиях сделки или финансово-банковской операции оговаривают конкретные значения параметров трех видов:

1) Стоимостные характеристики (размер платежей, долговых обязательств, кредитов и т.д.)

2) Временные данные (даты и сроки выплат, продолжительность льготных периодов, отсрочки платежей и т.д.)

3) Процентные ставки (последние иногда задают в открытой форме)

Билет 25*

1. Переменные ренты: определения, основные формулы.

Ряд следующих друг за другом выплат и поступлений назыв. потоками финансовых платежей. Регулярные финансовые потоки называются финансовыми рентами.

Основные параметры ренты:

1)Сумму каждой отдельной выплаты денег, входящую в состав ренты называют членом ренты (R ). Рентные платежи производятся через равные промежутки времени (Rp)

2) Период ренты – временные интервалы между двумя платежами.

3) Срок ренты - время измеренное от начала фин. ренты до конца последнего ее периода (n).

4) Доходность ренты – это %-ая ставка наращенная или дисконтированная. I,j .

5) Количество выплат в год –p.

6) Количество начислений %-ов в год: m.

Переменные ренты – ренты, параметры которых изменяются во времени.

Суть расчета в этом случае сводится к тому, что если процесс изменения ренты носит несистематический характер и его нельзя описать аналитически, то наращенную и современную стоимости таких потоков следует определять прямым путем, наращивая и дисконтируя к требуемому моменту времени отдельные платежи и затем суммируя полученные результаты.

n

общая формула: PV _f ^post = P₁ + P₂ + ……+ P n = P_k

1+i (1+i)² (1+n)ⁿ (1+i)^k

k=1

P_k - ожидаемое поступление в момент времени K

n - временной горизонт

Билет № 26

1. Вечные ренты: определения, основные формулы.

Ряд следующих друг за другом выплат и поступлений назыв. потоками финансовых платежей. Регулярные финансовые потоки называются финансовыми рентами.

Основные параметры ренты:

1)Сумму каждой отдельной выплаты денег, входящую в состав ренты называют членом ренты (R ). Рентные платежи производятся через равные промежутки времени (Rp)

2) Период ренты – временные интервалы между двумя платежами.

3) Срок ренты - время измеренное от начала фин. ренты до конца последнего ее периода (n).

4) Доходность ренты – это %-ая ставка наращенная или дисконтированная. I,j .

5) Количество выплат в год –p.

6) Количество начислений %-ов в год: m.

Ренту число членов которой неограниченно, называют ВЕЧНОЙ

n ----> ,бесконечность

FV_бескон. = lim FV ^post = lim R * (1+ I )^mn

n à беск. n --- p m_____ -1

-> ,бескон. (1+ I ) _p^m -1

m

PV_бескон = lim PV ^post = lim R * 1 - (1+ I )-^mn =

n à беск. р (1+ I ) _p^m -1

m

= R * ____1________________

р (1+ I ) _p^m -1

m

PV_{бескон =} R

р* (1+ I ) _p^m -1

m

Наращенная сумма вечной ренты при любом ее параметре бесконечно большая величина (ее не находят).

Билет № 27*

1)Погашение долга единовременным платежом

Погашение долга единовременным платежом, предполагает возвращение долга одной суммой.

Единовременный платеж характеризуется погасительным фондом и срочной уплатой.

Погасительный фонд – накапливаемые на банковском счете ср-ва юр. или физ. лиц, с целью использования их для погашения ранее взятого кредита.

Создание погасительного фонда целесообразно, если j=I, тогда на счете удастся накопить достаточно средств, что бы на момент погашения кредита была сумма долга с %.

Если погашенный фонд создается для уплаты займа, условия которого предусматривают периодическую выплату %, то текущие расходы должника будут состоять из платежа в фонд и выплаты % по займу. Эта сумма называется срочной уплатой или расходами заемщика по обслуживанию долга. В этом случае задача разработки плана заключается в определение размера срочной уплаты и составляющих ее элементов, в зависимости от конкретных условий.

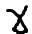=I +R

а) Взносы, погашения % и выплаты % по займу осуществляются один раз в год, тогда:

I = D * i

R = _____D * i______ 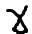= D * I + _____D * i______

(1+j)ⁿ -1 (1+j)ⁿ -1

б) Если платежи в фонд осуществляются р- раз в год, тогда:

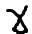R = D_р [ (1 + j) ^1/р - 1] = D_р [ (1 + j) ^1/р - 1] *(1+i)ⁿ

(1+j)ⁿ -1 (1+j)ⁿ -1

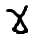в) Если %-ые суммы присоедин. к основоной сумме долга, то вычисляются ежегодные расходы: ____Dj___ * (1+i)ⁿ

= (1+j)ⁿ -1